4.3.3余角与补角2
图片预览

文档简介
(共19张PPT)
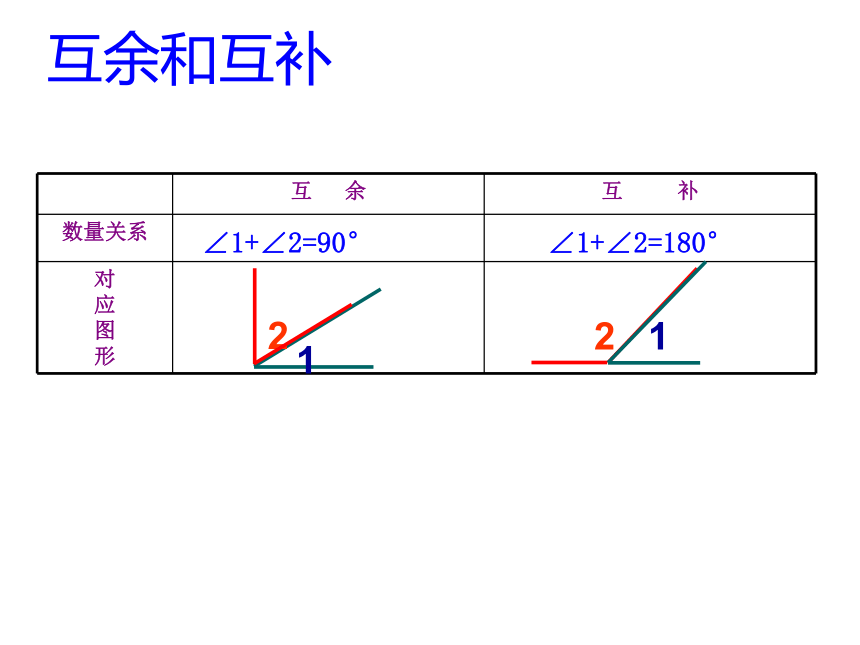
互 余 互 补
数量关系
对
应
图
形
互余和互补
∠1+∠2=90°
∠1+∠2=180°
1
2
2
1
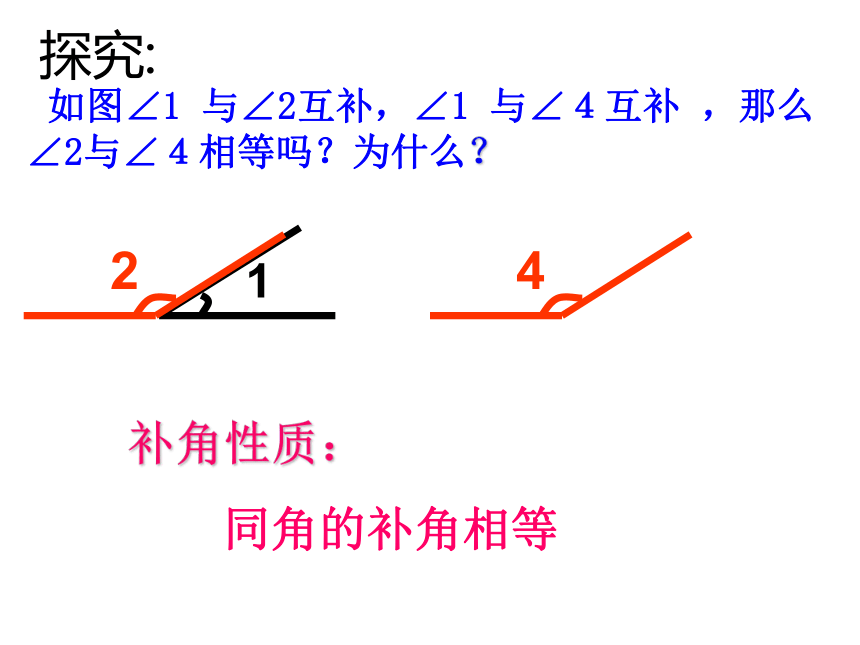
如图∠1 与∠2互补,∠1 与∠4互补 ,那么∠2与∠4相等吗?为什么?
1
2
探究:
4
补角性质:
同角的补角相等
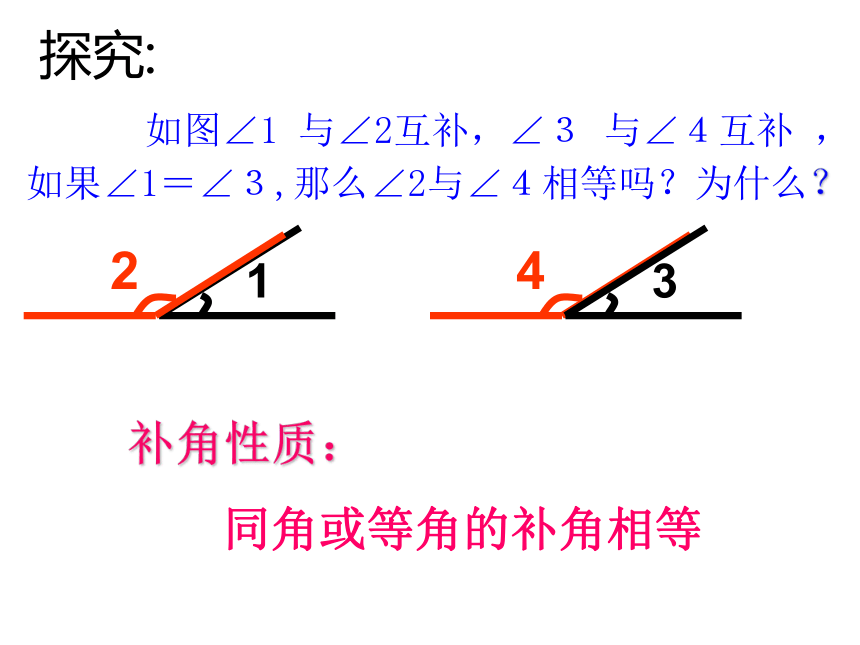
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
探究:
4
3
补角性质:
同角或等角的补角相等
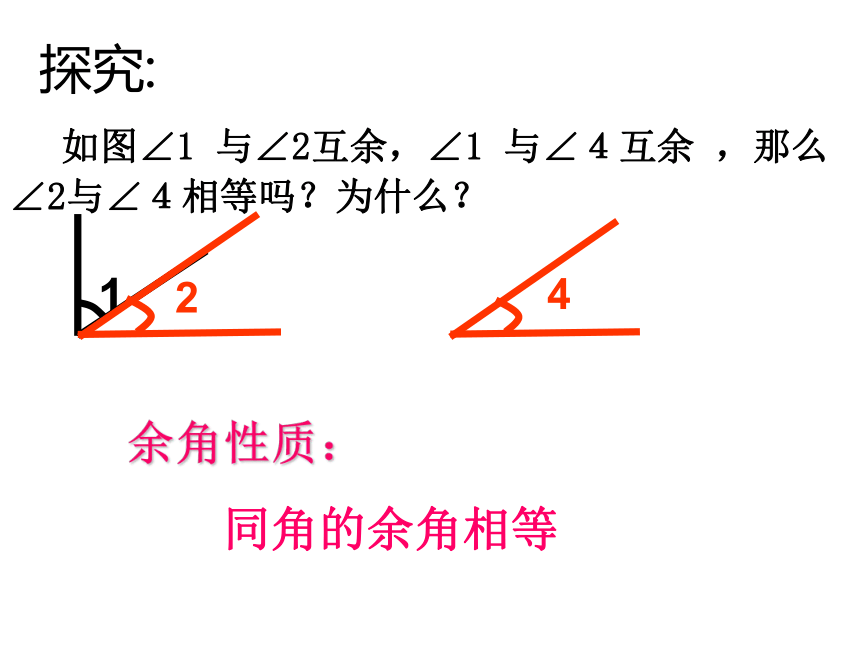
如图∠1 与∠2互余,∠1 与∠4互余 ,那么∠2与∠4相等吗?为什么?
1
2
探究:
4
余角性质:
同角的余角相等
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
探究:
3
4
余角性质:
同角或等角的余角相等
等角的余角相等.
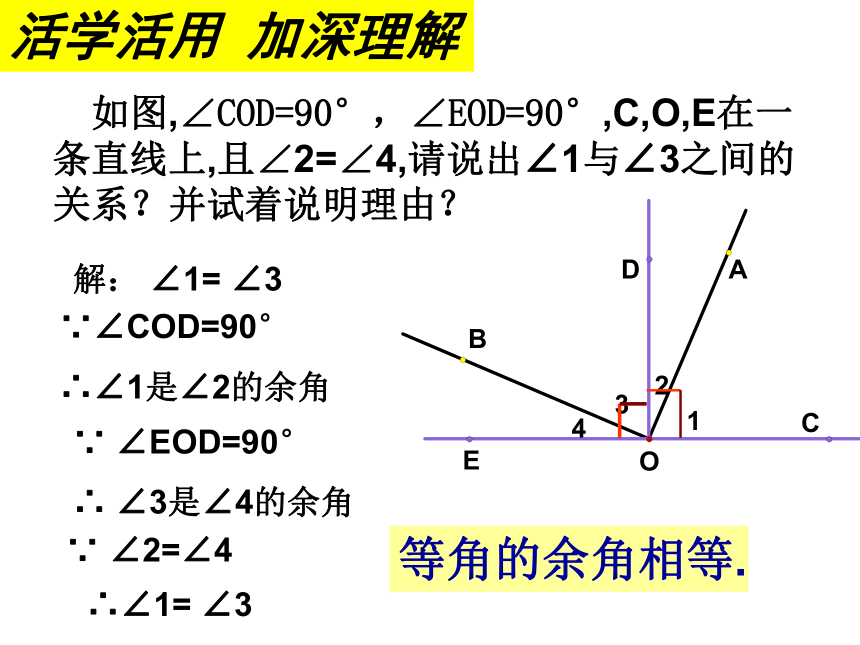
如图,∠COD=90°,∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?
活学活用 加深理解
解: ∠1= ∠3
∵∠COD=90°
∴∠1是∠2的余角
∵ ∠EOD=90°
∴ ∠3是∠4的余角
∵ ∠2=∠4
∴∠1= ∠3
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
OD
45°
北偏西450∠DOE
南偏西450∠BOF
南偏东450∠BOG
北偏东450∠DOH
E
G
F
H
45°
45°
45°
探究:
O
北
南
西
东
(3)南偏西25°
25°
北偏西70°
南偏东60°
A
B
C
∠DOA
∠EOB
∠DOC
70°
60°
D
E
F
G
甲地
乙地
乙地对甲地的方位角
1. 先找出中心点,然后画出方向指标
甲地
乙地
乙地对甲地的方位角
2. 把中心点和目的地用线连接起來
甲地
乙地
乙地对甲地的方位角
3.度量向北的射线和蓝色线之间的角度
北
甲地
乙地
甲地对乙地的方位角
1. 先找出中心点,然后画出方向指标
甲地
乙地
甲地对乙地的方位角
2. 把中心点和目的地用线连接起來
甲地
乙地
甲地对乙地的方位角
3.度量向南的射线和绿色线之间的角度
南
东
西
北
南
●
A
说出B在A的
B
●
40°
70°
●
B
65°
45°
●
B
●
B
那么A在B的
●
B
40°
北偏东40°
南偏西40°
例2:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
∴射线OA的方向就是南偏东60°,即灯塔A所在的方向。
● B
● D
射线OB的方向就是北偏东40°,即客轮B所在的方向。
C ●
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向。
射线OD的方向就是南偏西45°,即海岛D所在的方向。
45°
3、A看B的方向是北偏东30°,那么B看A的方向是( )
(A)南偏东60°(B)南偏西60°
(C)南偏东30° (D)南偏西30°
A
东
北
东
北
1
2
B
互 余 互 补
数量关系
对
应
图
形
互余和互补
∠1+∠2=90°
∠1+∠2=180°
1
2
2
1
如图∠1 与∠2互补,∠1 与∠4互补 ,那么∠2与∠4相等吗?为什么?
1
2
探究:
4
补角性质:
同角的补角相等
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
探究:
4
3
补角性质:
同角或等角的补角相等
如图∠1 与∠2互余,∠1 与∠4互余 ,那么∠2与∠4相等吗?为什么?
1
2
探究:
4
余角性质:
同角的余角相等
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
探究:
3
4
余角性质:
同角或等角的余角相等
等角的余角相等.
如图,∠COD=90°,∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?
活学活用 加深理解
解: ∠1= ∠3
∵∠COD=90°
∴∠1是∠2的余角
∵ ∠EOD=90°
∴ ∠3是∠4的余角
∵ ∠2=∠4
∴∠1= ∠3
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
OD
45°
北偏西450∠DOE
南偏西450∠BOF
南偏东450∠BOG
北偏东450∠DOH
E
G
F
H
45°
45°
45°
探究:
O
北
南
西
东
(3)南偏西25°
25°
北偏西70°
南偏东60°
A
B
C
∠DOA
∠EOB
∠DOC
70°
60°
D
E
F
G
甲地
乙地
乙地对甲地的方位角
1. 先找出中心点,然后画出方向指标
甲地
乙地
乙地对甲地的方位角
2. 把中心点和目的地用线连接起來
甲地
乙地
乙地对甲地的方位角
3.度量向北的射线和蓝色线之间的角度
北
甲地
乙地
甲地对乙地的方位角
1. 先找出中心点,然后画出方向指标
甲地
乙地
甲地对乙地的方位角
2. 把中心点和目的地用线连接起來
甲地
乙地
甲地对乙地的方位角
3.度量向南的射线和绿色线之间的角度
南
东
西
北
南
●
A
说出B在A的
B
●
40°
70°
●
B
65°
45°
●
B
●
B
那么A在B的
●
B
40°
北偏东40°
南偏西40°
例2:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
∴射线OA的方向就是南偏东60°,即灯塔A所在的方向。
● B
● D
射线OB的方向就是北偏东40°,即客轮B所在的方向。
C ●
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向。
射线OD的方向就是南偏西45°,即海岛D所在的方向。
45°
3、A看B的方向是北偏东30°,那么B看A的方向是( )
(A)南偏东60°(B)南偏西60°
(C)南偏东30° (D)南偏西30°
A
东
北
东
北
1
2
B
