北师大版六年级数学上册第7节 圆的面积(二)课件(15张ppt)
文档属性
| 名称 | 北师大版六年级数学上册第7节 圆的面积(二)课件(15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 00:00:00 | ||
图片预览




文档简介
7
圆的面积(二)
一
圆
学习目标
能正确运用圆的面积公式计算圆的面积,并能解决一些简单的实际问题。
在多个探究圆面积公式的活动中,体会圆的半径、直径、周长、面积之间的关系。
学习重难点
应用圆的面积公式解决实际问题。
运用圆的半径、直径、周长、面积之间的关系解决问题。
难点
重点
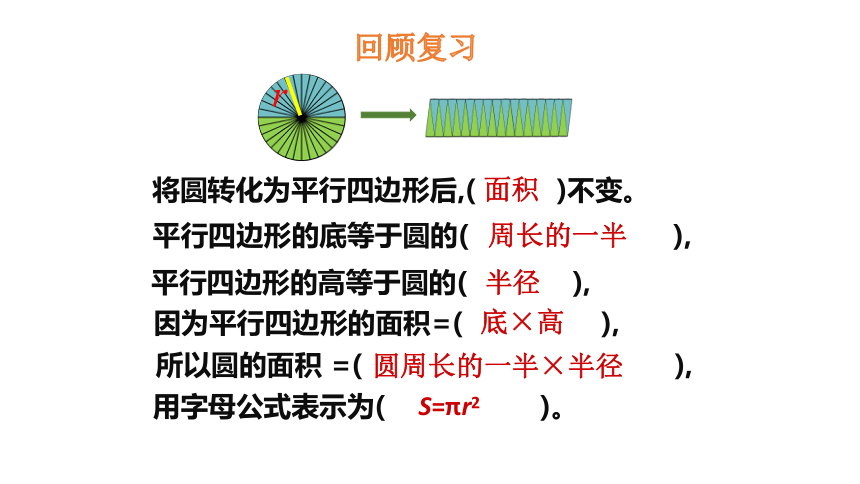
将圆转化为平行四边形后,(
)不变。
回顾复行四边形的底等于圆的(
),
平行四边形的高等于圆的(
),
因为平行四边形的面积=(
),
所以圆的面积
=(
),
用字母公式表示为(
)。
面积
周长的一半
半径
底×高
S=πr2
圆周长的一半×半径
求下面各圆的面积。
????=3.5?cm
?
????=12?cm
?
????=3.14×3.52
?
=38.465(cm2)
?
????=3.14×(12÷2)2
?
=113.04(cm2)
?
????
?
????
?
????=????????????
?
????=????(????÷????)????
?
3.14×32
=3.14×9
=28.26(m2)
答:能浇灌28.26
m2的农田。
喷水半径是3
m,喷水头转动一周,能浇灌多大面积的农田?
3
m
例题解读
已知半径
圆的面积
为????=????????????
?
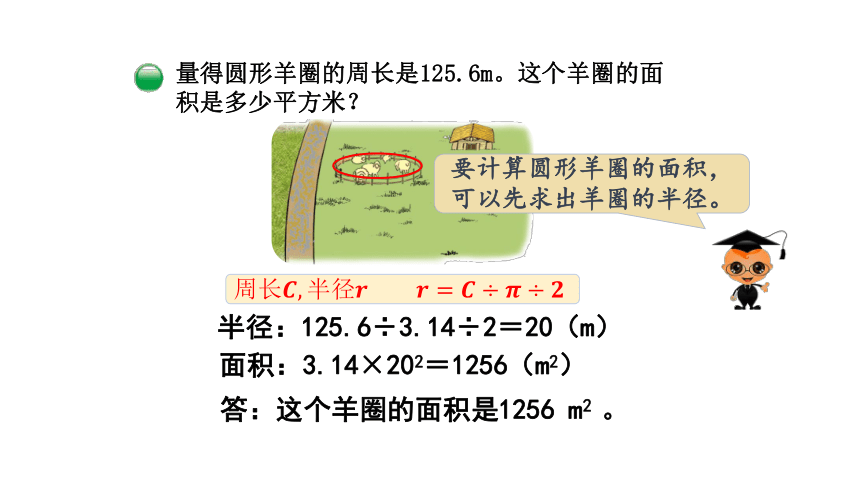
量得圆形羊圈的周长是125.6m。这个羊圈的面积是多少平方米?
半径:125.6÷3.14÷2=20(m)
答:这个羊圈的面积是1256
m2
。
面积:3.14×202=1256(m2)
周长????,半径?????????????????=????÷????÷????
?
要计算圆形羊圈的面积,可以先求出羊圈的半径。
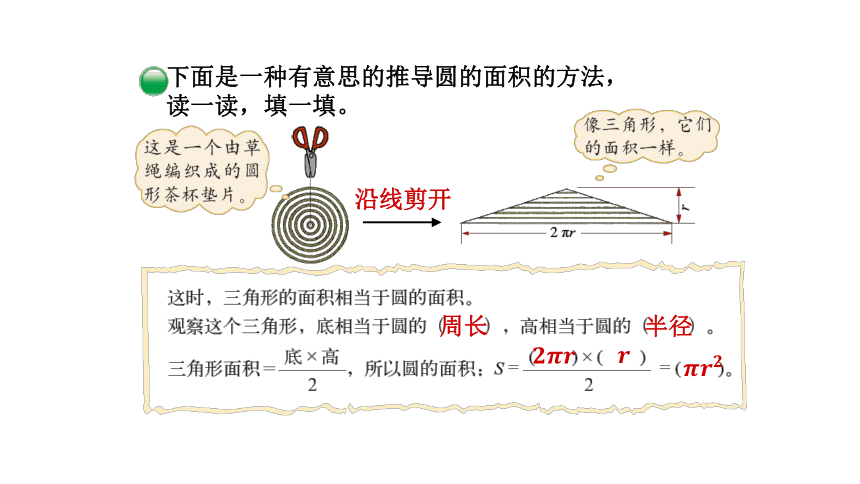
下面是一种有意思的推导圆的面积的方法,读一读,填一填。
沿线剪开
周长
半径
????????????
?
????????????
?
????
?
光盘的银色部分是一个圆环,内圆半径是2
cm,外圆半径是6
cm。圆环的面积是多少?
3.14×62?3.14×22
?
=113.04?12.56
?
=100.48(cm2)
?
外圆面积
内圆面积
规范解答:
圆环的面积=外圆的面积—内圆的面积
方法一
典型例题
圆环的面积=????????(外圆半径??????内圆半径????)
?
方法二
3.14×(62?22)
?
=3.14×32
?
=100.48(cm2)
?
外圆半径的平方-内圆半径的平方
光盘的银色部分是一个圆环,内圆半径是2
cm,外圆半径是6
cm。圆环的面积是多少?
规范解答:
答:圆环的面积是100.48
cm????。
?
小
结
已知圆的周长求面积
????=????????????
????=????(????÷????)????
?
????=??????????????????????=????????????=????(????????????)????
?
圆的面积计算公式
1.
把圆形茶杯垫片沿直径剪开,得到两个近似的三角形,再拼成平行四边形。
????????
?
????
?
????
?
????????
?
????????????
?
随堂小测
2.北京天坛公园的回音壁是闻名世界的声学奇迹,
它是一道圆形围墙。圆的直径约为61.5米,周长
与面积分别是多少?(结果保留一位小数)
周长:3.14×61.5≈193.1(m)
面积:31.4×(61.5÷2)2
≈2969.1(m2)
答:周长约193.1
m。面积约2969.1
m2。
半径????=????????.????÷????=????????.????????(????)
?
3.
下图中的铜钱直径22.5mm,中间的正方形边长为6mm。这个铜钱的面积是多少?
3.14×(22.5÷2)2?6×6
?
=3.14×11.252?36
?
=397.40625?36
?
=361.40625(mm2)
?
答:这个铜钱的面积是361.40625mm2。
?
铜钱的面积=圆的面积—
中间小正方形的面积
4.一个圆形游泳池的半径是50米。在游泳池的四周修一条2米宽的小路。这条小路的面积是多少平方米?
3.14×522?3.14×502
?
答:这条小路的面积是640.56平方米。
游泳池半径50米小路宽2米
圆环外圆半径52米内圆半径50米
求小路面积就是求圆环面积
=640.56(cm2)
?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
圆的面积(二)
一
圆
学习目标
能正确运用圆的面积公式计算圆的面积,并能解决一些简单的实际问题。
在多个探究圆面积公式的活动中,体会圆的半径、直径、周长、面积之间的关系。
学习重难点
应用圆的面积公式解决实际问题。
运用圆的半径、直径、周长、面积之间的关系解决问题。
难点
重点
将圆转化为平行四边形后,(
)不变。
回顾复行四边形的底等于圆的(
),
平行四边形的高等于圆的(
),
因为平行四边形的面积=(
),
所以圆的面积
=(
),
用字母公式表示为(
)。
面积
周长的一半
半径
底×高
S=πr2
圆周长的一半×半径
求下面各圆的面积。
????=3.5?cm
?
????=12?cm
?
????=3.14×3.52
?
=38.465(cm2)
?
????=3.14×(12÷2)2
?
=113.04(cm2)
?
????
?
????
?
????=????????????
?
????=????(????÷????)????
?
3.14×32
=3.14×9
=28.26(m2)
答:能浇灌28.26
m2的农田。
喷水半径是3
m,喷水头转动一周,能浇灌多大面积的农田?
3
m
例题解读
已知半径
圆的面积
为????=????????????
?
量得圆形羊圈的周长是125.6m。这个羊圈的面积是多少平方米?
半径:125.6÷3.14÷2=20(m)
答:这个羊圈的面积是1256
m2
。
面积:3.14×202=1256(m2)
周长????,半径?????????????????=????÷????÷????
?
要计算圆形羊圈的面积,可以先求出羊圈的半径。
下面是一种有意思的推导圆的面积的方法,读一读,填一填。
沿线剪开
周长
半径
????????????
?
????????????
?
????
?
光盘的银色部分是一个圆环,内圆半径是2
cm,外圆半径是6
cm。圆环的面积是多少?
3.14×62?3.14×22
?
=113.04?12.56
?
=100.48(cm2)
?
外圆面积
内圆面积
规范解答:
圆环的面积=外圆的面积—内圆的面积
方法一
典型例题
圆环的面积=????????(外圆半径??????内圆半径????)
?
方法二
3.14×(62?22)
?
=3.14×32
?
=100.48(cm2)
?
外圆半径的平方-内圆半径的平方
光盘的银色部分是一个圆环,内圆半径是2
cm,外圆半径是6
cm。圆环的面积是多少?
规范解答:
答:圆环的面积是100.48
cm????。
?
小
结
已知圆的周长求面积
????=????????????
????=????(????÷????)????
?
????=??????????????????????=????????????=????(????????????)????
?
圆的面积计算公式
1.
把圆形茶杯垫片沿直径剪开,得到两个近似的三角形,再拼成平行四边形。
????????
?
????
?
????
?
????????
?
????????????
?
随堂小测
2.北京天坛公园的回音壁是闻名世界的声学奇迹,
它是一道圆形围墙。圆的直径约为61.5米,周长
与面积分别是多少?(结果保留一位小数)
周长:3.14×61.5≈193.1(m)
面积:31.4×(61.5÷2)2
≈2969.1(m2)
答:周长约193.1
m。面积约2969.1
m2。
半径????=????????.????÷????=????????.????????(????)
?
3.
下图中的铜钱直径22.5mm,中间的正方形边长为6mm。这个铜钱的面积是多少?
3.14×(22.5÷2)2?6×6
?
=3.14×11.252?36
?
=397.40625?36
?
=361.40625(mm2)
?
答:这个铜钱的面积是361.40625mm2。
?
铜钱的面积=圆的面积—
中间小正方形的面积
4.一个圆形游泳池的半径是50米。在游泳池的四周修一条2米宽的小路。这条小路的面积是多少平方米?
3.14×522?3.14×502
?
答:这条小路的面积是640.56平方米。
游泳池半径50米小路宽2米
圆环外圆半径52米内圆半径50米
求小路面积就是求圆环面积
=640.56(cm2)
?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
