人教版物理必修二:第七章 7动能和动能定理
文档属性
| 名称 | 人教版物理必修二:第七章 7动能和动能定理 |

|
|
| 格式 | doc | ||
| 文件大小 | 184.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-08 00:00:00 | ||
图片预览



文档简介
双基限时练(二十) 动能和动能定理
1.两个物体质量比为1:4,速度大小之比为4:1,则这两个物体的动能之比为( )
A.1:1 B.1:4
C.4:1 D.2:1
解析 由动能的表达式Ek=mv2可知C选项正确.
答案 C
2.质量为2 kg的物体A以5 m/s的速度向北运动,另一个质量为0.5 kg的物体B以10 m/s的速度向西运动,则下列说法正确的是( )
A.EkA=EkB
B.EkA>EkB
C.EkAD.因运动方向不同,无法比较动能
解析 动能是标量,没有方向,将各量代入Ek=mv2的表达式,可知A选项正确.
答案 A
3.有两个物体a和b,其质量分别为ma和mb,且ma>mb,它们的动能相同,若a和b分别受到不变的阻力Fa和Fb的作用,经过相同的时间停下来,它们的位移分别为sa和sb,则( )
A.Fa>Fb且saFb且sa>sb
C.Fasb D.Fa解析 由题意知:mav=mbv,由于ma>mb,
所以vasb=t,故得到sa知F=Ek/s,所以Fa>Fb.
答案 A
4.一人用力踢质量为1 kg的皮球,使球由静止以10 m/s的速度飞出,假定人踢球的平均作用力是200 N,球在水平方向运动了20 m停止,那么人对球所做的功为( )
A.50 J B.500 J
C.4 000 J D.无法确定
解析 由动能定理得,人对球做的功W=mv2-0=50 J,故A选项正确.
答案 A
5.一人用力把质量为1 kg的物体由静止向上提高1 m,使物体获得2 m/s的速度,则( )
A.人对物体做的功为12 J
B.合外力对物体做的功为2 J
C.合外力对物体做的功为12 J
D.物体克服重力做的功为10 J
解析 由动能定理得W人-mgh=mv2-0,人对物体做的功为W人=mgh+mv2=1×10×1 J+×1×22 J=12 J,故A项对;合外力做的功W合=mv2=2 J,故B项对,C项错;物体克服重力做功为mgh=10 J,D项对.
答案 ABD
6.质量为M的木块放在光滑的水平面上,质量为m的子弹以速度v0沿水平方向射中木块并最终留在木块中与木块一起以速度v运动.当子弹进入木块的深度为s时相对木块静止,这时木块前进的距离为L.若木块对子弹的阻力大小F视为恒定,下列关系正确的是( )
A.FL=Mv2/2
B.Fs=mv2/2
C.Fs=mv/2-(m+M)v2/2
D.F(L+s)=mv/2-mv2/2
解析 由动能定理得:-F(L+s)=mv2-mv,FL=Mv2,故Fs=-v2,故A、C、D项正确.
答案 ACD
7.一个物体从斜面底端冲上足够长的斜面后又返回到斜面底端,已知物体的初动能为E,它返回到斜面底端的速度为v,克服摩擦力做功为E/2,若物体以2E的初动能冲上斜面,则有( )
A.返回斜面底端时的速度大小为v
B.返回斜面底端时的动能为E
C.返回斜面底端时的动能为
D.物体两次往返克服摩擦力做功相同
解析 由题意可知,第二次初动能是第一次的2倍,两次上滑加速度相同,据推导公式可得s2=2s1,则Wf2=2Wf1=E,回到底端时动能也为E,从而推知返回底端时的速度大小为v.
答案 AB
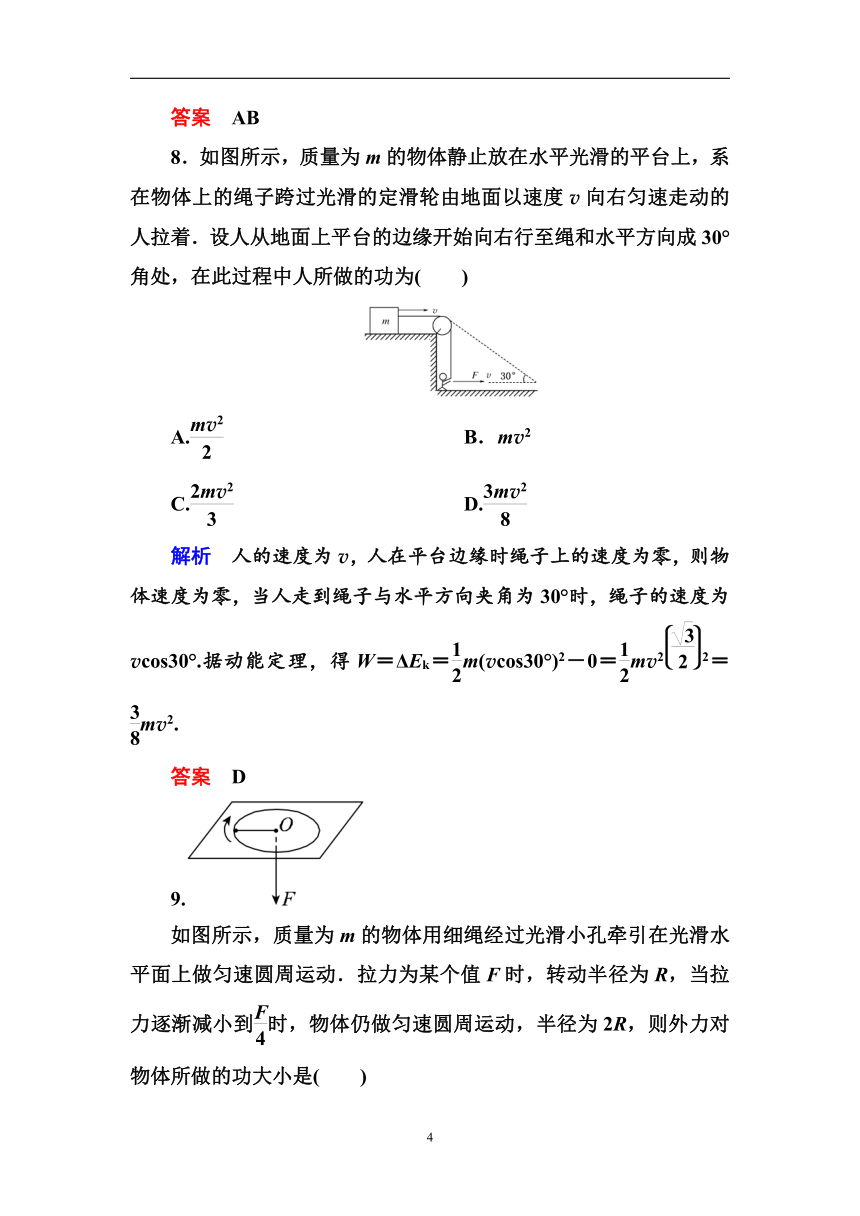
8.如图所示,质量为m的物体静止放在水平光滑的平台上,系在物体上的绳子跨过光滑的定滑轮由地面以速度v向右匀速走动的人拉着.设人从地面上平台的边缘开始向右行至绳和水平方向成30°角处,在此过程中人所做的功为( )
A. B.mv2
C. D.
解析 人的速度为v,人在平台边缘时绳子上的速度为零,则物体速度为零,当人走到绳子与水平方向夹角为30°时,绳子的速度为vcos30°.据动能定理,得W=ΔEk=m(vcos30°)2-0=mv22=mv2.
答案 D
9.
如图所示,质量为m的物体用细绳经过光滑小孔牵引在光滑水平面上做匀速圆周运动.拉力为某个值F时,转动半径为R,当拉力逐渐减小到时,物体仍做匀速圆周运动,半径为2R,则外力对物体所做的功大小是( )
A.0 B.
C. D.
解析 根据拉力提供向心力F=,求得Ek1=FR;当拉力减小到时,有=,求得Ek2=,外力做功数值等于动能的改变量ΔEk=.
答案 C
10.一艘由三个推力相等的发动机驱动的气垫船,在湖面上由静止开始加速前进l距离后关掉一个发动机,气垫船匀速运动,将到码头时,又关掉两个发动机,最后恰好停在码头上,设水给船的阻力大小不变,若船由静止加速前进l距离后三个发动机全部关闭,船通过的距离为多少?
解析 设每个发动机提供的推力为F.由题意可知水的阻力f=2F,加速前进时有(3F-f)l=mv2,
三个发动机都关闭时fl′=mv2,
解得l′=.
答案 l/2
11.
如图所示,物体从高为h的斜面上的A点由静止滑下,在水平面的B点静止.若使其从B点开始运动,再上升到斜面上的A点,需给物体多大的初速度?
解析 对于两个过程运用动能定理列方程求解即可.
物体从A运动到B,
应用动能定理:mgh-W阻=0 ①
物体从B运动到A,设初速度为v,
再应用动能定理:-mgh-W阻=0- ②
由①②两式得:需给物体的初速度为v=2.
答案 2
12.
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点衔接,导轨半径为R,一个质量为m的物块以某一速度向右运动,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,而后向上运动恰能完成半圆周运动到C点,求物块从B到C点克服阻力所做的功?
解析 物块运动到B点,
由于其对导轨的压力为其重力的7倍,
故有:7mg-mg=m,
B点物体的动能为EkB=mv=3mgR,
物块恰好过C点有:mg=m,
C点的动能EkC=mgR.
设物块克服阻力做功为Wf,物块从B点到C点运用动能定理有:-mg·2R-Wf=EkC-EkB=-mgR,
故物块从B点到C点克服阻力所做的功Wf=mgR.
答案 mgR
13.如图所示,倾角θ=37°的斜面底端B平滑连接着半径r=0.40 m的竖直光滑圆轨道.质量m=0.50 kg的小物块,从距地面h=2.7 m处沿斜面由静止开始下滑,小物块与斜面间的动摩擦因数μ=0.25.(sin37°=0.6,cos37°=0.8,取g=10 m/s2)求:
(1)物块滑到斜面底端B时的速度大小;
(2)物块运动到圆轨道的最高点A时,对圆轨道的压力大小.
解析 (1)物块沿斜面下滑到B的过程中,在重力、支持力和摩擦力作用下做匀加速运动,设下滑到斜面底端B时的速度为v,则由动能定理可得:
mgh-μmgcosθ·=mv2-0,
所以v= ,
代入数据解得:v=6.0 m/s.
(2)设物块运动到圆轨道的最高点A时的速度为vA,在A点受到圆轨道的压力为FN.
物块沿圆轨道上滑到A的过程中由动能定理得:
-mg·2r=mv-mv2.
物块运动到圆轨道的最高点A时,
由牛顿第二定律得:FN+mg=m.
由以上两式代入数据解得:FN=20 N.
由牛顿第三定律可知,物块运动到圆轨道的最高点A时,
对圆轨道的压力大小FN′=FN=20 N.
答案 (1)6.0 m/s (2)20 N
1
1.两个物体质量比为1:4,速度大小之比为4:1,则这两个物体的动能之比为( )
A.1:1 B.1:4
C.4:1 D.2:1
解析 由动能的表达式Ek=mv2可知C选项正确.
答案 C
2.质量为2 kg的物体A以5 m/s的速度向北运动,另一个质量为0.5 kg的物体B以10 m/s的速度向西运动,则下列说法正确的是( )
A.EkA=EkB
B.EkA>EkB
C.EkA
解析 动能是标量,没有方向,将各量代入Ek=mv2的表达式,可知A选项正确.
答案 A
3.有两个物体a和b,其质量分别为ma和mb,且ma>mb,它们的动能相同,若a和b分别受到不变的阻力Fa和Fb的作用,经过相同的时间停下来,它们的位移分别为sa和sb,则( )
A.Fa>Fb且sa
C.Fa
所以va
答案 A
4.一人用力踢质量为1 kg的皮球,使球由静止以10 m/s的速度飞出,假定人踢球的平均作用力是200 N,球在水平方向运动了20 m停止,那么人对球所做的功为( )
A.50 J B.500 J
C.4 000 J D.无法确定
解析 由动能定理得,人对球做的功W=mv2-0=50 J,故A选项正确.
答案 A
5.一人用力把质量为1 kg的物体由静止向上提高1 m,使物体获得2 m/s的速度,则( )
A.人对物体做的功为12 J
B.合外力对物体做的功为2 J
C.合外力对物体做的功为12 J
D.物体克服重力做的功为10 J
解析 由动能定理得W人-mgh=mv2-0,人对物体做的功为W人=mgh+mv2=1×10×1 J+×1×22 J=12 J,故A项对;合外力做的功W合=mv2=2 J,故B项对,C项错;物体克服重力做功为mgh=10 J,D项对.
答案 ABD
6.质量为M的木块放在光滑的水平面上,质量为m的子弹以速度v0沿水平方向射中木块并最终留在木块中与木块一起以速度v运动.当子弹进入木块的深度为s时相对木块静止,这时木块前进的距离为L.若木块对子弹的阻力大小F视为恒定,下列关系正确的是( )
A.FL=Mv2/2
B.Fs=mv2/2
C.Fs=mv/2-(m+M)v2/2
D.F(L+s)=mv/2-mv2/2
解析 由动能定理得:-F(L+s)=mv2-mv,FL=Mv2,故Fs=-v2,故A、C、D项正确.
答案 ACD
7.一个物体从斜面底端冲上足够长的斜面后又返回到斜面底端,已知物体的初动能为E,它返回到斜面底端的速度为v,克服摩擦力做功为E/2,若物体以2E的初动能冲上斜面,则有( )
A.返回斜面底端时的速度大小为v
B.返回斜面底端时的动能为E
C.返回斜面底端时的动能为
D.物体两次往返克服摩擦力做功相同
解析 由题意可知,第二次初动能是第一次的2倍,两次上滑加速度相同,据推导公式可得s2=2s1,则Wf2=2Wf1=E,回到底端时动能也为E,从而推知返回底端时的速度大小为v.
答案 AB
8.如图所示,质量为m的物体静止放在水平光滑的平台上,系在物体上的绳子跨过光滑的定滑轮由地面以速度v向右匀速走动的人拉着.设人从地面上平台的边缘开始向右行至绳和水平方向成30°角处,在此过程中人所做的功为( )
A. B.mv2
C. D.
解析 人的速度为v,人在平台边缘时绳子上的速度为零,则物体速度为零,当人走到绳子与水平方向夹角为30°时,绳子的速度为vcos30°.据动能定理,得W=ΔEk=m(vcos30°)2-0=mv22=mv2.
答案 D
9.
如图所示,质量为m的物体用细绳经过光滑小孔牵引在光滑水平面上做匀速圆周运动.拉力为某个值F时,转动半径为R,当拉力逐渐减小到时,物体仍做匀速圆周运动,半径为2R,则外力对物体所做的功大小是( )
A.0 B.
C. D.
解析 根据拉力提供向心力F=,求得Ek1=FR;当拉力减小到时,有=,求得Ek2=,外力做功数值等于动能的改变量ΔEk=.
答案 C
10.一艘由三个推力相等的发动机驱动的气垫船,在湖面上由静止开始加速前进l距离后关掉一个发动机,气垫船匀速运动,将到码头时,又关掉两个发动机,最后恰好停在码头上,设水给船的阻力大小不变,若船由静止加速前进l距离后三个发动机全部关闭,船通过的距离为多少?
解析 设每个发动机提供的推力为F.由题意可知水的阻力f=2F,加速前进时有(3F-f)l=mv2,
三个发动机都关闭时fl′=mv2,
解得l′=.
答案 l/2
11.
如图所示,物体从高为h的斜面上的A点由静止滑下,在水平面的B点静止.若使其从B点开始运动,再上升到斜面上的A点,需给物体多大的初速度?
解析 对于两个过程运用动能定理列方程求解即可.
物体从A运动到B,
应用动能定理:mgh-W阻=0 ①
物体从B运动到A,设初速度为v,
再应用动能定理:-mgh-W阻=0- ②
由①②两式得:需给物体的初速度为v=2.
答案 2
12.
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点衔接,导轨半径为R,一个质量为m的物块以某一速度向右运动,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,而后向上运动恰能完成半圆周运动到C点,求物块从B到C点克服阻力所做的功?
解析 物块运动到B点,
由于其对导轨的压力为其重力的7倍,
故有:7mg-mg=m,
B点物体的动能为EkB=mv=3mgR,
物块恰好过C点有:mg=m,
C点的动能EkC=mgR.
设物块克服阻力做功为Wf,物块从B点到C点运用动能定理有:-mg·2R-Wf=EkC-EkB=-mgR,
故物块从B点到C点克服阻力所做的功Wf=mgR.
答案 mgR
13.如图所示,倾角θ=37°的斜面底端B平滑连接着半径r=0.40 m的竖直光滑圆轨道.质量m=0.50 kg的小物块,从距地面h=2.7 m处沿斜面由静止开始下滑,小物块与斜面间的动摩擦因数μ=0.25.(sin37°=0.6,cos37°=0.8,取g=10 m/s2)求:
(1)物块滑到斜面底端B时的速度大小;
(2)物块运动到圆轨道的最高点A时,对圆轨道的压力大小.
解析 (1)物块沿斜面下滑到B的过程中,在重力、支持力和摩擦力作用下做匀加速运动,设下滑到斜面底端B时的速度为v,则由动能定理可得:
mgh-μmgcosθ·=mv2-0,
所以v= ,
代入数据解得:v=6.0 m/s.
(2)设物块运动到圆轨道的最高点A时的速度为vA,在A点受到圆轨道的压力为FN.
物块沿圆轨道上滑到A的过程中由动能定理得:
-mg·2r=mv-mv2.
物块运动到圆轨道的最高点A时,
由牛顿第二定律得:FN+mg=m.
由以上两式代入数据解得:FN=20 N.
由牛顿第三定律可知,物块运动到圆轨道的最高点A时,
对圆轨道的压力大小FN′=FN=20 N.
答案 (1)6.0 m/s (2)20 N
1
