北师大版八年级数学上册1.1 探索勾股定理课件 (共22张PPT)
文档属性
| 名称 | 北师大版八年级数学上册1.1 探索勾股定理课件 (共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 23:12:34 | ||
图片预览

文档简介
(共22张PPT)
1.1
探索勾股定理
北师大版八年级数学上册
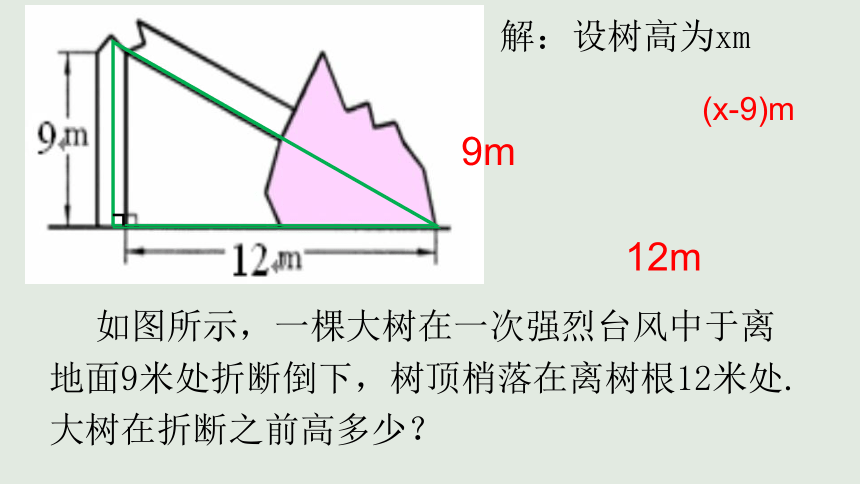
如图所示,一棵大树在一次强烈台风中于离地面9米处折断倒下,树顶梢落在离树根12米处.大树在折断之前高多少?
12m
9m
(x-9)m
解:设树高为xm
┓
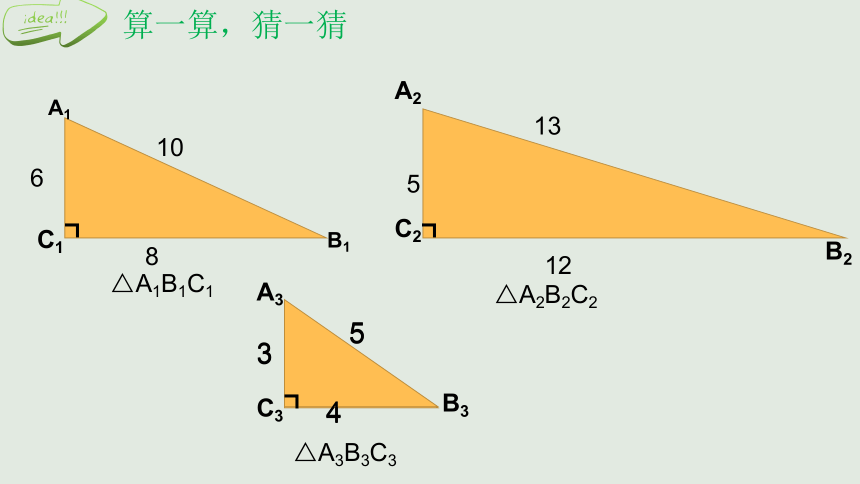
算一算,猜一猜
6
8
10
5
12
13
△A1B1C1
3
4
5
△A3B3C3
△A2B2C2
3
4
5
A2
B2
C2
B3
A3
C3
┓
┓
┓
A1
B1
C1
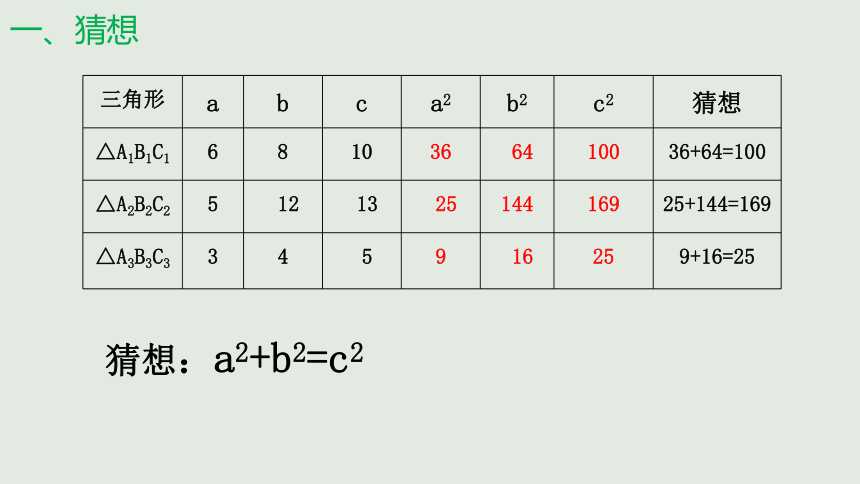
三角形
a
b
c
a2
b2
c2
猜想
△A1B1C1
6
8
10
36
64
100
36+64=100
△A2B2C2
5
12
13
25
144
169
25+144=169
△A3B3C3
3
4
5
9
16
25
9+16=25
猜想:a2+b2=c2
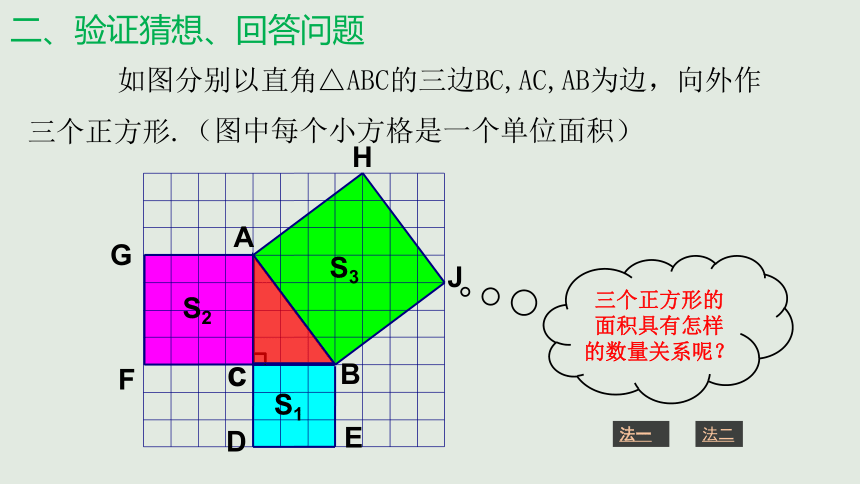
一、猜想
如图分别以直角△ABC的三边BC,AC,AB为边,向外作三个正方形.
C
B
A
c
(图中每个小方格是一个单位面积)
三个正方形的面积具有怎样的数量关系呢?
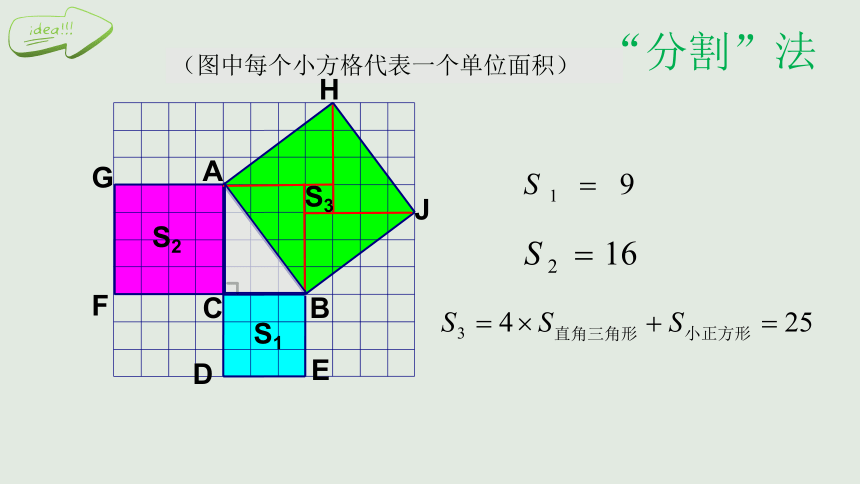
S1
S2
S3
D
E
F
G
H
J
二、验证猜想、回答问题
法一
法二
C
A
B
C
S1
S2
S3
(图中每个小方格代表一个单位面积)
D
E
F
G
H
J
“分割”法
C
A
B
C
S1
S2
S3
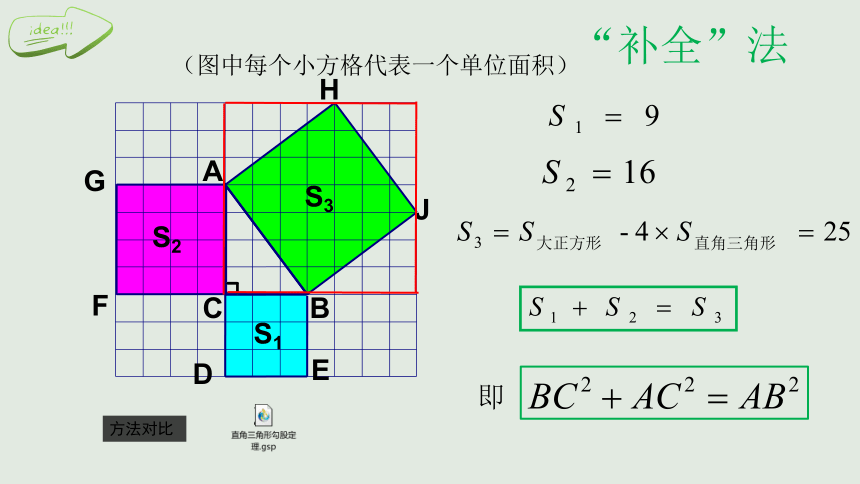
即
(图中每个小方格代表一个单位面积)
D
E
F
G
H
J
“补全”法
方法对比
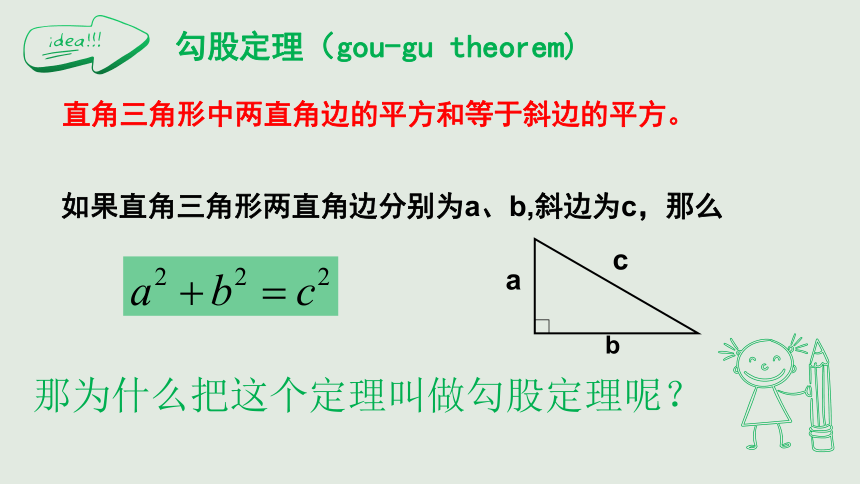
勾股定理(gou-gu
theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
直角三角形中两直角边的平方和等于斜边的平方。
那为什么把这个定理叫做勾股定理呢?
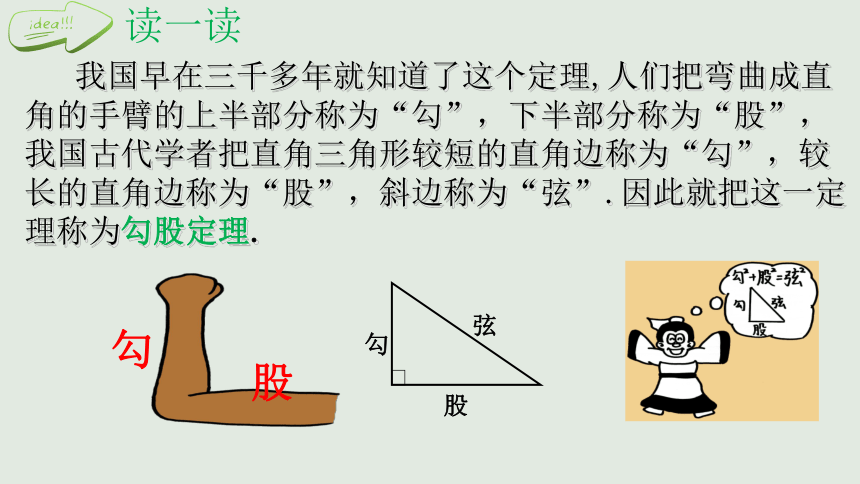
勾
股
勾
股
弦
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
读一读
“分割”法:将一个不易计算的图形分割成易于计算的图形.
“补全”法:将一个不易计算的图形补全成易于计算的图形,再减去多余的部分.
分割法和补全法是几何问题中计算面积体积最常用的两种方法。
c
a
b
1、拿出准备好的四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,
斜边为c);
2、你能用这四个直角三角形拼成一个正方形吗?
3、你能否就你拼出的图证明a2+b2=c2?
拼一拼,证一证
方法
1
方法
2
方法
3
c
赵爽弦图
大正方形的面积可以表示为
也可以表示为
c2
a
b
c
a
b
邹元治证法
大正方形的面积为
也可以表示为
(a+b)2
总统证法
a
D
b
C
c
a
b
c
A
B
E
又
比较两式可知:a2+b2=c2
1876年,美国总统伽菲尔德利用上图验证了勾股定理,人们为了纪念他对勾股定理的证明,就把这一证法称为
“总统证法”
相传两千五百多年前,一次毕达哥拉斯去朋友家做客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系!
发现了什么?
如图所示,一棵大树在一次强烈台风中于离地面9米处折断倒下,树梢顶落在离树根12米处.大树在折断之前高多少?
12m
9m
(x-9)m
解:设树高为xm
┓
┓
┓
12m
9m
(x-9)m
解:设树高为xm
由题可知:81+144=(x-9)2
∴225=(x-9)2
∴x-9=15或x-9=-15(舍)
∴x=24
答:树高为24m.
练一练
1.在△ABC中,∠C=90°,若AB=10,
BC=6,那么AC2为
练一练
练一练
几何问题要利用图形来解决问题
A
B
C
10
6
练一练
A
B
C
10
6
A
B
C
10
6
分类讨论思想
练一练
练一练
2
.在Rt△ABC中,若AB=10,
BC=6,那么AC2为
解:若AB,BC为直角边,AC为斜边
∴AC2=AB2+BC2=136.
若AB为斜边,BC,AC为直角边
∴AC2=AB2-BC2=64.
综上,AC2值为136或64.
Rt△ABC中,∠C=90?,
a2+b2=c2
数、形连接的桥梁
忆一忆
分类讨论思想
thanks
1.1
探索勾股定理
北师大版八年级数学上册
如图所示,一棵大树在一次强烈台风中于离地面9米处折断倒下,树顶梢落在离树根12米处.大树在折断之前高多少?
12m
9m
(x-9)m
解:设树高为xm
┓
算一算,猜一猜
6
8
10
5
12
13
△A1B1C1
3
4
5
△A3B3C3
△A2B2C2
3
4
5
A2
B2
C2
B3
A3
C3
┓
┓
┓
A1
B1
C1
三角形
a
b
c
a2
b2
c2
猜想
△A1B1C1
6
8
10
36
64
100
36+64=100
△A2B2C2
5
12
13
25
144
169
25+144=169
△A3B3C3
3
4
5
9
16
25
9+16=25
猜想:a2+b2=c2
一、猜想
如图分别以直角△ABC的三边BC,AC,AB为边,向外作三个正方形.
C
B
A
c
(图中每个小方格是一个单位面积)
三个正方形的面积具有怎样的数量关系呢?
S1
S2
S3
D
E
F
G
H
J
二、验证猜想、回答问题
法一
法二
C
A
B
C
S1
S2
S3
(图中每个小方格代表一个单位面积)
D
E
F
G
H
J
“分割”法
C
A
B
C
S1
S2
S3
即
(图中每个小方格代表一个单位面积)
D
E
F
G
H
J
“补全”法
方法对比
勾股定理(gou-gu
theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
直角三角形中两直角边的平方和等于斜边的平方。
那为什么把这个定理叫做勾股定理呢?
勾
股
勾
股
弦
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
读一读
“分割”法:将一个不易计算的图形分割成易于计算的图形.
“补全”法:将一个不易计算的图形补全成易于计算的图形,再减去多余的部分.
分割法和补全法是几何问题中计算面积体积最常用的两种方法。
c
a
b
1、拿出准备好的四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,
斜边为c);
2、你能用这四个直角三角形拼成一个正方形吗?
3、你能否就你拼出的图证明a2+b2=c2?
拼一拼,证一证
方法
1
方法
2
方法
3
c
赵爽弦图
大正方形的面积可以表示为
也可以表示为
c2
a
b
c
a
b
邹元治证法
大正方形的面积为
也可以表示为
(a+b)2
总统证法
a
D
b
C
c
a
b
c
A
B
E
又
比较两式可知:a2+b2=c2
1876年,美国总统伽菲尔德利用上图验证了勾股定理,人们为了纪念他对勾股定理的证明,就把这一证法称为
“总统证法”
相传两千五百多年前,一次毕达哥拉斯去朋友家做客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系!
发现了什么?
如图所示,一棵大树在一次强烈台风中于离地面9米处折断倒下,树梢顶落在离树根12米处.大树在折断之前高多少?
12m
9m
(x-9)m
解:设树高为xm
┓
┓
┓
12m
9m
(x-9)m
解:设树高为xm
由题可知:81+144=(x-9)2
∴225=(x-9)2
∴x-9=15或x-9=-15(舍)
∴x=24
答:树高为24m.
练一练
1.在△ABC中,∠C=90°,若AB=10,
BC=6,那么AC2为
练一练
练一练
几何问题要利用图形来解决问题
A
B
C
10
6
练一练
A
B
C
10
6
A
B
C
10
6
分类讨论思想
练一练
练一练
2
.在Rt△ABC中,若AB=10,
BC=6,那么AC2为
解:若AB,BC为直角边,AC为斜边
∴AC2=AB2+BC2=136.
若AB为斜边,BC,AC为直角边
∴AC2=AB2-BC2=64.
综上,AC2值为136或64.
Rt△ABC中,∠C=90?,
a2+b2=c2
数、形连接的桥梁
忆一忆
分类讨论思想
thanks
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
