沪科版数学九年级上册22.4图形的位似变换课件(共17张PPT)
文档属性
| 名称 | 沪科版数学九年级上册22.4图形的位似变换课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
平面直角坐标系中图形的位似变换
沪科版九年级数学上册
D
E
F
A
O
B
C
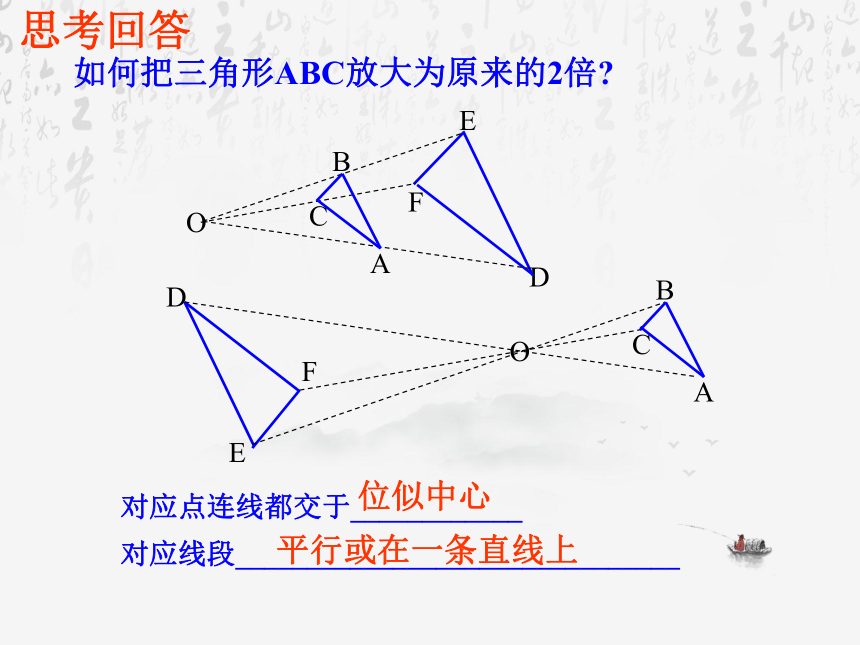
如何把三角形ABC放大为原来的2倍?
D
E
F
A
O
B
C
对应点连线都交于____________
对应线段_______________________________
位似中心
平行或在一条直线上
思考回答
1、如果把位似图形放到平面直角坐标系中,又如何去探究位似变换与坐标之间的关系呢?
接下来想一想?
B'
A'
x
y
B
A
o
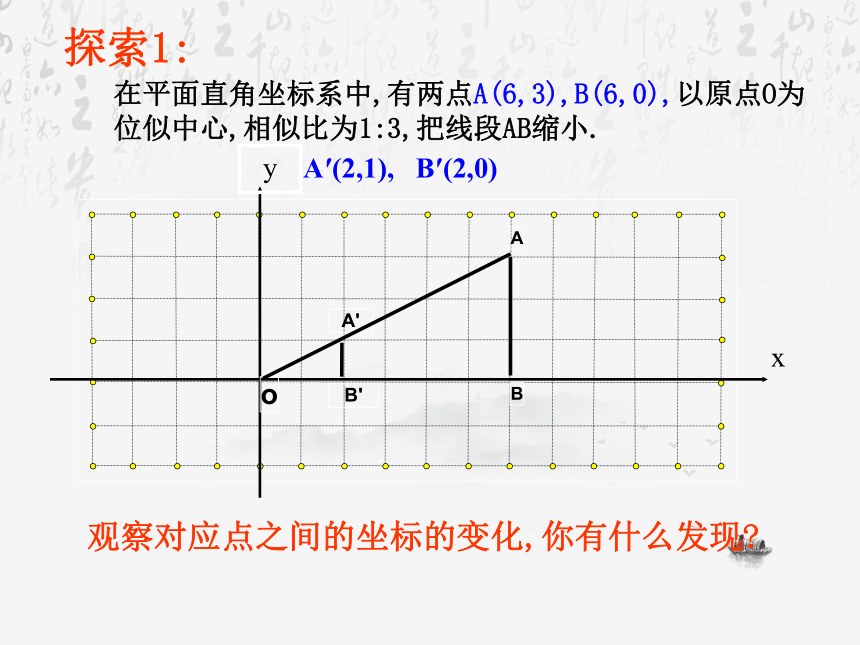
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),
B′(2,0)
观察对应点之间的坐标的变化,你有什么发现?
探索1:
B'
A'
x
y
B
A
o
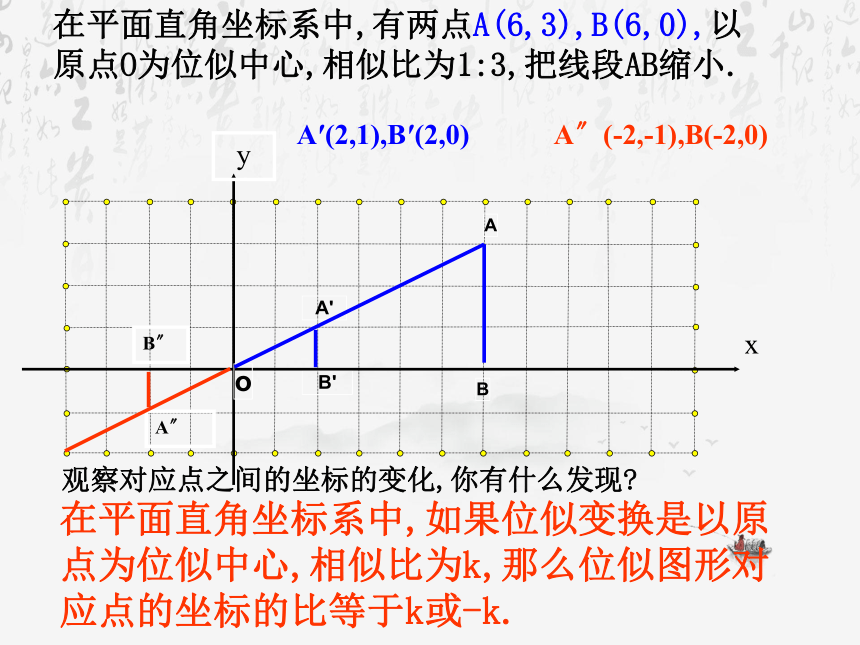
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0)
A〞
B〞
A〞(-2,-1),B(-2,0)
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
观察对应点之间的坐标的变化,你有什么发现?
x
y
o
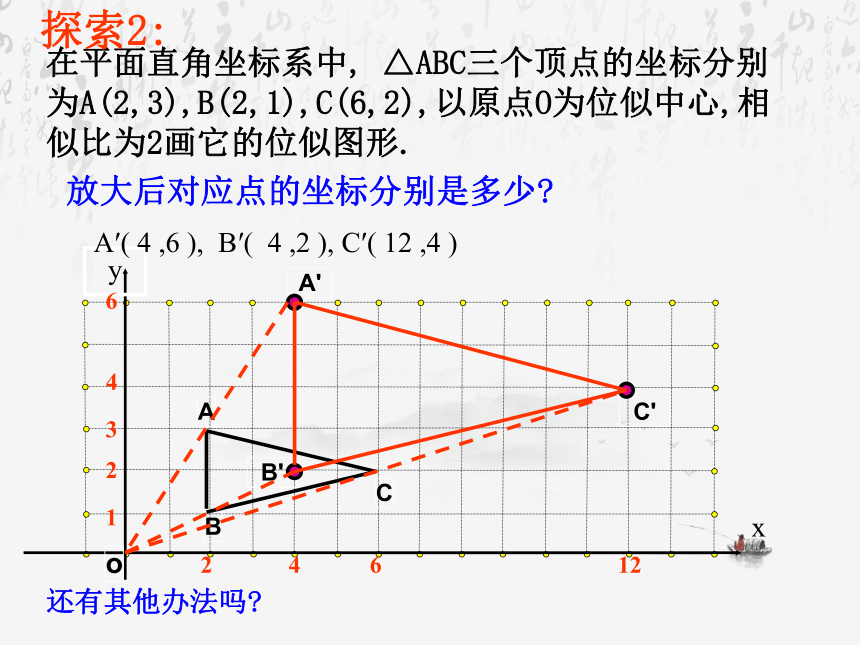
在平面直角坐标系中,
△ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2画它的位似图形.
B
A
C
A′(
4
,6
),
B′(
4
,2
),
C′(
12
,4
)
放大后对应点的坐标分别是多少?
B'
A'
C'
探索2:
还有其他办法吗?
2
4
6
12
1
3
6
2
4
x
y
o
在平面直角坐标系中,
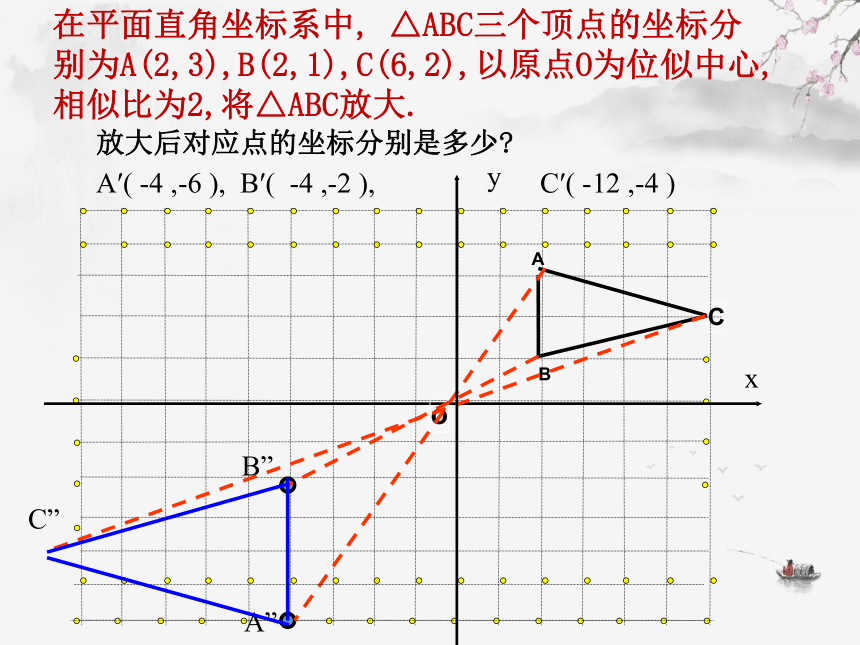
△ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,将△ABC放大.
A′(
-4
,-6
),
B′(
-4
,-2
),
C′(
-12
,-4
)
B
A
C
放大后对应点的坐标分别是多少?
B”
A”
C”
x
y
o
例题1.在平面直角坐标系中,
四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.
A′(
-3,3
),
B′(
-4,1
),
C′(
-2,0
),
D′(
-1,2
)
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗?试试看.
探索3
整个图形形状不变,大小扩大2倍后,对应的坐标又有什么变化呢?
x
y
0
(5,4)
(x,y)?(2x,2y)
探索4
将图中的鱼横向伸长到原来的2倍,那么它的坐标将会发生什么变化呢?
x
y
0
A’(10,4)
D'
C’
E’(8,-2)
B’
E(4,-2)
A(5,4)
D(5,-1)
C(5,1)
B(3,0)
纵坐标保持不变,横坐标分别变成原来的2倍.
87654321
-1
-2
-3
-4
y
0
1
2
3
4
5
6
7
8
9
10
x
图形被横向压缩为原来的1/2
–4
1
2
3
4
5
6
7
8
0
–1
–2
–3
6
1
2
3
4
5
7
8
9
10
x
y
原图形被纵向拉伸到原来的2倍
在平面直角坐标系中,在作(x,y)
?
(x,ay)或(ax,y)变换时,
这不是相似变换,叫伸缩变换。
x
y
o
B
1.如图表示△AOB和把它缩小后得到的△COD,求它们的相似比
A
C
D
练一练:
x
y
o
2.如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.所得三角形的三个顶点坐标分别是多少?
B
A
C
练一练:
位似变换中对应点的坐标的变化规律:
在平面直角坐标系中,如果位似变换是以原点为位似中心相似比为k,那么位似图形对应点的坐标为ka或-ka,a为原顶点的横纵坐标.
如:在以O为原点的坐标系内,△ABC的顶点坐标分别为A(1,1)、B(2,3)、C(4,2),若以O为位似中心在△ABC同侧放大,相似比为2,则A’坐标为(2,2)、B’(4,6)、C’(8,4);若以O为位似中心在△ABC异侧放大,相似比为2,则A’’(-2,-3)、B’’(-4,-6)、C’’(-8、-4)
在平面直角坐标系中,如果位似变换是以三角形的一个靠近原点的顶点为位似中心,相似比为k,那么位似图形对应点的坐标变成ka-(k-1)或-ka+(k+1),a为原顶点的横纵坐标.
如:在以O为原点的坐标系内,△ABC的顶点坐标分别为A(1,1)、B(2,3)、C(4,2),若以A为位似中心在△ABC同侧放大,相似比为2,则A’坐标为(1,1)、B’(3,5)、C’(7,3);若以O为位似中心在△ABC异侧放大,相似比为2,则A’’(1,1)、B’’(-1,-3)、C’’(-5、-1)。
课堂小结:
1、如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,
那么这样的两个图形叫做 。
2、
这个点叫做 。
3、这时的相似比又称为
。
4、位似图形上任意一对对应点到位似中
心的距离之比等于
。
5.
在以坐标原点为位似中心的位似变换中若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为
(kx,ky)或(―kx,―ky)
6、在平面直角坐标系中在作(x,y)
?
(x,ay)或(ax,y)变换时,
叫伸缩变换。
位似图形
位似中心
位似比
位似比
平面直角坐标系中图形的位似变换
沪科版九年级数学上册
D
E
F
A
O
B
C
如何把三角形ABC放大为原来的2倍?
D
E
F
A
O
B
C
对应点连线都交于____________
对应线段_______________________________
位似中心
平行或在一条直线上
思考回答
1、如果把位似图形放到平面直角坐标系中,又如何去探究位似变换与坐标之间的关系呢?
接下来想一想?
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),
B′(2,0)
观察对应点之间的坐标的变化,你有什么发现?
探索1:
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0)
A〞
B〞
A〞(-2,-1),B(-2,0)
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
观察对应点之间的坐标的变化,你有什么发现?
x
y
o
在平面直角坐标系中,
△ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2画它的位似图形.
B
A
C
A′(
4
,6
),
B′(
4
,2
),
C′(
12
,4
)
放大后对应点的坐标分别是多少?
B'
A'
C'
探索2:
还有其他办法吗?
2
4
6
12
1
3
6
2
4
x
y
o
在平面直角坐标系中,
△ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,将△ABC放大.
A′(
-4
,-6
),
B′(
-4
,-2
),
C′(
-12
,-4
)
B
A
C
放大后对应点的坐标分别是多少?
B”
A”
C”
x
y
o
例题1.在平面直角坐标系中,
四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.
A′(
-3,3
),
B′(
-4,1
),
C′(
-2,0
),
D′(
-1,2
)
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗?试试看.
探索3
整个图形形状不变,大小扩大2倍后,对应的坐标又有什么变化呢?
x
y
0
(5,4)
(x,y)?(2x,2y)
探索4
将图中的鱼横向伸长到原来的2倍,那么它的坐标将会发生什么变化呢?
x
y
0
A’(10,4)
D'
C’
E’(8,-2)
B’
E(4,-2)
A(5,4)
D(5,-1)
C(5,1)
B(3,0)
纵坐标保持不变,横坐标分别变成原来的2倍.
87654321
-1
-2
-3
-4
y
0
1
2
3
4
5
6
7
8
9
10
x
图形被横向压缩为原来的1/2
–4
1
2
3
4
5
6
7
8
0
–1
–2
–3
6
1
2
3
4
5
7
8
9
10
x
y
原图形被纵向拉伸到原来的2倍
在平面直角坐标系中,在作(x,y)
?
(x,ay)或(ax,y)变换时,
这不是相似变换,叫伸缩变换。
x
y
o
B
1.如图表示△AOB和把它缩小后得到的△COD,求它们的相似比
A
C
D
练一练:
x
y
o
2.如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.所得三角形的三个顶点坐标分别是多少?
B
A
C
练一练:
位似变换中对应点的坐标的变化规律:
在平面直角坐标系中,如果位似变换是以原点为位似中心相似比为k,那么位似图形对应点的坐标为ka或-ka,a为原顶点的横纵坐标.
如:在以O为原点的坐标系内,△ABC的顶点坐标分别为A(1,1)、B(2,3)、C(4,2),若以O为位似中心在△ABC同侧放大,相似比为2,则A’坐标为(2,2)、B’(4,6)、C’(8,4);若以O为位似中心在△ABC异侧放大,相似比为2,则A’’(-2,-3)、B’’(-4,-6)、C’’(-8、-4)
在平面直角坐标系中,如果位似变换是以三角形的一个靠近原点的顶点为位似中心,相似比为k,那么位似图形对应点的坐标变成ka-(k-1)或-ka+(k+1),a为原顶点的横纵坐标.
如:在以O为原点的坐标系内,△ABC的顶点坐标分别为A(1,1)、B(2,3)、C(4,2),若以A为位似中心在△ABC同侧放大,相似比为2,则A’坐标为(1,1)、B’(3,5)、C’(7,3);若以O为位似中心在△ABC异侧放大,相似比为2,则A’’(1,1)、B’’(-1,-3)、C’’(-5、-1)。
课堂小结:
1、如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,
那么这样的两个图形叫做 。
2、
这个点叫做 。
3、这时的相似比又称为
。
4、位似图形上任意一对对应点到位似中
心的距离之比等于
。
5.
在以坐标原点为位似中心的位似变换中若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为
(kx,ky)或(―kx,―ky)
6、在平面直角坐标系中在作(x,y)
?
(x,ay)或(ax,y)变换时,
叫伸缩变换。
位似图形
位似中心
位似比
位似比
