青岛版八年级数学上册课件:1.2.2怎样判定三角形全等(共17张PPT)
文档属性
| 名称 | 青岛版八年级数学上册课件:1.2.2怎样判定三角形全等(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 09:58:30 | ||
图片预览






文档简介
(共17张PPT)
第一章
平面图形的全等与相似
§1.2.2怎样判定三角形全等
【教学目标】
知识目标:
1.掌握三角形全等的“ASA和AAS”条件。
2.能初步应用“ASA和AAS”条件判定两个三角形全等.
能力目标:
在探索三角形全等条件及其运用过程中,能够进行有条理的思考并进行简单的推理.
情感目标:
通过探索和实践的过程体会数学思维的乐趣,激发应用数学的意识.
两个三角形,具备哪些条件才全等呢?
实验与探究
做一做:已知:∠
=
700、∠
=
500、a
=
5厘米。在硬纸片上画出△ABC,使∠B
=
∠
、∠C
=
∠
、BC
=
a。
剪下你画出的三角形,与其他同学剪得的三角形进行比较,这些三角形能重合吗?
做一做:改变∠
,∠
的大小(∠
+∠
<
1800
)或改变线段a的长短,按同一条件与同学再做一次,所剪得的三角形还能重合吗?
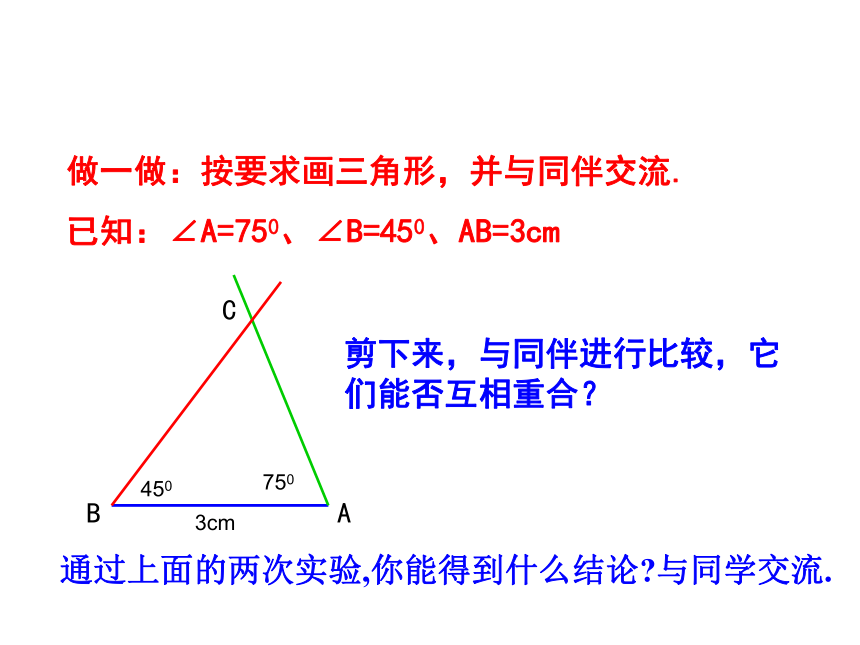
做一做:按要求画三角形,并与同伴交流.
已知:∠A=750、∠B=450、AB=3cm
B
A
C
750
450
3cm
剪下来,与同伴进行比较,它们能否互相重合?
通过上面的两次实验,你能得到什么结论?与同学交流.
两角及其夹边分别相等的两个三角形全等.
简写成“角边角”或“ASA”.
判定方法2:
∵
如何用符号语言来表达呢?
证明:在△ABC与△A
B
C
中
∠A=∠A
∴△ABC≌△A’B’C’(ASA)
A
C
B
A
′
C
B
′
′
′
′
′
′
∠B=∠B
′
′
′
AB=A
B
∵
你能运用数学符号规范的写出这个题目的证明过程吗?
如图,
,
,
全等吗?为什么?
解:
在△ABD和△CDB中
∴
△ABD≌△CDB
(ASA)
∠1=∠2
∠3=∠4
(公共边)
∵
在△ABC和△A'B'C'中,
∠A=∠A',
∠B=∠B',BC=B'C',
△ABC和△A'B'C'全等吗?为什么?
A
C
B
B'
A'
C'
探索
分析:能否转化为ASA?
证明:∵
∠A=∠A',
∠B=∠B'(已知)
∴∠C=∠C'(三角形内角和定理)
∠B=∠B'
在△ABC和△A'B'C'中
BC=B'C'
∠C=∠C'
∴△ABC≌△A'B'C'(ASA)
你能从上题中得到什么结论?
结论:如果一个三角形的两个角及其中一角的对边分别与另一个三角形的两个角及其中一角的对边对应相等,那么这两个三角形全等.
这个判定方法可以简单地用“角角边”
或“
AAS”来表示.
如何用符号语言来表达呢?
证明:在△ABC与△A
B
C
中
∠A=∠A
∴△ABC≌△A’B’C’(AAS)
A
C
B
A
′
C
B
′
′
′
′
′
′
∠B=∠B
′
′
′
BC=B
C
例2、已知:如图,AB为
的角平分线
,∠ABD=∠ABC,求证:AC=AD
分析:要证AC=AD,只需证明△ACB≌△ADB,根据“ASA”即可证。
证明:
在△ACB和△ADB中
∴
△ACB≌△ADB
(ASA)
∴AC=AD
∵
A
C
D
B
∠1=∠2
AB=AB
(公共边)
∠ABC=∠ABD
∵
AB为
的角平分线
∴
∠CAB=∠DAB
1
2
回顾与反思
1、
请同学们想一想:通过本节课学习,你得出了哪些结论?
2、你积累了哪些探索问题的数学思想方法?
小结
(1)
两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2)
两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
知识要点:
解题思路:探索三角形全等的关键是寻找满足全等的三个条件,在应用时应从两方面去找:一是已知中包含的(直接条件或间接条件),二是图形中的隐含条件(如公共边、公共角、对顶角等)
找条件归结成两句话:已知中找,图形中看
数学方法:数形结合、类比法、逆向思维
达标检测
2、如图所示,在△ABC中,已知AB=AC,∠D=∠E
求证:CD=BE,BD=CE
1、如图所示,∠1=∠2,∠ABC=∠ADE,AB=AD
求证:BC=DE
谢谢指导!
第一章
平面图形的全等与相似
§1.2.2怎样判定三角形全等
【教学目标】
知识目标:
1.掌握三角形全等的“ASA和AAS”条件。
2.能初步应用“ASA和AAS”条件判定两个三角形全等.
能力目标:
在探索三角形全等条件及其运用过程中,能够进行有条理的思考并进行简单的推理.
情感目标:
通过探索和实践的过程体会数学思维的乐趣,激发应用数学的意识.
两个三角形,具备哪些条件才全等呢?
实验与探究
做一做:已知:∠
=
700、∠
=
500、a
=
5厘米。在硬纸片上画出△ABC,使∠B
=
∠
、∠C
=
∠
、BC
=
a。
剪下你画出的三角形,与其他同学剪得的三角形进行比较,这些三角形能重合吗?
做一做:改变∠
,∠
的大小(∠
+∠
<
1800
)或改变线段a的长短,按同一条件与同学再做一次,所剪得的三角形还能重合吗?
做一做:按要求画三角形,并与同伴交流.
已知:∠A=750、∠B=450、AB=3cm
B
A
C
750
450
3cm
剪下来,与同伴进行比较,它们能否互相重合?
通过上面的两次实验,你能得到什么结论?与同学交流.
两角及其夹边分别相等的两个三角形全等.
简写成“角边角”或“ASA”.
判定方法2:
∵
如何用符号语言来表达呢?
证明:在△ABC与△A
B
C
中
∠A=∠A
∴△ABC≌△A’B’C’(ASA)
A
C
B
A
′
C
B
′
′
′
′
′
′
∠B=∠B
′
′
′
AB=A
B
∵
你能运用数学符号规范的写出这个题目的证明过程吗?
如图,
,
,
全等吗?为什么?
解:
在△ABD和△CDB中
∴
△ABD≌△CDB
(ASA)
∠1=∠2
∠3=∠4
(公共边)
∵
在△ABC和△A'B'C'中,
∠A=∠A',
∠B=∠B',BC=B'C',
△ABC和△A'B'C'全等吗?为什么?
A
C
B
B'
A'
C'
探索
分析:能否转化为ASA?
证明:∵
∠A=∠A',
∠B=∠B'(已知)
∴∠C=∠C'(三角形内角和定理)
∠B=∠B'
在△ABC和△A'B'C'中
BC=B'C'
∠C=∠C'
∴△ABC≌△A'B'C'(ASA)
你能从上题中得到什么结论?
结论:如果一个三角形的两个角及其中一角的对边分别与另一个三角形的两个角及其中一角的对边对应相等,那么这两个三角形全等.
这个判定方法可以简单地用“角角边”
或“
AAS”来表示.
如何用符号语言来表达呢?
证明:在△ABC与△A
B
C
中
∠A=∠A
∴△ABC≌△A’B’C’(AAS)
A
C
B
A
′
C
B
′
′
′
′
′
′
∠B=∠B
′
′
′
BC=B
C
例2、已知:如图,AB为
的角平分线
,∠ABD=∠ABC,求证:AC=AD
分析:要证AC=AD,只需证明△ACB≌△ADB,根据“ASA”即可证。
证明:
在△ACB和△ADB中
∴
△ACB≌△ADB
(ASA)
∴AC=AD
∵
A
C
D
B
∠1=∠2
AB=AB
(公共边)
∠ABC=∠ABD
∵
AB为
的角平分线
∴
∠CAB=∠DAB
1
2
回顾与反思
1、
请同学们想一想:通过本节课学习,你得出了哪些结论?
2、你积累了哪些探索问题的数学思想方法?
小结
(1)
两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2)
两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
知识要点:
解题思路:探索三角形全等的关键是寻找满足全等的三个条件,在应用时应从两方面去找:一是已知中包含的(直接条件或间接条件),二是图形中的隐含条件(如公共边、公共角、对顶角等)
找条件归结成两句话:已知中找,图形中看
数学方法:数形结合、类比法、逆向思维
达标检测
2、如图所示,在△ABC中,已知AB=AC,∠D=∠E
求证:CD=BE,BD=CE
1、如图所示,∠1=∠2,∠ABC=∠ADE,AB=AD
求证:BC=DE
谢谢指导!
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
