人教版八年级数学上册 14.1.3 积的乘方课件(共26张PPT)
文档属性
| 名称 | 人教版八年级数学上册 14.1.3 积的乘方课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 276.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 09:46:19 | ||
图片预览








文档简介
(共26张PPT)
第十四章
整式的乘法与因式分解
14.1.3
积的乘方
【学习目标】
1.理解并掌握积的乘方的运算性质。
2.探索积的乘方的过程。
【课前预习】
1.下列运算正确的是(
)
A.(-a?)?=a5
B.(-a?)?=a6
C.(-3a?)?=6a4
D.(-3a?)?=9a5
2.计算
的结果是(
)
3.计算
(2÷3)2006×(1.5)2005×(-1)2009
A.-2÷3
B.-3÷2
C.2÷3
D.3÷2
4.(-3x?y?)?的值是(
)
A.-6x4y5
B.-9x4y9
C.9x6y4
D.6x6y4
5.下列计算正确的是(
)
A.x4?x4=x16
D.a+2a=3a
【课前预习】答案
1.B
2.B
3.A
4.C
5.D
回顾
思考
幂的意义:
a·a·
…
·a
n个a
an
=
同底数幂的乘法运算法则:
am
·
an
=
am+n
(m,n都是正整数)
幂的乘方运算法则:
(am)n=
(m、n都是正整数)
amn
【学习探究】
知识回顾
填空:
1.
am+am=_____,依据________________.
2.
a3·a5=____,依据_______________
________.
3.
若am=8,an=30,则am+n=____.
4.
(a4)3=_____,依据___________________.
5.
(m4)2+m5·m3=____,(a3)5·(a2)2=____.
2am
合并同类项法则
a8
同底数幂乘法的
运算性质
240
a12
幂的乘方的运算性质
2m8
a19
⑴
(1×2)4=____;
14×24
=_____;
⑵
[3×(-2)]3=_____;
33×(-2)3=________;
⑶
(
)2
=
16
16
-216
-216
你发现了什么?
填空:
(ab)n=_____.
(n为正整数)
anbn
=
3、观察、猜想:
(ab)3与a3b3
是什么关系呢?
(ab)3=
说出以上推导过程中每一步变形的依据。
(ab)·(ab)·(ab)=
(aaa)
·(bbb)=
a3b3
乘方的意义
乘方的意义
乘法交换律、结合律
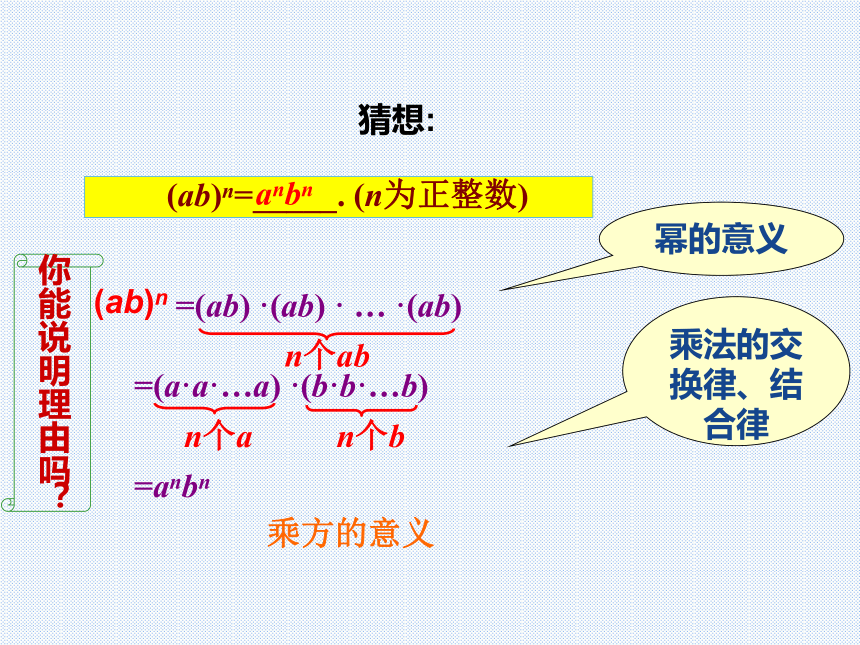
(ab)n=_____.(n为正整数)
猜想:
你能说明理由吗?
=(ab)
·(ab)
·
…
·(ab)
n个ab
=(a·a·…a)
·(b·b·…b)
n个a
n个b
=anbn
(ab)n
幂的意义
乘法的交换律、结合律
乘方的意义
(ab)n=_____.
(n为正整数)
anbn
积的乘方的运算性质:
结论:
(ab)n=_____.
(n为正整数)
anbn
你能用文字语言叙述这个性质吗?
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____.
(n为正整数)
anbn
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
例1
计算:
(5m)3
(-xy2)3
(3)(3×103)2
125m3
-x3
y6
9×106
1.计算:
(-ab)5
(2)
(x2y3)4
(3)
(4×103)2
(4)
(-3a3)3
×
×
x3
4
2.下面的计算是否正确?如果有错误,请改正.
(xy2)3=
x
y6
(
)
(-2b2)2=-4
b4
(
)
-a5
b5
x8y12
16
×106
-27a9
练习
积的乘方的运算性质:
(ab)n=_____.
(n为正整数)
anbn
(abc)n
=
anbncn
(n为正整数)
请你推广:
(abc)n
=[(ab)c]n
=anbncn
=(ab)ncn
积的乘方的运算性质:
(ab)n=_____.
(n为正整数)
anbn
(abc)n
=
anbncn
(n为正整数)
例2
计算:
(3xy2)2
(-2ab3c2)4
9x2y4
16
a4
b12c8
(
)
(
)
(
)
(
)
(
)
1.在括号里填写适当的计算依据:
(1)[(3x)2]3
=(3x)6
=36x6
=729x6
(2)[(3x)2]3
=(9x2)3
=93(x2)3
=729x6
积的乘方的运算性质
积的乘方的运算性质
积的乘方的运算性质
幂的乘方的运算性质
幂的乘方的运算性质
练习
2.计算:
(1)
(-3x2y)3
(2)
(-5ab)2
(3)
(2xnym)2
(4)
(-2xy2z3)4
(1)-27x6y3
(2)25a2b2
(3)4x2ny2m
(4)16x4y8z12
3.计算:
⑴
(-a2)3.(-a3)2
⑵
-(n2).(-n5)3
⑶
a5.a3+(2a2)4
⑷
(-2a)3-(-a).(a)2
-a12
n17
-a12
-7a3
=1
6个
6个2
解:原式
解:原式
你会计算吗?
试一试
你会计算吗?
逆用积的乘方的运算性质
积的乘方的运算性质:
(ab)n=_____.
(n为正整数)
anbn
计算:
1
4
3
4
小结
{
幂的意义:
a·a·
…
·a
n个a
an
=
同底数幂的乘法运算法则:
am
·
an=am+n
幂的乘方运算法则:
(ab)n=anbn
积的乘方=
每个因式分别乘方后的积
反向使用
am
·
an
=am+n
(am)n
=amn
an·bn
=
(ab)n
可使某些计算简捷。
小结
2.
【课后练习】
1.若
,则m、n的值分别为(
)
A.9,5
B.3,5
C.5,3
D.6,12
2.计算
的结果为(
)
A.
B.
C.
D.-2016
3.下列计算结果不正确的是( )
A.ab(ab)?=a3b3
B.(﹣p3)2=p6
C.(﹣2ab2)3=﹣8a3b6
D.(﹣3pq)2=﹣9p2q2
4.下列运算中,计算结果正确的是( )
A.a2?a3=a6
B.(a2)3=a5
C.(a2b)2=a2b2
D.(π﹣1)0=1
5.2101×0.5100的计算结果正确的是( )
A.1
B.2
C.0.5
D.10
6.已知2a=3,2b=6,2c=12,那么a,b,c间的大小关系是( ).
A.a+b>c
B.2b<a+c
C.2b=a+c
D.2a<b+c
7.下列四个式子:①(-3x3)3=-9x3;②(-5ab)2=-25a2b2;③(xy2)2=x2y4;④(-2ab3c2)4=16a4b12c8.其中正确的有( ).
A.0个
B.1个
C.2个
D.3个
8.下列计算正确的是(
)
9.下列的运算中,其结果正确的是( )
10.计算的结果是(
)
11.计算:
________.
12.在横线上填写适当的整式:16a16=(___)2.
13.计算0.125100×8101=____.
14.已知x?-y?=1,则
_____.
15.计算:(-a?)?+(-a?)?=________.
【课后练习】答案
1.B
2.A
3.D
4.D
5.B
6.C
7.C
8.D
9.B
10.D
11.
12.4a8.
13.8
14.1
15.0
第十四章
整式的乘法与因式分解
14.1.3
积的乘方
【学习目标】
1.理解并掌握积的乘方的运算性质。
2.探索积的乘方的过程。
【课前预习】
1.下列运算正确的是(
)
A.(-a?)?=a5
B.(-a?)?=a6
C.(-3a?)?=6a4
D.(-3a?)?=9a5
2.计算
的结果是(
)
3.计算
(2÷3)2006×(1.5)2005×(-1)2009
A.-2÷3
B.-3÷2
C.2÷3
D.3÷2
4.(-3x?y?)?的值是(
)
A.-6x4y5
B.-9x4y9
C.9x6y4
D.6x6y4
5.下列计算正确的是(
)
A.x4?x4=x16
D.a+2a=3a
【课前预习】答案
1.B
2.B
3.A
4.C
5.D
回顾
思考
幂的意义:
a·a·
…
·a
n个a
an
=
同底数幂的乘法运算法则:
am
·
an
=
am+n
(m,n都是正整数)
幂的乘方运算法则:
(am)n=
(m、n都是正整数)
amn
【学习探究】
知识回顾
填空:
1.
am+am=_____,依据________________.
2.
a3·a5=____,依据_______________
________.
3.
若am=8,an=30,则am+n=____.
4.
(a4)3=_____,依据___________________.
5.
(m4)2+m5·m3=____,(a3)5·(a2)2=____.
2am
合并同类项法则
a8
同底数幂乘法的
运算性质
240
a12
幂的乘方的运算性质
2m8
a19
⑴
(1×2)4=____;
14×24
=_____;
⑵
[3×(-2)]3=_____;
33×(-2)3=________;
⑶
(
)2
=
16
16
-216
-216
你发现了什么?
填空:
(ab)n=_____.
(n为正整数)
anbn
=
3、观察、猜想:
(ab)3与a3b3
是什么关系呢?
(ab)3=
说出以上推导过程中每一步变形的依据。
(ab)·(ab)·(ab)=
(aaa)
·(bbb)=
a3b3
乘方的意义
乘方的意义
乘法交换律、结合律
(ab)n=_____.(n为正整数)
猜想:
你能说明理由吗?
=(ab)
·(ab)
·
…
·(ab)
n个ab
=(a·a·…a)
·(b·b·…b)
n个a
n个b
=anbn
(ab)n
幂的意义
乘法的交换律、结合律
乘方的意义
(ab)n=_____.
(n为正整数)
anbn
积的乘方的运算性质:
结论:
(ab)n=_____.
(n为正整数)
anbn
你能用文字语言叙述这个性质吗?
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____.
(n为正整数)
anbn
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
例1
计算:
(5m)3
(-xy2)3
(3)(3×103)2
125m3
-x3
y6
9×106
1.计算:
(-ab)5
(2)
(x2y3)4
(3)
(4×103)2
(4)
(-3a3)3
×
×
x3
4
2.下面的计算是否正确?如果有错误,请改正.
(xy2)3=
x
y6
(
)
(-2b2)2=-4
b4
(
)
-a5
b5
x8y12
16
×106
-27a9
练习
积的乘方的运算性质:
(ab)n=_____.
(n为正整数)
anbn
(abc)n
=
anbncn
(n为正整数)
请你推广:
(abc)n
=[(ab)c]n
=anbncn
=(ab)ncn
积的乘方的运算性质:
(ab)n=_____.
(n为正整数)
anbn
(abc)n
=
anbncn
(n为正整数)
例2
计算:
(3xy2)2
(-2ab3c2)4
9x2y4
16
a4
b12c8
(
)
(
)
(
)
(
)
(
)
1.在括号里填写适当的计算依据:
(1)[(3x)2]3
=(3x)6
=36x6
=729x6
(2)[(3x)2]3
=(9x2)3
=93(x2)3
=729x6
积的乘方的运算性质
积的乘方的运算性质
积的乘方的运算性质
幂的乘方的运算性质
幂的乘方的运算性质
练习
2.计算:
(1)
(-3x2y)3
(2)
(-5ab)2
(3)
(2xnym)2
(4)
(-2xy2z3)4
(1)-27x6y3
(2)25a2b2
(3)4x2ny2m
(4)16x4y8z12
3.计算:
⑴
(-a2)3.(-a3)2
⑵
-(n2).(-n5)3
⑶
a5.a3+(2a2)4
⑷
(-2a)3-(-a).(a)2
-a12
n17
-a12
-7a3
=1
6个
6个2
解:原式
解:原式
你会计算吗?
试一试
你会计算吗?
逆用积的乘方的运算性质
积的乘方的运算性质:
(ab)n=_____.
(n为正整数)
anbn
计算:
1
4
3
4
小结
{
幂的意义:
a·a·
…
·a
n个a
an
=
同底数幂的乘法运算法则:
am
·
an=am+n
幂的乘方运算法则:
(ab)n=anbn
积的乘方=
每个因式分别乘方后的积
反向使用
am
·
an
=am+n
(am)n
=amn
an·bn
=
(ab)n
可使某些计算简捷。
小结
2.
【课后练习】
1.若
,则m、n的值分别为(
)
A.9,5
B.3,5
C.5,3
D.6,12
2.计算
的结果为(
)
A.
B.
C.
D.-2016
3.下列计算结果不正确的是( )
A.ab(ab)?=a3b3
B.(﹣p3)2=p6
C.(﹣2ab2)3=﹣8a3b6
D.(﹣3pq)2=﹣9p2q2
4.下列运算中,计算结果正确的是( )
A.a2?a3=a6
B.(a2)3=a5
C.(a2b)2=a2b2
D.(π﹣1)0=1
5.2101×0.5100的计算结果正确的是( )
A.1
B.2
C.0.5
D.10
6.已知2a=3,2b=6,2c=12,那么a,b,c间的大小关系是( ).
A.a+b>c
B.2b<a+c
C.2b=a+c
D.2a<b+c
7.下列四个式子:①(-3x3)3=-9x3;②(-5ab)2=-25a2b2;③(xy2)2=x2y4;④(-2ab3c2)4=16a4b12c8.其中正确的有( ).
A.0个
B.1个
C.2个
D.3个
8.下列计算正确的是(
)
9.下列的运算中,其结果正确的是( )
10.计算的结果是(
)
11.计算:
________.
12.在横线上填写适当的整式:16a16=(___)2.
13.计算0.125100×8101=____.
14.已知x?-y?=1,则
_____.
15.计算:(-a?)?+(-a?)?=________.
【课后练习】答案
1.B
2.A
3.D
4.D
5.B
6.C
7.C
8.D
9.B
10.D
11.
12.4a8.
13.8
14.1
15.0
