人教版九年级上册 数学 课件: 24.2.1点和圆的位置关系(共24张PPT)
文档属性
| 名称 | 人教版九年级上册 数学 课件: 24.2.1点和圆的位置关系(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 09:41:27 | ||
图片预览




文档简介
(共24张PPT)
24.2与圆有关的位置关系
24.2.1点和圆的位置关系
我国射击运动员在奥运会上屡获金牌,为我国赢得荣誉,右图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不等的圆)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
观
察
r
问题2:设⊙O半径为
r
,
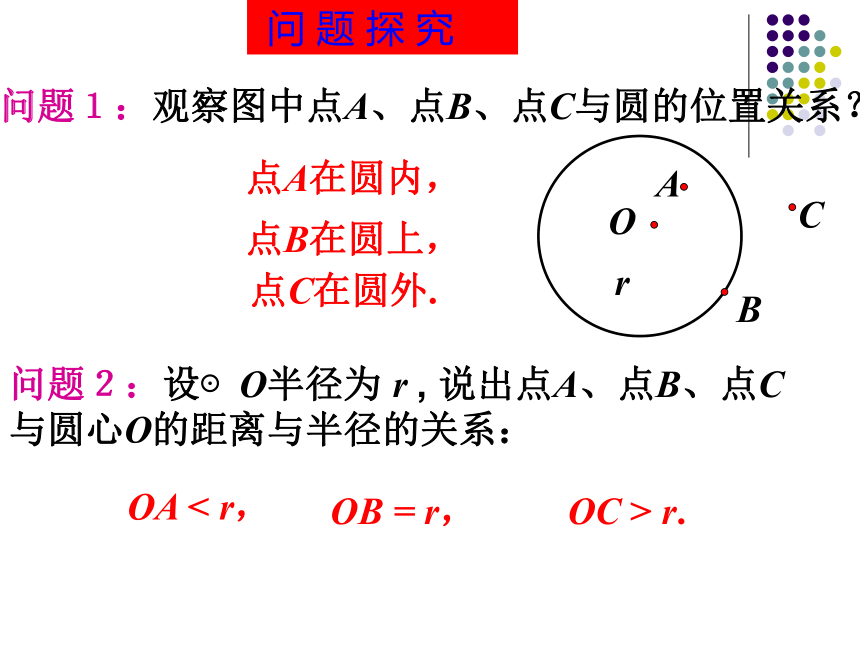
说出点A、点B、点C与圆心O的距离与半径的关系:
C
O
A
B
OC
>
r.
问题1:观察图中点A、点B、点C与圆的位置关系?
点C在圆外.
点A在圆内,
点B在圆上,
OA
<
r,
OB
=
r,
问
题
探
究
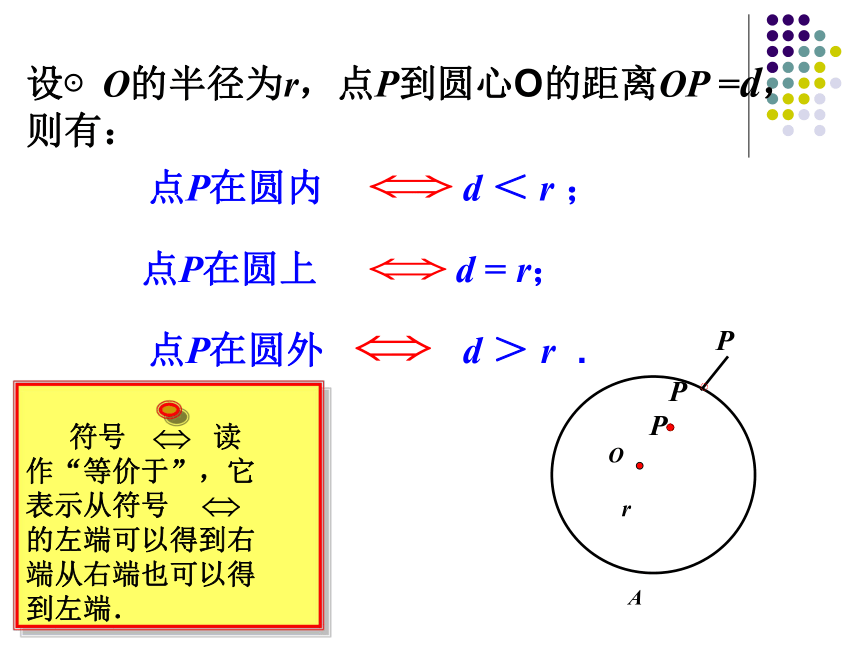
设⊙O的半径为r,点P到圆心O的距离OP
=d,则有:
点P在圆上
d
=
r;
点P在圆外
d
>
r
.
点P在圆内
d
<
r
;
符号
读
作“等价于”,它
表示从符号
的左端可以得到右
端从右端也可以得
到左端.
r
O
A
P
P
P
练一练
1、⊙O的半径10cm,A、B、C三点到圆心O的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
。
圆内
圆上
圆外
2、已知AB为⊙O的直径,P为⊙O
上任意一点,则点P关于AB的对称点P′与⊙
O的位置为(
)
(A)在⊙O内
(B)在⊙O
外
(C)在⊙O
上
(D)不能确定
c
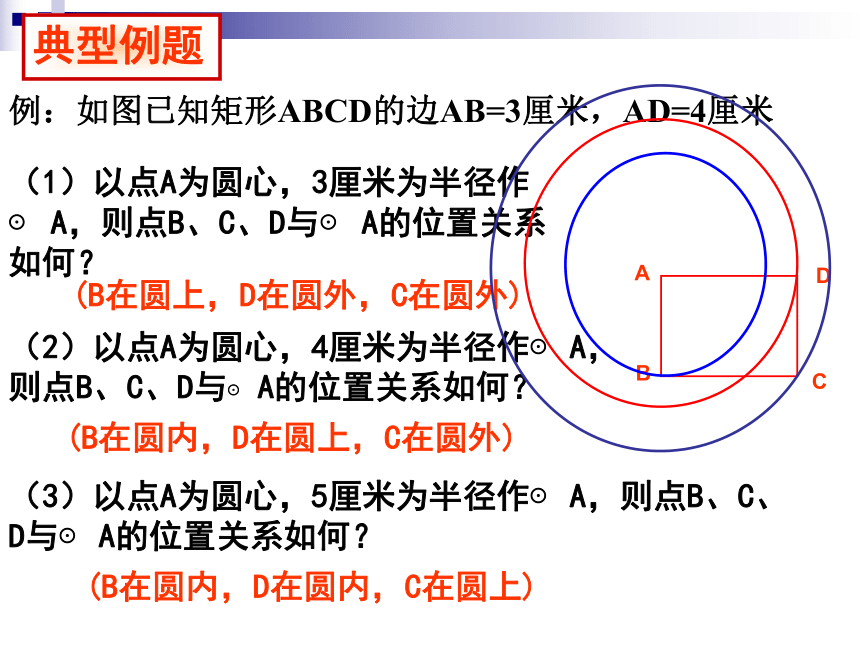
例:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
典型例题
A
D
C
B
(1)以点A为圆心,3厘米为半径作⊙
A,则点B、C、D与⊙
A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作⊙
A,则点B、C、D与⊙
A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作⊙
A,则点B、C、D与⊙
A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
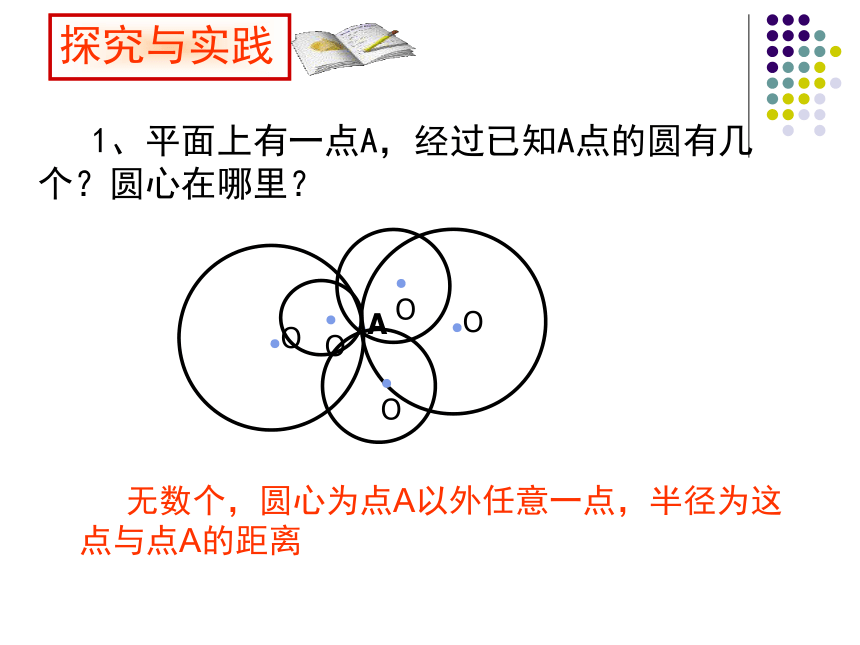
1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
探究与实践
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离
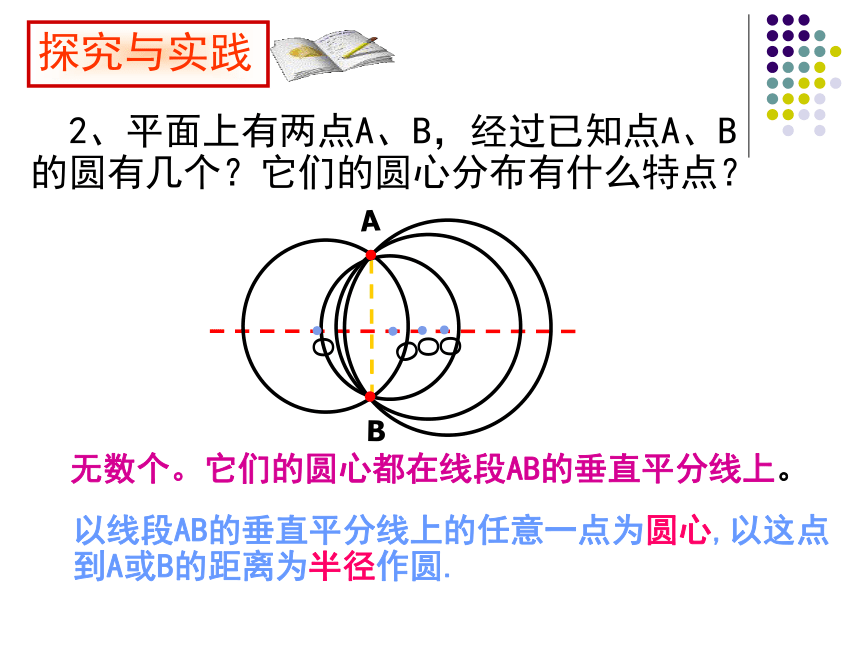
2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点?
探究与实践
●O
●
O
●O
●O
A
B
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
无数个。它们的圆心都在线段AB的垂直平分线上。
(1)经过不在同一条直线上的三点作一个圆,如何确定这个圆的圆心?
?
思
考
经过已知的三点作圆,这样的圆能作出多少个?
3、如图,平面上有不在同一直线上三点A、B、C,经过A、B、C三点的圆有几个?圆心在哪里?
归纳结论:
不在同一条直线上的三个点确定一个圆。
探究与实践
┓
●B
●C
经过B、C两点的圆的圆心在线段BC的垂直平分线上.
┏
●A
经过A、B、C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
●O
经过A、B两点的圆的圆心在线段AB的垂直平分线上.
经过三角形三个顶点可以画一个圆,并且只能画一个.
一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
经过三角形三个顶点的圆叫做三角形的外接圆。
三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。
这个三角形叫做这个圆的内接三角形。
三角形外接圆的圆心叫做这个三角形的外心。
想一想
●O
A
B
C
有关概念
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
做一做
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
练一练
1、判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆(
).
(2)任意一个圆有且只有一个内接三角形(
)
(3)经过三点一定可以确定一个圆(
)
(4)三角形的外心到三角形各顶点的距离相等(
)
2、若一个三角形的外心在一边上,则此三角形的
形状为(
)
A、锐角三角形
B、直角三角形
C、钝角三角形
D、等腰三角形
√
×
×
√
B
如图,已知等边三角形ABC中,边长为
6cm,求它的外接圆半径。
典型例题
O
E
D
C
B
A
如图,等腰⊿ABC中,
,
,求⊿ABC外接圆的半径。
练习
O
A
D
C
B
思考
1
小结与归纳
◆用数量关系判断点和圆的位置关系。
◆不在同一直线上的三点确定一个圆。
◆求解直角三角形、等边三角形、等腰三角
形等特殊三角形的外接圆半径。
◆在求解等腰三角形外接圆半径时,运用了
方程的思想。
(2)经过同一条直线三个点能作出一个圆吗?
?
思
考
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l,这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
什么叫反证法?
求证:在一个三角形中,至少有一个内角小于或等于60度。(用反证法)
练一练
反证法常用于解决用直接证法不易证明或不能证明的命题,主要有:
(1)命题的结论是否定型的;
(2)命题的结论是无限型的;
(3)命题的结论是“至多”或“至少”型的.
爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的的安全区域,已知这个导火索的长度18cm,如果点导火索的人以每秒6.5m的速度撤离,那么是否安全?为什么?
生活问题数学化
驶向胜利的彼岸
小结
通过这一节的学习:
我最大的收获是______________
我对自己的表现评价如何_____________
我从同学身上学到了________________
心有多大,舞台就有多大;
放飞你的梦想,乐于去探索吧!
下课啦!
再
见
24.2与圆有关的位置关系
24.2.1点和圆的位置关系
我国射击运动员在奥运会上屡获金牌,为我国赢得荣誉,右图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不等的圆)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
观
察
r
问题2:设⊙O半径为
r
,
说出点A、点B、点C与圆心O的距离与半径的关系:
C
O
A
B
OC
>
r.
问题1:观察图中点A、点B、点C与圆的位置关系?
点C在圆外.
点A在圆内,
点B在圆上,
OA
<
r,
OB
=
r,
问
题
探
究
设⊙O的半径为r,点P到圆心O的距离OP
=d,则有:
点P在圆上
d
=
r;
点P在圆外
d
>
r
.
点P在圆内
d
<
r
;
符号
读
作“等价于”,它
表示从符号
的左端可以得到右
端从右端也可以得
到左端.
r
O
A
P
P
P
练一练
1、⊙O的半径10cm,A、B、C三点到圆心O的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
。
圆内
圆上
圆外
2、已知AB为⊙O的直径,P为⊙O
上任意一点,则点P关于AB的对称点P′与⊙
O的位置为(
)
(A)在⊙O内
(B)在⊙O
外
(C)在⊙O
上
(D)不能确定
c
例:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
典型例题
A
D
C
B
(1)以点A为圆心,3厘米为半径作⊙
A,则点B、C、D与⊙
A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作⊙
A,则点B、C、D与⊙
A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作⊙
A,则点B、C、D与⊙
A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
探究与实践
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离
2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点?
探究与实践
●O
●
O
●O
●O
A
B
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
无数个。它们的圆心都在线段AB的垂直平分线上。
(1)经过不在同一条直线上的三点作一个圆,如何确定这个圆的圆心?
?
思
考
经过已知的三点作圆,这样的圆能作出多少个?
3、如图,平面上有不在同一直线上三点A、B、C,经过A、B、C三点的圆有几个?圆心在哪里?
归纳结论:
不在同一条直线上的三个点确定一个圆。
探究与实践
┓
●B
●C
经过B、C两点的圆的圆心在线段BC的垂直平分线上.
┏
●A
经过A、B、C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
●O
经过A、B两点的圆的圆心在线段AB的垂直平分线上.
经过三角形三个顶点可以画一个圆,并且只能画一个.
一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
经过三角形三个顶点的圆叫做三角形的外接圆。
三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。
这个三角形叫做这个圆的内接三角形。
三角形外接圆的圆心叫做这个三角形的外心。
想一想
●O
A
B
C
有关概念
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
做一做
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
练一练
1、判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆(
).
(2)任意一个圆有且只有一个内接三角形(
)
(3)经过三点一定可以确定一个圆(
)
(4)三角形的外心到三角形各顶点的距离相等(
)
2、若一个三角形的外心在一边上,则此三角形的
形状为(
)
A、锐角三角形
B、直角三角形
C、钝角三角形
D、等腰三角形
√
×
×
√
B
如图,已知等边三角形ABC中,边长为
6cm,求它的外接圆半径。
典型例题
O
E
D
C
B
A
如图,等腰⊿ABC中,
,
,求⊿ABC外接圆的半径。
练习
O
A
D
C
B
思考
1
小结与归纳
◆用数量关系判断点和圆的位置关系。
◆不在同一直线上的三点确定一个圆。
◆求解直角三角形、等边三角形、等腰三角
形等特殊三角形的外接圆半径。
◆在求解等腰三角形外接圆半径时,运用了
方程的思想。
(2)经过同一条直线三个点能作出一个圆吗?
?
思
考
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l,这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
什么叫反证法?
求证:在一个三角形中,至少有一个内角小于或等于60度。(用反证法)
练一练
反证法常用于解决用直接证法不易证明或不能证明的命题,主要有:
(1)命题的结论是否定型的;
(2)命题的结论是无限型的;
(3)命题的结论是“至多”或“至少”型的.
爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的的安全区域,已知这个导火索的长度18cm,如果点导火索的人以每秒6.5m的速度撤离,那么是否安全?为什么?
生活问题数学化
驶向胜利的彼岸
小结
通过这一节的学习:
我最大的收获是______________
我对自己的表现评价如何_____________
我从同学身上学到了________________
心有多大,舞台就有多大;
放飞你的梦想,乐于去探索吧!
下课啦!
再
见
同课章节目录
