人教版九年级上册 数学 24.2.2 直线与圆的位置关系课件(共24张PPT)
文档属性
| 名称 | 人教版九年级上册 数学 24.2.2 直线与圆的位置关系课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 08:55:52 | ||
图片预览



文档简介
(共24张PPT)
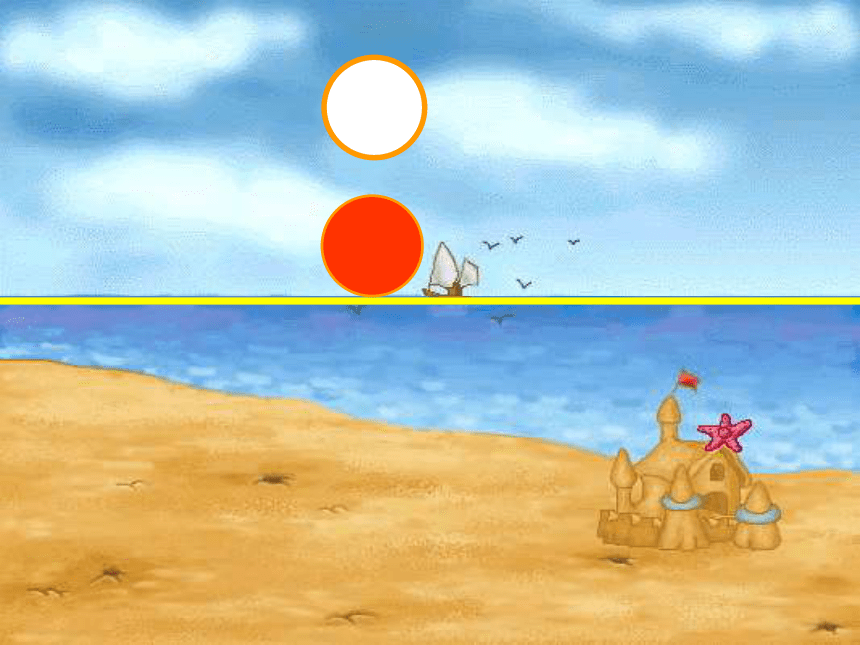
点和圆的位置关系有哪几种?
A
B
C
d
O
点到圆心距离为d
⊙O半径为r
回
顾:
点在圆外
点在圆上
点在圆内
d>r;
d=r;
d位置关系
数量关系
a
.A
D
相关知识点回忆
直线外一点到这条直线的垂线段的长度叫点到直线的距离。
●O
●O
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数
a(地平线)
a(地平线)
●O
●O
●O
三
你发现这个自然现象反映出直线和圆的公共点个数有
种情况
海上日出
观察探究一
●
●
●
●
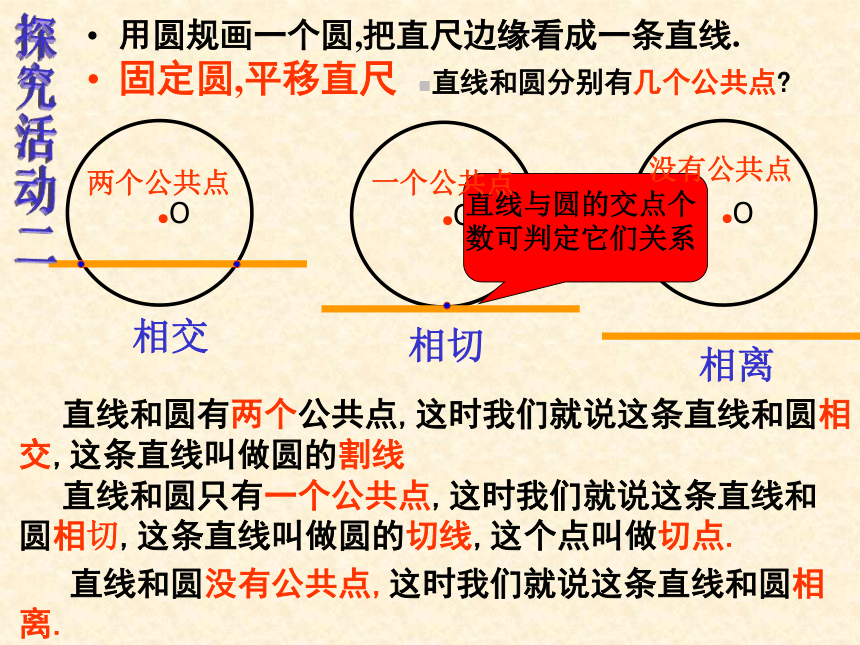
用圆规画一个圆,把直尺边缘看成一条直线.
固定圆,平移直尺
直线和圆分别有几个公共点?
●O
●O
相交
●O
相切
相离
直线与圆的交点个数可判定它们关系
探究活动二
直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线
直线和圆没有公共点,这时我们就说这条直线和圆相离.
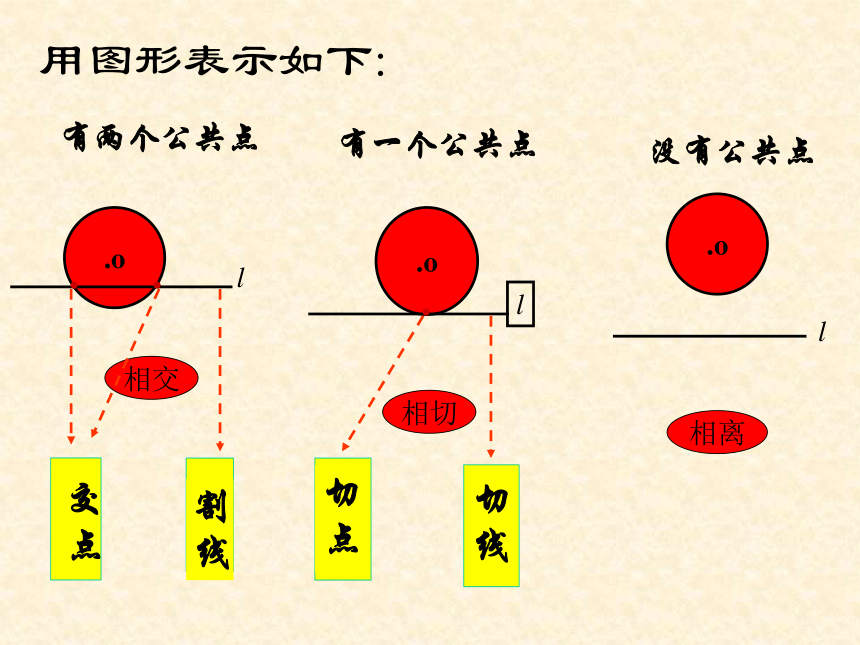
两个公共点
没有公共点
一个公共点
用图形表示如下:
.o
.o
l
l
相切
相交
切线
切点
割线
.
.
.
没有公共点
有一个公共点
有两个公共点
.o
l
相离
交点
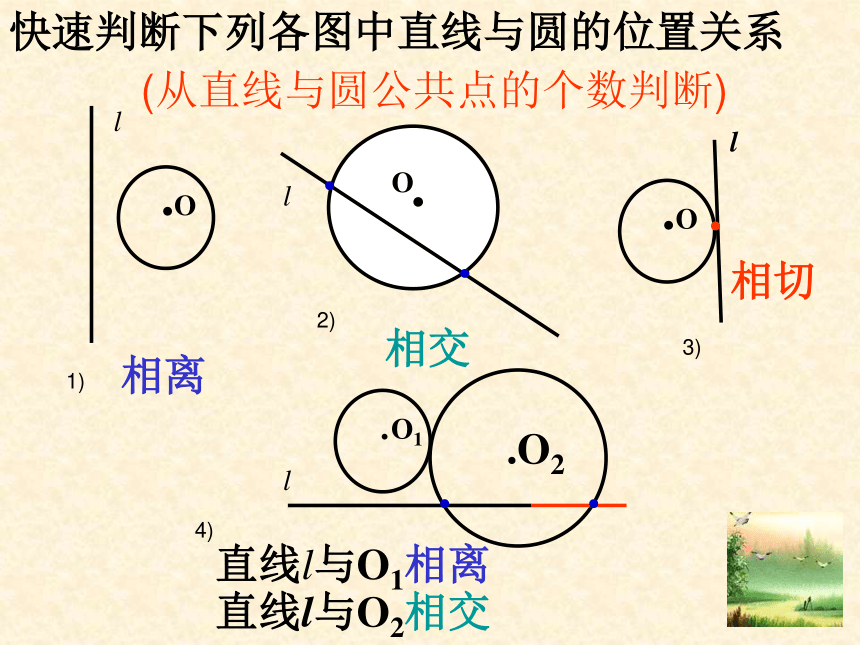
快速判断下列各图中直线与圆的位置关系
.O
l
.O1
.O
l
.O2
l
l
.
1)
2)
3)
4)
相交
相切
相离
直线l与O1相离
直线l与O2相交
O
(从直线与圆公共点的个数判断)
●
●
●
●
●
?
(1)从图形上不容易判断公共点的个数,该怎么办?
·O
(2)“直线和圆的位置关系”能否可以象
“点和圆的位置关系”一样进行数量分析?
·A
·B
知识内化
揭示结论
动画演示
探讨问题
从数量上探索直线与圆的位置关系
学生活动
d
d
d
.O
.O
.O
r
r
r
d>r
d=r
d.A
.B
C
.D
.E
.F
N
H
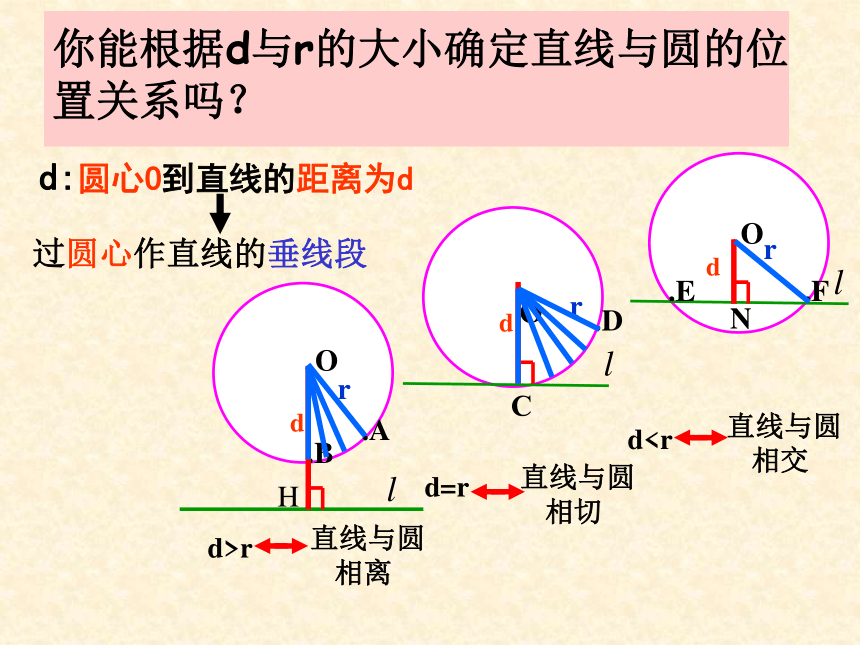
你能根据d与r的大小确定直线与圆的位置关系吗?
直线与圆
相离
直线与圆
相切
直线与圆
相交
d:圆心O到直线的距离为d
过圆心作直线的垂线段
O
O
O
?
?
?
M
M
M
揭示结论
动画演示
探讨问题
直线和圆的位置关系可以转化为
直线和点(圆心)的关系
知识内化
直线
和⊙O
相离
d>r
直线
和⊙O
相交
d直线
和⊙O
相切
d=r
教师活动
点在圆外
d>r
点在圆内
d点在圆上
d=r
转到复习页
如图,圆心O到直线的距离d与⊙O的半径r的大小有什么关系?
●O
●O
相交
●O
相切
相离
直线与圆的位置关系量化
r
r
r
┐d
d
┐
d
┐
1)直线和圆相交
d
r;
d
r;
2)直线和圆相切
3)直线和圆相离
d
r;
<
=
>
d:圆心O到直线的距离为d
过圆心作直线的垂线段
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由
_______________
的个数来判断;
(2)由_________________
的大小关系来判断。
两
直线与圆的公共点
圆心到直线的距离d与半径r
归纳:
1、直线和圆有2个交点,则直线和圆_________;
直线和圆有1个交点,则直线和圆_________;
直线和圆有没有交点,则直线和圆_________;
相交
相切
相离
随堂练习
2、⊙O的半径为3,圆心O到直线l的距离为d,若直线l与⊙O没有公共点,则d为( ):
A.d
>3
B.d<3
C.d
≤3
D.d
=3
3、圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置关系是( ):
A.相离
B.相交
C.相切
D.相切或相交
A
C
3)若AB和⊙O相交,则
.
4、已知⊙O的半径为5,
圆心O到直线AB的距离为d,
根据条件填写d的范围:
1)若AB和⊙O相离,
则
;
2)若AB和⊙O相切,
则
;
d
>
5
d
=
5
d
<
5
0≤
5、已知⊙O的半径为r,
圆心O到直线AB的距离为3,
根据条件填写r的范围:
1)若AB和⊙O相切,
则
;
2)若AB和⊙O相交,
则
;
3)若AB和⊙O相离,
则
;
r
=3
r>
3
0<
r
<
3
2:圆的直径是13
,如果直线与圆心的距离分别是,
(1)
4.5;
(2)
6.5;
(3)
8.
那么直线和圆分别是什么位置关系?有几个公共点?
课本96页
随堂练习
(3)
当
d
=
8时,
有
d
>
r,因此圆与直线相离,没有公共点
当
r
=
6.5时,
有
d
=
r,因此圆与直线相切,
有一个公共点
当
d
=
4.5时,
有
d
<
r,
因此圆与直线相交,
有两个公共点
解:
r=6.5,设直线与圆心的距离为d
如图:∠AOB
=
30°M是OB上的一点,且OM
=5以M为圆心,以r
为半径的圆与
直线OA
有怎样的关系?为什么?
(1)r
=
2
;
(2)
r
=
4
;
(3)
r
=
2.5
.
C
O
B
A
M
5
30°
解:
过
M
作
MC⊥OA
于
C,在
Rt
△OMC
中,
∠AOB
=
30°
MC=
OM=
x5=2.5
1
2
1
2
即圆心
M
到OA的距离
d
=
2.5
.
因此⊙M
和
直线OA
相离.
(3)
当
r
=
2.5时,
因此⊙M
和直线
OA
相切.
(1)
当
r
=
2
时,
(2)
当
r
=
4
时,
因此⊙M
和直线O
A
相交.
2.5
有
d
>
r,
有
d
<
r,
有
d
=
r
,
典型例题
如图:M是OB上的一点,且OM
=5
以M为圆心,半径r=2.5作⊙M.
试问过O的射线
OA与OB所夹的锐角a取什么值时射线OA与
⊙M
(1)相离
(2)相切
(3)相交
?
C
O
B
A
M
5
a
2.5
例题的变式题
解:
过
M
作
MC⊥OA
于
C
1)当∠a
=
30°时,d=r=2.5
此时射线OA与⊙M相切
2)当
30°<
∠a
时
射线OA与⊙M相离
3)当
0
<
∠a
<30°时
射线OA与⊙M相交
<
90°
0
d>r
1
d=r
切点
切线
2
d.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
课堂小结
交点
割线
设⊙O的圆心O到直线的距离为d,半径为r,d.r是
方程(m+9)x2-
(m+6)
x
+1=0的两根,且直线与⊙O相切
时,求m的值?
方程
几何综合练习题
d=r
析:直线与⊙O相切
b2-4ac=0
[-(m+6)]2-4(m+9)=0
解得
m1=
-8
m2=
0
当m=-8时原方程
为x2+
2x+1=0
x1=x2=
-1
当m=0时原方程
为9x2-
6x+1=0
b2-4ac=
[-(m+6)]2-4(m+9)=0
解:由题意可得
x1=x2=
1
3
∴
m=0
(不符合题意舍去)
已知⊙O的半径r=7cm,直线l1
//
l2,且l1与⊙O相切,圆心O到l2的距离为9cm.求l1与l2的距离m.
o
。
l1
l2
A
B
C
l2
能力拓展
A.(-3,-4)
O
x
y
拓展:已知⊙A的直径为6,点A的坐标为(-3,-4),则x轴与⊙A的位置关系是_____,
y轴与⊙A的位置关系是_____。
B
C
4
3
相离
相切
-1
-1
.(-3,-4)
O
x
y
B
C
4
3
-1
-1
思考:若⊙A要与x轴相切,则⊙A该向上移动多少个单位?若⊙A要与x轴相交呢?
知识像一艘船
让它载着我们
驶向理想的
……
点和圆的位置关系有哪几种?
A
B
C
d
O
点到圆心距离为d
⊙O半径为r
回
顾:
点在圆外
点在圆上
点在圆内
d>r;
d=r;
d
数量关系
a
.A
D
相关知识点回忆
直线外一点到这条直线的垂线段的长度叫点到直线的距离。
●O
●O
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数
a(地平线)
a(地平线)
●O
●O
●O
三
你发现这个自然现象反映出直线和圆的公共点个数有
种情况
海上日出
观察探究一
●
●
●
●
用圆规画一个圆,把直尺边缘看成一条直线.
固定圆,平移直尺
直线和圆分别有几个公共点?
●O
●O
相交
●O
相切
相离
直线与圆的交点个数可判定它们关系
探究活动二
直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线
直线和圆没有公共点,这时我们就说这条直线和圆相离.
两个公共点
没有公共点
一个公共点
用图形表示如下:
.o
.o
l
l
相切
相交
切线
切点
割线
.
.
.
没有公共点
有一个公共点
有两个公共点
.o
l
相离
交点
快速判断下列各图中直线与圆的位置关系
.O
l
.O1
.O
l
.O2
l
l
.
1)
2)
3)
4)
相交
相切
相离
直线l与O1相离
直线l与O2相交
O
(从直线与圆公共点的个数判断)
●
●
●
●
●
?
(1)从图形上不容易判断公共点的个数,该怎么办?
·O
(2)“直线和圆的位置关系”能否可以象
“点和圆的位置关系”一样进行数量分析?
·A
·B
知识内化
揭示结论
动画演示
探讨问题
从数量上探索直线与圆的位置关系
学生活动
d
d
d
.O
.O
.O
r
r
r
d>r
d=r
d
.B
C
.D
.E
.F
N
H
你能根据d与r的大小确定直线与圆的位置关系吗?
直线与圆
相离
直线与圆
相切
直线与圆
相交
d:圆心O到直线的距离为d
过圆心作直线的垂线段
O
O
O
?
?
?
M
M
M
揭示结论
动画演示
探讨问题
直线和圆的位置关系可以转化为
直线和点(圆心)的关系
知识内化
直线
和⊙O
相离
d>r
直线
和⊙O
相交
d
和⊙O
相切
d=r
教师活动
点在圆外
d>r
点在圆内
d
d=r
转到复习页
如图,圆心O到直线的距离d与⊙O的半径r的大小有什么关系?
●O
●O
相交
●O
相切
相离
直线与圆的位置关系量化
r
r
r
┐d
d
┐
d
┐
1)直线和圆相交
d
r;
d
r;
2)直线和圆相切
3)直线和圆相离
d
r;
<
=
>
d:圆心O到直线的距离为d
过圆心作直线的垂线段
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由
_______________
的个数来判断;
(2)由_________________
的大小关系来判断。
两
直线与圆的公共点
圆心到直线的距离d与半径r
归纳:
1、直线和圆有2个交点,则直线和圆_________;
直线和圆有1个交点,则直线和圆_________;
直线和圆有没有交点,则直线和圆_________;
相交
相切
相离
随堂练习
2、⊙O的半径为3,圆心O到直线l的距离为d,若直线l与⊙O没有公共点,则d为( ):
A.d
>3
B.d<3
C.d
≤3
D.d
=3
3、圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置关系是( ):
A.相离
B.相交
C.相切
D.相切或相交
A
C
3)若AB和⊙O相交,则
.
4、已知⊙O的半径为5,
圆心O到直线AB的距离为d,
根据条件填写d的范围:
1)若AB和⊙O相离,
则
;
2)若AB和⊙O相切,
则
;
d
>
5
d
=
5
d
<
5
0≤
5、已知⊙O的半径为r,
圆心O到直线AB的距离为3,
根据条件填写r的范围:
1)若AB和⊙O相切,
则
;
2)若AB和⊙O相交,
则
;
3)若AB和⊙O相离,
则
;
r
=3
r>
3
0<
r
<
3
2:圆的直径是13
,如果直线与圆心的距离分别是,
(1)
4.5;
(2)
6.5;
(3)
8.
那么直线和圆分别是什么位置关系?有几个公共点?
课本96页
随堂练习
(3)
当
d
=
8时,
有
d
>
r,因此圆与直线相离,没有公共点
当
r
=
6.5时,
有
d
=
r,因此圆与直线相切,
有一个公共点
当
d
=
4.5时,
有
d
<
r,
因此圆与直线相交,
有两个公共点
解:
r=6.5,设直线与圆心的距离为d
如图:∠AOB
=
30°M是OB上的一点,且OM
=5以M为圆心,以r
为半径的圆与
直线OA
有怎样的关系?为什么?
(1)r
=
2
;
(2)
r
=
4
;
(3)
r
=
2.5
.
C
O
B
A
M
5
30°
解:
过
M
作
MC⊥OA
于
C,在
Rt
△OMC
中,
∠AOB
=
30°
MC=
OM=
x5=2.5
1
2
1
2
即圆心
M
到OA的距离
d
=
2.5
.
因此⊙M
和
直线OA
相离.
(3)
当
r
=
2.5时,
因此⊙M
和直线
OA
相切.
(1)
当
r
=
2
时,
(2)
当
r
=
4
时,
因此⊙M
和直线O
A
相交.
2.5
有
d
>
r,
有
d
<
r,
有
d
=
r
,
典型例题
如图:M是OB上的一点,且OM
=5
以M为圆心,半径r=2.5作⊙M.
试问过O的射线
OA与OB所夹的锐角a取什么值时射线OA与
⊙M
(1)相离
(2)相切
(3)相交
?
C
O
B
A
M
5
a
2.5
例题的变式题
解:
过
M
作
MC⊥OA
于
C
1)当∠a
=
30°时,d=r=2.5
此时射线OA与⊙M相切
2)当
30°<
∠a
时
射线OA与⊙M相离
3)当
0
<
∠a
<30°时
射线OA与⊙M相交
<
90°
0
d>r
1
d=r
切点
切线
2
d
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
课堂小结
交点
割线
设⊙O的圆心O到直线的距离为d,半径为r,d.r是
方程(m+9)x2-
(m+6)
x
+1=0的两根,且直线与⊙O相切
时,求m的值?
方程
几何综合练习题
d=r
析:直线与⊙O相切
b2-4ac=0
[-(m+6)]2-4(m+9)=0
解得
m1=
-8
m2=
0
当m=-8时原方程
为x2+
2x+1=0
x1=x2=
-1
当m=0时原方程
为9x2-
6x+1=0
b2-4ac=
[-(m+6)]2-4(m+9)=0
解:由题意可得
x1=x2=
1
3
∴
m=0
(不符合题意舍去)
已知⊙O的半径r=7cm,直线l1
//
l2,且l1与⊙O相切,圆心O到l2的距离为9cm.求l1与l2的距离m.
o
。
l1
l2
A
B
C
l2
能力拓展
A.(-3,-4)
O
x
y
拓展:已知⊙A的直径为6,点A的坐标为(-3,-4),则x轴与⊙A的位置关系是_____,
y轴与⊙A的位置关系是_____。
B
C
4
3
相离
相切
-1
-1
.(-3,-4)
O
x
y
B
C
4
3
-1
-1
思考:若⊙A要与x轴相切,则⊙A该向上移动多少个单位?若⊙A要与x轴相交呢?
知识像一艘船
让它载着我们
驶向理想的
……
同课章节目录
