人教版数学八年级上册11.2.1三角形的内角 课件(共27张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.2.1三角形的内角 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 814.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 08:30:22 | ||
图片预览






文档简介
(共27张PPT)
11.2.1
三角形的内角
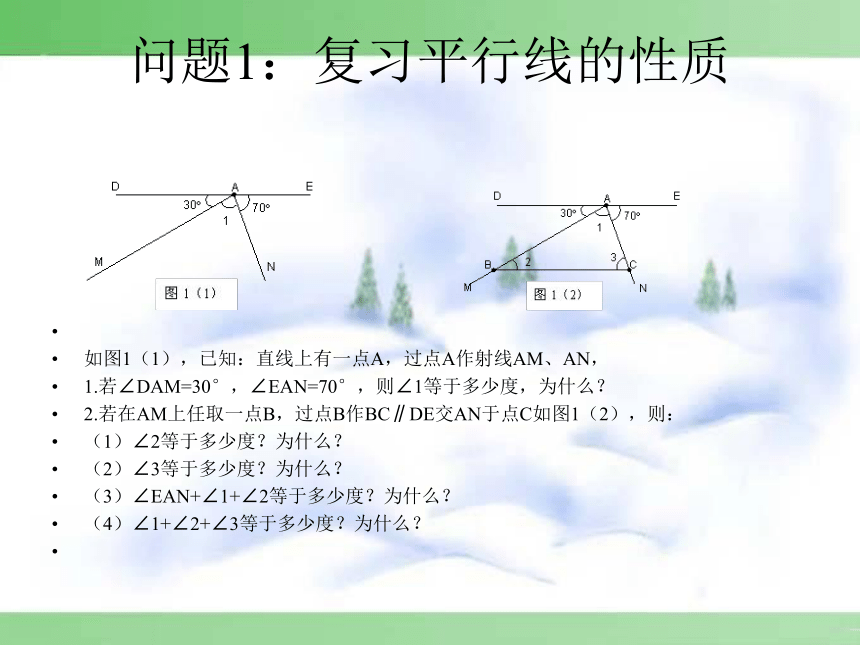
问题1:复习平行线的性质
?
如图1(1),已知:直线上有一点A,过点A作射线AM、AN,
1.若∠DAM=30°,∠EAN=70°,则∠1等于多少度,为什么?
2.若在AM上任取一点B,过点B作BC∥DE交AN于点C如图1(2),则:
(1)∠2等于多少度?为什么?
(2)∠3等于多少度?为什么?
(3)∠EAN+∠1+∠2等于多少度?为什么?
(4)∠1+∠2+∠3等于多少度?为什么?
?
问题2:小学学习的三角形三个内角的和等于180°,是如何证明的?
问题3:我们已经学习的与“180°”有关的知识有哪些?
探究活动
把准备好的三角形拿出来,并将它的内角剪下,试着拼拼看,三个内角的和是否为180°?有几种拼法?拼完后与小组成员交流,比一比看哪组的拼法最多。
把三个角拼在一起试试看?
从刚才拼角的过程你能想出证明的办法吗?
实践操作
问题4:证明三角形内角和定理:三角形的三个内角和等于180°?;
已知:如图2,.
求证:∠A+∠B+∠C=180°
F
2
1
E
C
B
A
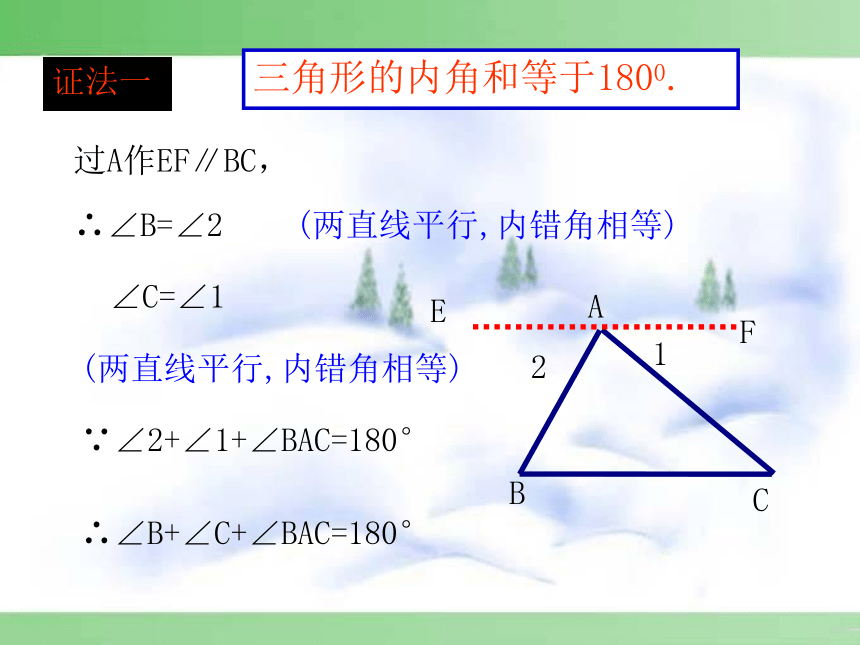
三角形的内角和等于1800.
过A作EF∥BC,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
证法一
2
1
E
D
C
B
A
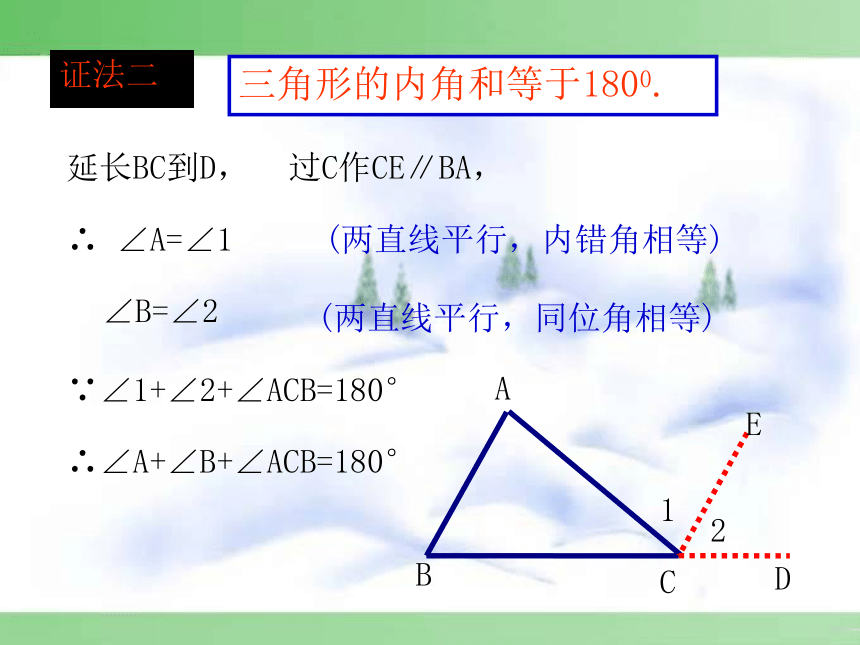
三角形的内角和等于1800.
延长BC到D,
过C作CE∥BA,
∴
∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
证法二
C
B
E
A
三角形的内角和等于1800.
过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
证法三
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
思路总结
(口答)下列各组角是同一个三角形的内角吗?为什么?
(2)60°,
40°,
90°
(3)30°,
60°,
50°
(1)3°,
150°,
27°
(是
)
(
不是)
(
不是)
巩固练习
(1)在△ABC中,∠A=35°,∠
B=43
°
则∠
C=
.
(2)在△ABC中,
∠A
:∠B:∠C=2:3:4
则∠A
=
∠
B=
∠
C=
.
(3)一个三角形中最多有
个直角?为什么?
(4)一个三角形中最多有
个钝角?为什么?
(5)一个三角形中至少有
个锐角?为什么?
(6)任意一个三角形中,最大的一个角的度数至少为
.
102
°
80
°
60
°
40
°
60°
2
1
1
应用新知
A
B
C
在直角三角形ABC中,∠C=90°,由三角形内角和定力,得,
∠A
+∠B+
∠C=180°
即
∠A
+∠B+
90°=180°,
所以
∠A
+∠B=
90°.
例题讲解1
也就是说,
直角三角形的两个锐角互余.
由三角形内角和定理可得:
有两个角互余的三角形是直角三角形。
直角三角形可以用符号“Rt△”表示,直角三角形ABC也可以写成Rt△ABC.
A
B
C
已知△ABC中,∠ABC=∠C=2∠A
,
BD是AC边上的高,求∠DBC的度数。
D
解:设∠A=x0,则∠ABC=∠C=2x0
∴x+2x+2x=180
(三角形内角和定理)
解得x=36
∴∠C=2×360=720
∴∠DBC=1800-900-720(三角形内角和定理)
在△BDC中,∵∠BDC=900
(三角形高的定义)
∴∠DBC=180
?
例题讲解2
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。求下面各题.
(1)∠DAC=_____
∠DAB=______
∠EBC=_______
∠CAB
=
______
A
(2)从C岛看A
、B两岛的视角∠C是多少?
50°
80°
40°
D
B
C
E
北
北
解:∵
AD∥BE
∴
∠DAB﹢∠ABE=180°
∴
∠ABE
=
180°-∠DAB
=
180°
-
80°
=100°
在△ABC中,∠C
=
180°
-
∠CAB
-
∠ABC
=
180°-30
°-60
°=90°
∴
∠ABC=∠ABE﹣∠CBE
30
°
=100°﹣40°=60°
例题讲解3
D
C
E
北
A
50°
∟
B
40
°
北
M
N
在△AMC中
∠AMC=90°,
∠MAC=50°
解:过点C画MN⊥AD分别交AD、BE于点M、N
1
2
例:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。
∴∠1=180
°-90°-50°
=40°
∵
AD∥BE
∴
∠AMC+
∠BNC
=180
°
∴
∠BNC
=90°
同理得∠2
=50°
∴
∠ACB
=180
°
-∠1
-∠2
=180
°-40°-50°
=90°
例题讲解3
B
D
C
E
北
A
1
2
50°
40°
解:
过点C画CF∥AD
∴
∠1=∠DAC=50
°,
F
∵
CF∥AD,
又AD
∥BE
∴
CF∥
BE
∴∠2=∠CBE
=40
°
∴
∠ACB=∠1﹢∠2
=50
°﹢
40
°
=90
°
例题讲解3
巩固练习
A
B
C
D
E
如图,∠C=
∠D=90°,AD与BC相交于点E,
∠CAE和∠DBE什么关系。
在Rt△ACE中,
∠CAE=90°-
∠AEC
在Rt△BDE中,
∠DBE=90°-
∠BED
∵
∠AEC=
∠BED(对顶角相等)
∴
∠CAE=
∠DBE
3.△ABC中,若∠A+∠B=∠C,则△ABC是(
)
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形
4.
一个三角形至少有(
)
A、一个锐角
B、两个锐角
C、一个钝角
D、一个直角
B
B
巩固练习
5.
如图△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,∠ADE=50°,
求∠BDC的度数.
A
B
C
D
E
解:
∵∠A=70°
∴∠ACB=180
°-∠A-∠B
=180°-70°-50°
=60°
∵DE//BC
∴∠B=∠ADE=50°
∵
CD平分∠ACB
巩固练习
2、在△ABC中,如果∠A=
∠B=
∠
C,那么△ABC是什么三角形?
解:设∠A=x°,
那么∠B=2x°,∠C=3x°
根据题意得:
解得
∴∠A=30°,∠B=60°,∠C=90°
所以△ABC是直角三角形
拓展与思考1
甲楼高16米,乙楼座落在甲楼的正北面,已知当地冬至中午12点,太阳光线与水平面夹角为450,如果甲楼的影子刚好不落在乙楼上,那么两楼的距离应是多少?
甲
乙
16米
450
?
450
16米
解:由题意知
A
B
C
∴BC=AB=16
答:两楼的距离是16米.
拓展与思考2
小结
1、三角形的内角和:三角形三个内角之和为180°
2、由三角形内角和等于180°,可得出
(1)直角三角形两锐角互余;
(2)一个三角形最多有一个直角或钝角;
(3)任意一个三角形中,最多有三个锐角,最少有两个锐角;
(4)一个三角形中至少有一个角小于或等于60°
复习旧知
一个三角形最多有
直角;
一个三角形最多有
钝角;
一个三角形中,最多有
锐角,最少有
锐角;
一个三角形中至少有一个角
小于或等于(
)
一个三角形中最大角至少是(
)
再见
11.2.1
三角形的内角
问题1:复习平行线的性质
?
如图1(1),已知:直线上有一点A,过点A作射线AM、AN,
1.若∠DAM=30°,∠EAN=70°,则∠1等于多少度,为什么?
2.若在AM上任取一点B,过点B作BC∥DE交AN于点C如图1(2),则:
(1)∠2等于多少度?为什么?
(2)∠3等于多少度?为什么?
(3)∠EAN+∠1+∠2等于多少度?为什么?
(4)∠1+∠2+∠3等于多少度?为什么?
?
问题2:小学学习的三角形三个内角的和等于180°,是如何证明的?
问题3:我们已经学习的与“180°”有关的知识有哪些?
探究活动
把准备好的三角形拿出来,并将它的内角剪下,试着拼拼看,三个内角的和是否为180°?有几种拼法?拼完后与小组成员交流,比一比看哪组的拼法最多。
把三个角拼在一起试试看?
从刚才拼角的过程你能想出证明的办法吗?
实践操作
问题4:证明三角形内角和定理:三角形的三个内角和等于180°?;
已知:如图2,.
求证:∠A+∠B+∠C=180°
F
2
1
E
C
B
A
三角形的内角和等于1800.
过A作EF∥BC,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
证法一
2
1
E
D
C
B
A
三角形的内角和等于1800.
延长BC到D,
过C作CE∥BA,
∴
∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
证法二
C
B
E
A
三角形的内角和等于1800.
过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
证法三
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
思路总结
(口答)下列各组角是同一个三角形的内角吗?为什么?
(2)60°,
40°,
90°
(3)30°,
60°,
50°
(1)3°,
150°,
27°
(是
)
(
不是)
(
不是)
巩固练习
(1)在△ABC中,∠A=35°,∠
B=43
°
则∠
C=
.
(2)在△ABC中,
∠A
:∠B:∠C=2:3:4
则∠A
=
∠
B=
∠
C=
.
(3)一个三角形中最多有
个直角?为什么?
(4)一个三角形中最多有
个钝角?为什么?
(5)一个三角形中至少有
个锐角?为什么?
(6)任意一个三角形中,最大的一个角的度数至少为
.
102
°
80
°
60
°
40
°
60°
2
1
1
应用新知
A
B
C
在直角三角形ABC中,∠C=90°,由三角形内角和定力,得,
∠A
+∠B+
∠C=180°
即
∠A
+∠B+
90°=180°,
所以
∠A
+∠B=
90°.
例题讲解1
也就是说,
直角三角形的两个锐角互余.
由三角形内角和定理可得:
有两个角互余的三角形是直角三角形。
直角三角形可以用符号“Rt△”表示,直角三角形ABC也可以写成Rt△ABC.
A
B
C
已知△ABC中,∠ABC=∠C=2∠A
,
BD是AC边上的高,求∠DBC的度数。
D
解:设∠A=x0,则∠ABC=∠C=2x0
∴x+2x+2x=180
(三角形内角和定理)
解得x=36
∴∠C=2×360=720
∴∠DBC=1800-900-720(三角形内角和定理)
在△BDC中,∵∠BDC=900
(三角形高的定义)
∴∠DBC=180
?
例题讲解2
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。求下面各题.
(1)∠DAC=_____
∠DAB=______
∠EBC=_______
∠CAB
=
______
A
(2)从C岛看A
、B两岛的视角∠C是多少?
50°
80°
40°
D
B
C
E
北
北
解:∵
AD∥BE
∴
∠DAB﹢∠ABE=180°
∴
∠ABE
=
180°-∠DAB
=
180°
-
80°
=100°
在△ABC中,∠C
=
180°
-
∠CAB
-
∠ABC
=
180°-30
°-60
°=90°
∴
∠ABC=∠ABE﹣∠CBE
30
°
=100°﹣40°=60°
例题讲解3
D
C
E
北
A
50°
∟
B
40
°
北
M
N
在△AMC中
∠AMC=90°,
∠MAC=50°
解:过点C画MN⊥AD分别交AD、BE于点M、N
1
2
例:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。
∴∠1=180
°-90°-50°
=40°
∵
AD∥BE
∴
∠AMC+
∠BNC
=180
°
∴
∠BNC
=90°
同理得∠2
=50°
∴
∠ACB
=180
°
-∠1
-∠2
=180
°-40°-50°
=90°
例题讲解3
B
D
C
E
北
A
1
2
50°
40°
解:
过点C画CF∥AD
∴
∠1=∠DAC=50
°,
F
∵
CF∥AD,
又AD
∥BE
∴
CF∥
BE
∴∠2=∠CBE
=40
°
∴
∠ACB=∠1﹢∠2
=50
°﹢
40
°
=90
°
例题讲解3
巩固练习
A
B
C
D
E
如图,∠C=
∠D=90°,AD与BC相交于点E,
∠CAE和∠DBE什么关系。
在Rt△ACE中,
∠CAE=90°-
∠AEC
在Rt△BDE中,
∠DBE=90°-
∠BED
∵
∠AEC=
∠BED(对顶角相等)
∴
∠CAE=
∠DBE
3.△ABC中,若∠A+∠B=∠C,则△ABC是(
)
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形
4.
一个三角形至少有(
)
A、一个锐角
B、两个锐角
C、一个钝角
D、一个直角
B
B
巩固练习
5.
如图△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,∠ADE=50°,
求∠BDC的度数.
A
B
C
D
E
解:
∵∠A=70°
∴∠ACB=180
°-∠A-∠B
=180°-70°-50°
=60°
∵DE//BC
∴∠B=∠ADE=50°
∵
CD平分∠ACB
巩固练习
2、在△ABC中,如果∠A=
∠B=
∠
C,那么△ABC是什么三角形?
解:设∠A=x°,
那么∠B=2x°,∠C=3x°
根据题意得:
解得
∴∠A=30°,∠B=60°,∠C=90°
所以△ABC是直角三角形
拓展与思考1
甲楼高16米,乙楼座落在甲楼的正北面,已知当地冬至中午12点,太阳光线与水平面夹角为450,如果甲楼的影子刚好不落在乙楼上,那么两楼的距离应是多少?
甲
乙
16米
450
?
450
16米
解:由题意知
A
B
C
∴BC=AB=16
答:两楼的距离是16米.
拓展与思考2
小结
1、三角形的内角和:三角形三个内角之和为180°
2、由三角形内角和等于180°,可得出
(1)直角三角形两锐角互余;
(2)一个三角形最多有一个直角或钝角;
(3)任意一个三角形中,最多有三个锐角,最少有两个锐角;
(4)一个三角形中至少有一个角小于或等于60°
复习旧知
一个三角形最多有
直角;
一个三角形最多有
钝角;
一个三角形中,最多有
锐角,最少有
锐角;
一个三角形中至少有一个角
小于或等于(
)
一个三角形中最大角至少是(
)
再见
