人教版数学八年级上册11.2.2三角形的外角课件(共20张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.2.2三角形的外角课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
11.2.2
三角形的外角
2、在ABC中,
(1)∠C=90°,∠A=30
°
,则∠B=
;
(2)∠A=50
°
,∠B=∠C,则∠B=
.
1、三角形三个内角的和等于多少度?
3、在△ABC中,
∠A:∠B:∠C=2:3:4.
则∠A=
,
∠B=
,∠C=
.
40°
60°
80°
65°
60°
怎么验证呢?
A
B
C
D
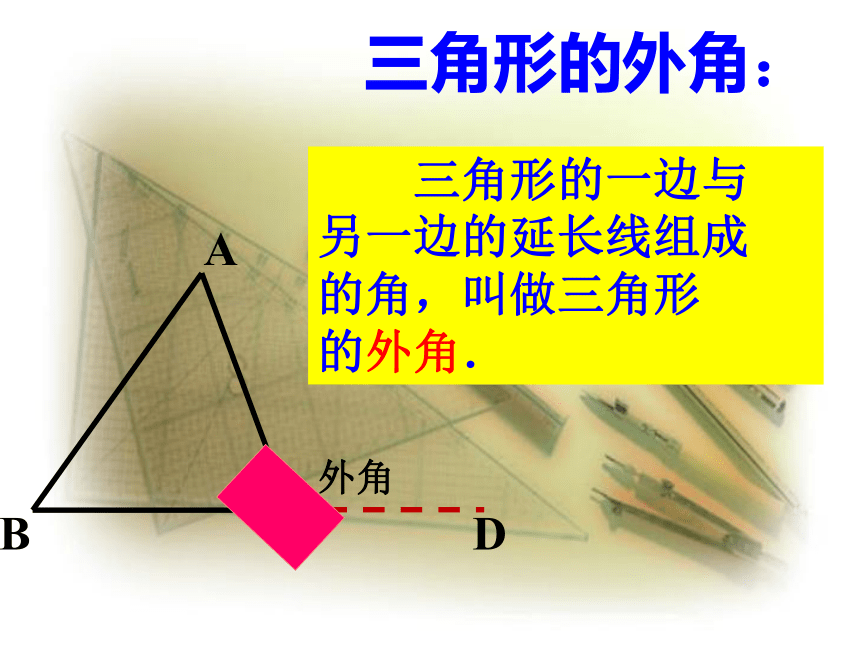
三角形的外角:
三角形的一边与
另一边的延长线组成
的角,叫做三角形
的外角.
外角
外角
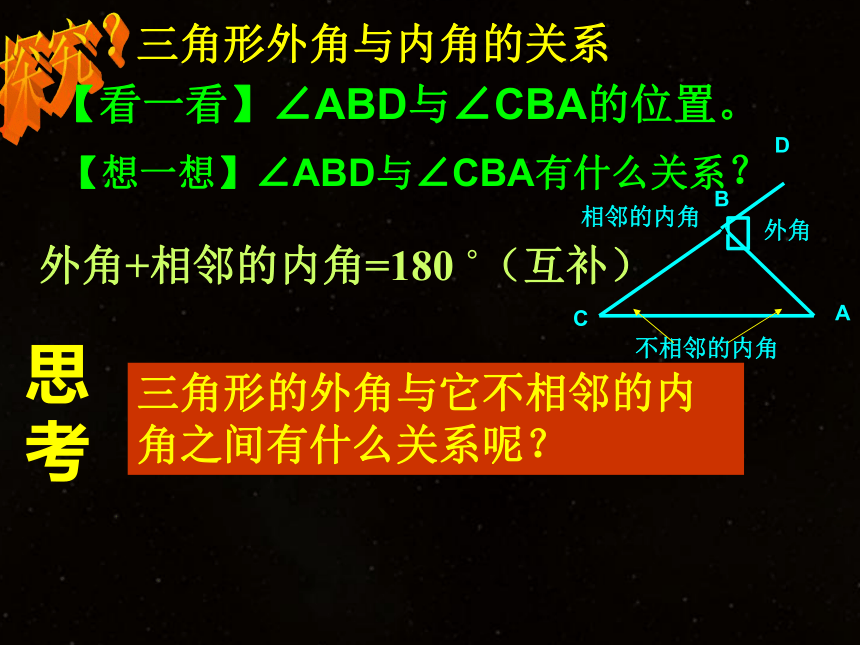
三角形外角与内角的关系
外角+相邻的内角=180
?(互补)
相邻的内角
不相邻的内角
思考
三角形的外角与它不相邻的内角之间有什么关系呢?
A
B
C
D
【看一看】∠ABD与∠CBA的位置。
【想一想】∠ABD与∠CBA有什么关系?
探究
A
D
C
B
①∠CBD=∠C+∠A
将∠A、∠C剪下拼在∠CBD的位置,
同学之间相互交流,发现什么结论?
动动手
E
∵
∠ABC
+
∠CBD=
180
°
又∵
∠ABC+
∠C+
∠A=
180
°
∴
∠CBD=
∠C+
∠A
证明(一)
证明(二):
过B点作
BE∥AC
∴
∠EBD
=
∠A
∠CBE
=
∠C
∴
∠CBD
=
∠CBE+
∠EBD
=
∠C+
∠A
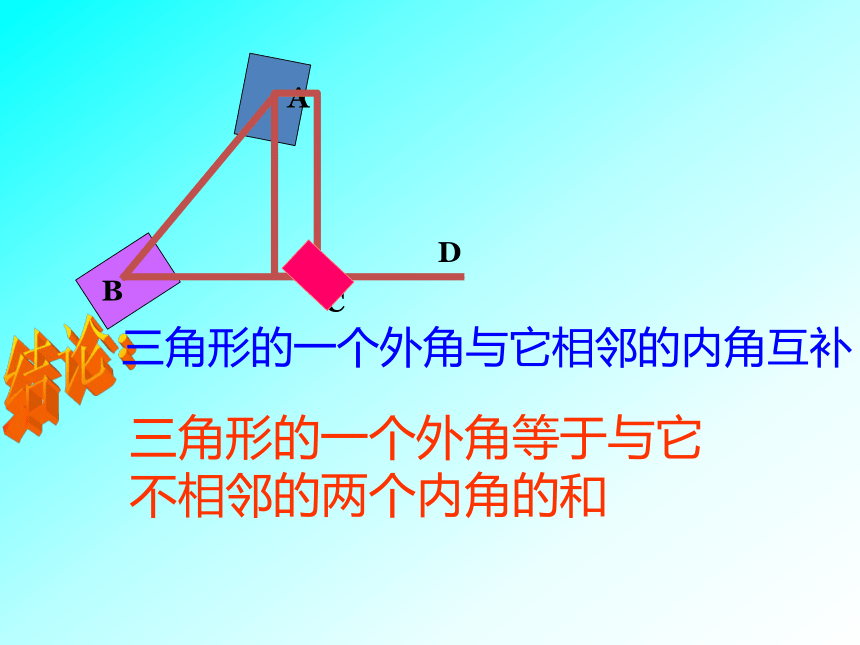
三角形的一个外角等于与它不相邻的两个内角的和
三角形的一个外角等于与它不相邻的两个内角的和
三角形的一个外角与它相邻的内角互补
A
C
B
D
∠ACD
∠A
(填写不等号);
∠ACD
∠B
(填写不等号)
结论:三角形的一个外角大于与它不相邻的任何一个内角.
D
A
C
B
>
>
你选谁
?
议一议议一议
三角形的外角与内角的关系:
1、三角形的一个外角与它相邻的内角
;
2、三角形的一个外角
与它不相邻的
两个内角的和;
3、三角形的一个外角
任何一个与它
不相邻的内角。
等于
大于
互补
快速抢答,看谁答得又快又准。
∠1=_________+__________
∠2=_________+__________
∠2________∠3,
∠2________∠4
练一练练一练
A
B
C
D
2°
3
4
1
∠CAD
∠C
∠3
∠4
>
>
2、求下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
练一练练一练
90°
95°
85°
3、把图中∠1、
∠2、
∠3按由大到小的顺序排列
3
2
1
A
B
C
D
E
练一练练一练
∠1>∠2>∠3
找出△ABC的所有外角,共有几个外角?
共有6个外角:
F
I
E
G
D
H
B
C
A
∠1,
∠2,
∠3,
∠4,
∠5,
∠6。
1
2
3
6
4
5
∠1+∠2
+∠3就是△ABC的外角和
∠1+∠2
+∠3
=
?
从哪些途径探究这个结果?
议一议
3
2
1
A
B
C
5
6
4
三角形的外角和等于360°
方法1
方法2
go
A
B
C
1
2
3
∠2+
∠ABC=180°
∠3+
∠ACB=180°
三个式子相加得到
∠1+
∠2+
∠3+
∠BAC+
∠ABC+∠ACB=540°
而∠BAC+
∠ABC+∠ACB=180°
∠1+
∠2+
∠3=360°
∠1+
∠BAC=180°
解:
解:过A作AD平行于BC
∠3=
∠4
B
C
1
2
3
4
A
∠2=
∠BAD
所以,
∠1+
∠2+
∠3=
∠1+
∠4+
∠BAD=360°
两直线平行,同位角相等
D
∠2+
∠
3=
∠
4+∠BAD
1.三角形的外角和是指三角形所有外角的和
2.三角形的外角和等于它内角和的2倍。
3.三角形的一个外角等于两个内角的和。
4、三角形的一个外角等于与它不相邻的两个内角的和。
5.三角形的一个外角大于任何一个内角。
6.三角形的一个外角大于任何一个不相邻的内角
3.三角形的一个外角大于任何一个与它不相邻的内角.
2.三角形的一个外角等于与它不相邻的两个内角的和;
1.三角形的一个外角与它相邻的内角互补;
三角形的外角与内角的关系:
小结
学一学
例1:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
(1)解:∵∠B+∠BAD=∠ADC
∴∠B+∠BAD=80°
又∵∠B=∠BAD
∴∠B=1/2∠ADC=40°
学一学
例1:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
(2)解法1:∵∠DAC+∠BAD=∠BAC
∴∠DAC=∠BAC-∠BAD
=70°-40°=30°
又∵∠C=180°-∠ADC-∠DAC
∴∠C=180°-80°-30°=70°
学一学
例1:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
(2)解法2:∵∠B+∠BAC+∠C=180°
∴∠C=180°-∠B-∠BAC
=180°-40°-70°=70°
11.2.2
三角形的外角
2、在ABC中,
(1)∠C=90°,∠A=30
°
,则∠B=
;
(2)∠A=50
°
,∠B=∠C,则∠B=
.
1、三角形三个内角的和等于多少度?
3、在△ABC中,
∠A:∠B:∠C=2:3:4.
则∠A=
,
∠B=
,∠C=
.
40°
60°
80°
65°
60°
怎么验证呢?
A
B
C
D
三角形的外角:
三角形的一边与
另一边的延长线组成
的角,叫做三角形
的外角.
外角
外角
三角形外角与内角的关系
外角+相邻的内角=180
?(互补)
相邻的内角
不相邻的内角
思考
三角形的外角与它不相邻的内角之间有什么关系呢?
A
B
C
D
【看一看】∠ABD与∠CBA的位置。
【想一想】∠ABD与∠CBA有什么关系?
探究
A
D
C
B
①∠CBD=∠C+∠A
将∠A、∠C剪下拼在∠CBD的位置,
同学之间相互交流,发现什么结论?
动动手
E
∵
∠ABC
+
∠CBD=
180
°
又∵
∠ABC+
∠C+
∠A=
180
°
∴
∠CBD=
∠C+
∠A
证明(一)
证明(二):
过B点作
BE∥AC
∴
∠EBD
=
∠A
∠CBE
=
∠C
∴
∠CBD
=
∠CBE+
∠EBD
=
∠C+
∠A
三角形的一个外角等于与它不相邻的两个内角的和
三角形的一个外角等于与它不相邻的两个内角的和
三角形的一个外角与它相邻的内角互补
A
C
B
D
∠ACD
∠A
(填写不等号);
∠ACD
∠B
(填写不等号)
结论:三角形的一个外角大于与它不相邻的任何一个内角.
D
A
C
B
>
>
你选谁
?
议一议议一议
三角形的外角与内角的关系:
1、三角形的一个外角与它相邻的内角
;
2、三角形的一个外角
与它不相邻的
两个内角的和;
3、三角形的一个外角
任何一个与它
不相邻的内角。
等于
大于
互补
快速抢答,看谁答得又快又准。
∠1=_________+__________
∠2=_________+__________
∠2________∠3,
∠2________∠4
练一练练一练
A
B
C
D
2°
3
4
1
∠CAD
∠C
∠3
∠4
>
>
2、求下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
练一练练一练
90°
95°
85°
3、把图中∠1、
∠2、
∠3按由大到小的顺序排列
3
2
1
A
B
C
D
E
练一练练一练
∠1>∠2>∠3
找出△ABC的所有外角,共有几个外角?
共有6个外角:
F
I
E
G
D
H
B
C
A
∠1,
∠2,
∠3,
∠4,
∠5,
∠6。
1
2
3
6
4
5
∠1+∠2
+∠3就是△ABC的外角和
∠1+∠2
+∠3
=
?
从哪些途径探究这个结果?
议一议
3
2
1
A
B
C
5
6
4
三角形的外角和等于360°
方法1
方法2
go
A
B
C
1
2
3
∠2+
∠ABC=180°
∠3+
∠ACB=180°
三个式子相加得到
∠1+
∠2+
∠3+
∠BAC+
∠ABC+∠ACB=540°
而∠BAC+
∠ABC+∠ACB=180°
∠1+
∠2+
∠3=360°
∠1+
∠BAC=180°
解:
解:过A作AD平行于BC
∠3=
∠4
B
C
1
2
3
4
A
∠2=
∠BAD
所以,
∠1+
∠2+
∠3=
∠1+
∠4+
∠BAD=360°
两直线平行,同位角相等
D
∠2+
∠
3=
∠
4+∠BAD
1.三角形的外角和是指三角形所有外角的和
2.三角形的外角和等于它内角和的2倍。
3.三角形的一个外角等于两个内角的和。
4、三角形的一个外角等于与它不相邻的两个内角的和。
5.三角形的一个外角大于任何一个内角。
6.三角形的一个外角大于任何一个不相邻的内角
3.三角形的一个外角大于任何一个与它不相邻的内角.
2.三角形的一个外角等于与它不相邻的两个内角的和;
1.三角形的一个外角与它相邻的内角互补;
三角形的外角与内角的关系:
小结
学一学
例1:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
(1)解:∵∠B+∠BAD=∠ADC
∴∠B+∠BAD=80°
又∵∠B=∠BAD
∴∠B=1/2∠ADC=40°
学一学
例1:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
(2)解法1:∵∠DAC+∠BAD=∠BAC
∴∠DAC=∠BAC-∠BAD
=70°-40°=30°
又∵∠C=180°-∠ADC-∠DAC
∴∠C=180°-80°-30°=70°
学一学
例1:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
(2)解法2:∵∠B+∠BAC+∠C=180°
∴∠C=180°-∠B-∠BAC
=180°-40°-70°=70°
