数学:同步授课课件 11.2.1《三角形全等的判定(sss)》(人教实验版八年级上)
文档属性
| 名称 | 数学:同步授课课件 11.2.1《三角形全等的判定(sss)》(人教实验版八年级上) |  | |
| 格式 | zip | ||
| 文件大小 | 701.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-23 12:33:33 | ||
图片预览


文档简介
(共16张PPT)
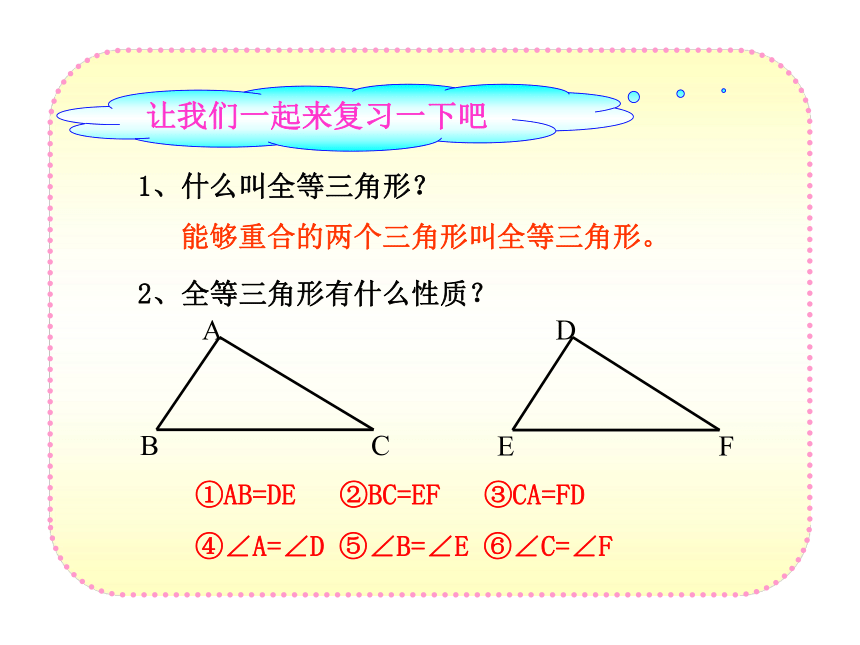
让我们一起来复习一下吧
①AB=DE ②BC=EF ③CA=FD
④∠A=∠D ⑤∠B=∠E ⑥∠C=∠F
A
B
C
D
E
F
1、什么叫全等三角形?
能够重合的两个三角形叫全等三角形。
2、全等三角形有什么性质?
问题一:
根据上面的结论,两个三角形全等,它们的三个角、三条边分别对应相等,那么反过来,如果两个三角形中上述六个元素对应相等,是否一定全等?
问题二:
两个三角形全等,是否一定需要六个条件呢?如果只满足上述一部分条件,是否我们也能说明他们全等?
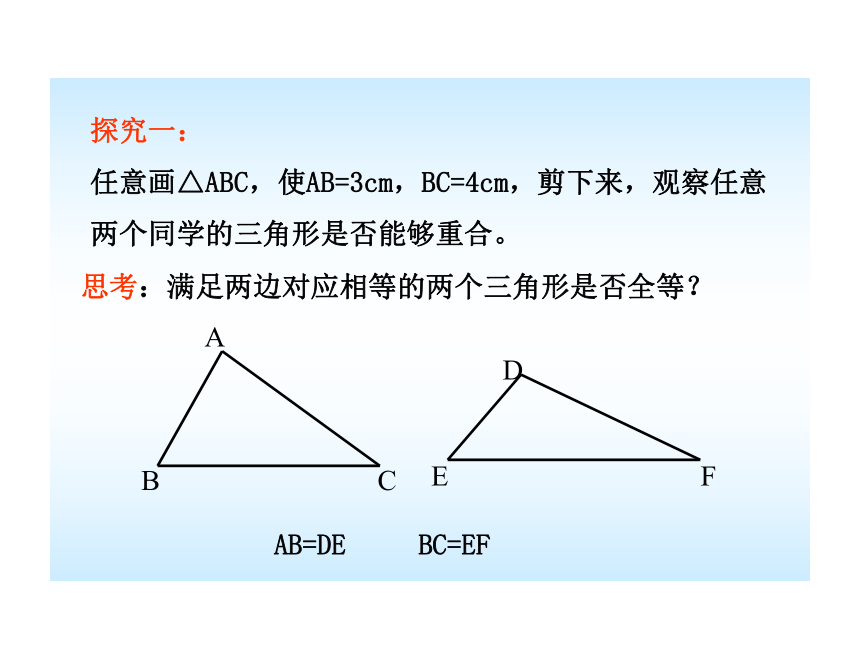
探究一:
任意画△ABC,使AB=3cm,BC=4cm,剪下来,观察任意两个同学的三角形是否能够重合。
AB=DE BC=EF
思考:满足两边对应相等的两个三角形是否全等?
A
B
C
D
E
F
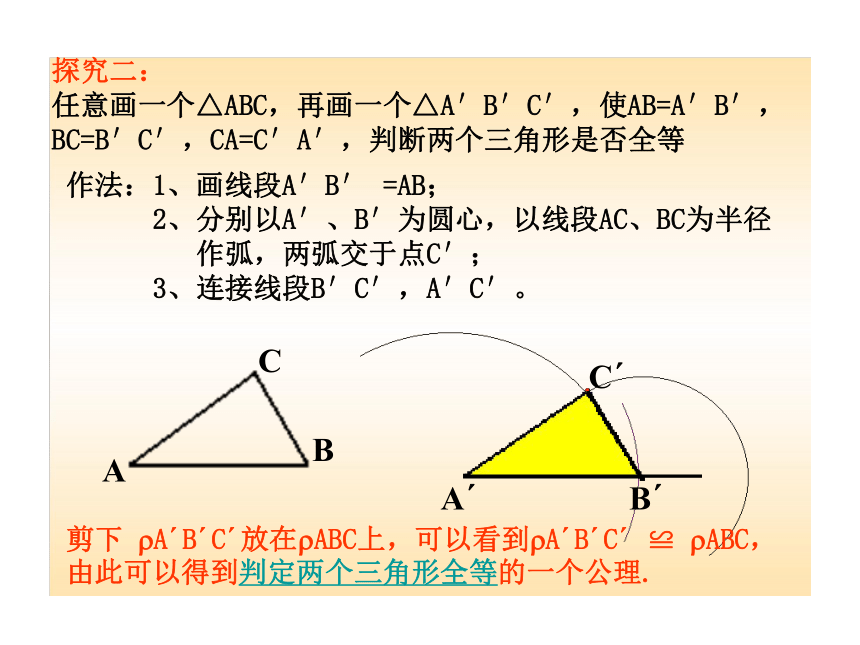
探究二:
任意画一个△ABC,再画一个△A′B′C′,使AB=A′B′,BC=B′C′,CA=C′A′,判断两个三角形是否全等
作法:1、画线段A′B′ =AB;
2、分别以A′、B′为圆心,以线段AC、BC为半径
作弧,两弧交于点C′;
3、连接线段B′C′,A′C′。
A
B
C
B
C
A
剪下 A B C 放在 ABC上,可以看到 A B C ≌ ABC,由此可以得到判定两个三角形全等的一个公理.
A
B
C
D
E
F
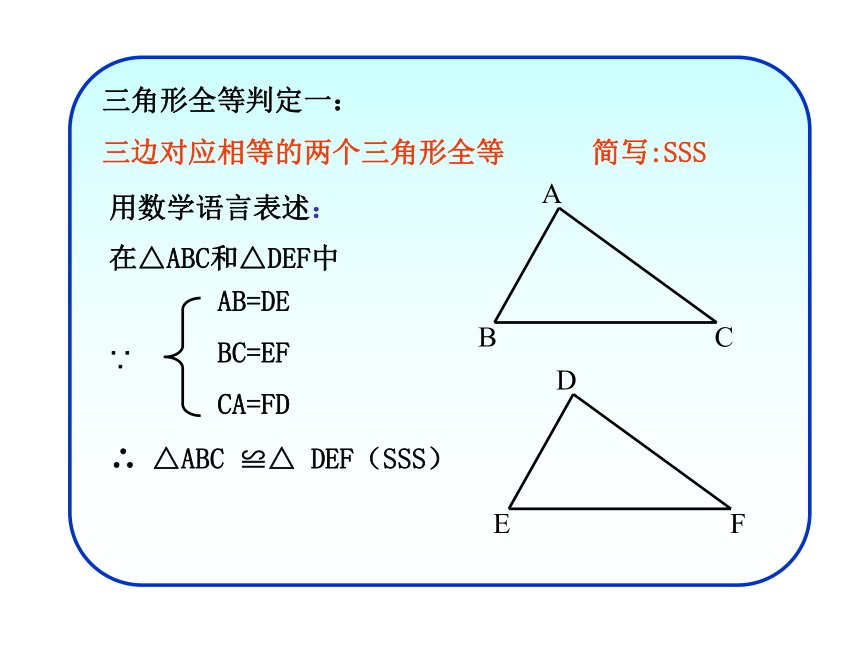
用数学语言表述:
在△ABC和△DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
三角形全等判定一:
三边对应相等的两个三角形全等 简写:SSS
∵
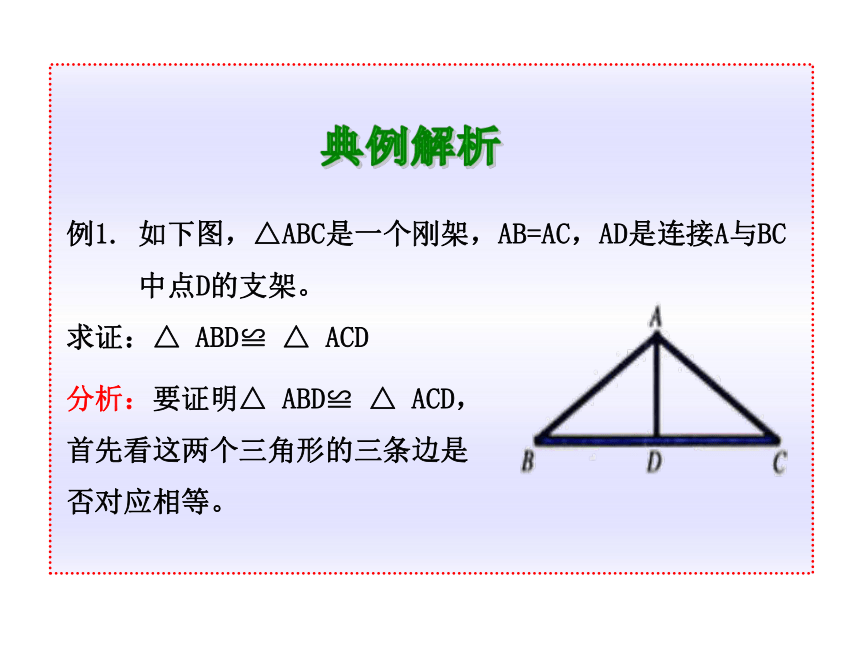
例1. 如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC
中点D的支架。
求证:△ ABD≌ △ ACD
分析:要证明△ ABD≌ △ ACD,
首先看这两个三角形的三条边是
否对应相等。
证明:∵ D是BC的中点
∴ BD=CD
在△ABC和△ACD中,
AB=AC (已知)
BD=CD (已证)
AD=AD (公共边)
∴ △ABD ≌ △ACD (SSS)
∵
①准备条件:证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中
摆出三个条件用大括号括起来
写出全等结论
证明的书写步骤:
A
B
C
D
△ABC≌ ( )
解:△ABC≌△DCB
理由如下:
AB = CD
AC = DB
=
2、如图,D、F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD ,
还需要条件
A
E
B D F C
1、如图,AB=CD,AC=BD,△ABC和△DCB是否全等?
△DCB
BC
CB
BF=CD
或BD=CF
SSS
如图,在四边形ABCD中AB=CD,AD=BC,
则∠A= ∠C请说明理由。
A
B
C
D
解:在 ABD和 CDB中
AB=CD (已知)
AD=BC (已知)
BD=DB
(公共边)
(SSS)
∴ ABD ≌ CDB
∴ ∠A= ∠C( )
全等三角形的对应角相等
开动你的脑筋,你一定行!
我们利用前面的结论,你可以得到作一个角等于已知角的方法吗?
已知:∠AOB
求作:∠A′O′B′=∠AOB
O
A
B
C
D
O′
A′
B′
C′
D′
作法:1、以点O为圆心,任意长为半径画弧,分别交OA,
OB于点C、D;
2、画一条射线O′A′,以点O′为圆心,OC长为半
径画弧,交O′A′于点C′;
3、以点C′为圆心,CD长为半径画弧,与第2步中
所画的弧交于点D′;
4、过点D′画射线O′B′,则∠A′O′B′=∠AOB
2.三边对应相等的两个三角形全等(边边边或SSS)。
1.知道三角形三条边的长度怎样画三角形。
3.体验分类讨论的数学思想。
4.初步学会理解证明的思路。
说一说
这节课我的收获是……
让我们一起来复习一下吧
①AB=DE ②BC=EF ③CA=FD
④∠A=∠D ⑤∠B=∠E ⑥∠C=∠F
A
B
C
D
E
F
1、什么叫全等三角形?
能够重合的两个三角形叫全等三角形。
2、全等三角形有什么性质?
问题一:
根据上面的结论,两个三角形全等,它们的三个角、三条边分别对应相等,那么反过来,如果两个三角形中上述六个元素对应相等,是否一定全等?
问题二:
两个三角形全等,是否一定需要六个条件呢?如果只满足上述一部分条件,是否我们也能说明他们全等?
探究一:
任意画△ABC,使AB=3cm,BC=4cm,剪下来,观察任意两个同学的三角形是否能够重合。
AB=DE BC=EF
思考:满足两边对应相等的两个三角形是否全等?
A
B
C
D
E
F
探究二:
任意画一个△ABC,再画一个△A′B′C′,使AB=A′B′,BC=B′C′,CA=C′A′,判断两个三角形是否全等
作法:1、画线段A′B′ =AB;
2、分别以A′、B′为圆心,以线段AC、BC为半径
作弧,两弧交于点C′;
3、连接线段B′C′,A′C′。
A
B
C
B
C
A
剪下 A B C 放在 ABC上,可以看到 A B C ≌ ABC,由此可以得到判定两个三角形全等的一个公理.
A
B
C
D
E
F
用数学语言表述:
在△ABC和△DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
三角形全等判定一:
三边对应相等的两个三角形全等 简写:SSS
∵
例1. 如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC
中点D的支架。
求证:△ ABD≌ △ ACD
分析:要证明△ ABD≌ △ ACD,
首先看这两个三角形的三条边是
否对应相等。
证明:∵ D是BC的中点
∴ BD=CD
在△ABC和△ACD中,
AB=AC (已知)
BD=CD (已证)
AD=AD (公共边)
∴ △ABD ≌ △ACD (SSS)
∵
①准备条件:证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中
摆出三个条件用大括号括起来
写出全等结论
证明的书写步骤:
A
B
C
D
△ABC≌ ( )
解:△ABC≌△DCB
理由如下:
AB = CD
AC = DB
=
2、如图,D、F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD ,
还需要条件
A
E
B D F C
1、如图,AB=CD,AC=BD,△ABC和△DCB是否全等?
△DCB
BC
CB
BF=CD
或BD=CF
SSS
如图,在四边形ABCD中AB=CD,AD=BC,
则∠A= ∠C请说明理由。
A
B
C
D
解:在 ABD和 CDB中
AB=CD (已知)
AD=BC (已知)
BD=DB
(公共边)
(SSS)
∴ ABD ≌ CDB
∴ ∠A= ∠C( )
全等三角形的对应角相等
开动你的脑筋,你一定行!
我们利用前面的结论,你可以得到作一个角等于已知角的方法吗?
已知:∠AOB
求作:∠A′O′B′=∠AOB
O
A
B
C
D
O′
A′
B′
C′
D′
作法:1、以点O为圆心,任意长为半径画弧,分别交OA,
OB于点C、D;
2、画一条射线O′A′,以点O′为圆心,OC长为半
径画弧,交O′A′于点C′;
3、以点C′为圆心,CD长为半径画弧,与第2步中
所画的弧交于点D′;
4、过点D′画射线O′B′,则∠A′O′B′=∠AOB
2.三边对应相等的两个三角形全等(边边边或SSS)。
1.知道三角形三条边的长度怎样画三角形。
3.体验分类讨论的数学思想。
4.初步学会理解证明的思路。
说一说
这节课我的收获是……
