数学:同步授课课件 11.2.2《三角形全等的判定(sas)》(人教实验版八年级上)
文档属性
| 名称 | 数学:同步授课课件 11.2.2《三角形全等的判定(sas)》(人教实验版八年级上) |  | |
| 格式 | zip | ||
| 文件大小 | 589.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-23 12:33:33 | ||
图片预览



文档简介
(共12张PPT)
还记得作一个角等于已知角的方法吗?
做一做:先任意画出△ABC.再画一个△A′B′C′,使A′B′=AB, A′C′=AC,∠A′=∠A.(即有两边和它们的夹角相等).把画好的△A′B′C′剪下,放到△ABC上,它们全等吗
画法:
2. 在射线A′M上截取A′B′=AB
3. 在射线A′N上截取A′C′=AC
1. 画∠MA′N=∠A
4. 连接B′C′
∴△A′B′C′就是所求的三角形
探究的结果反映了什么规律
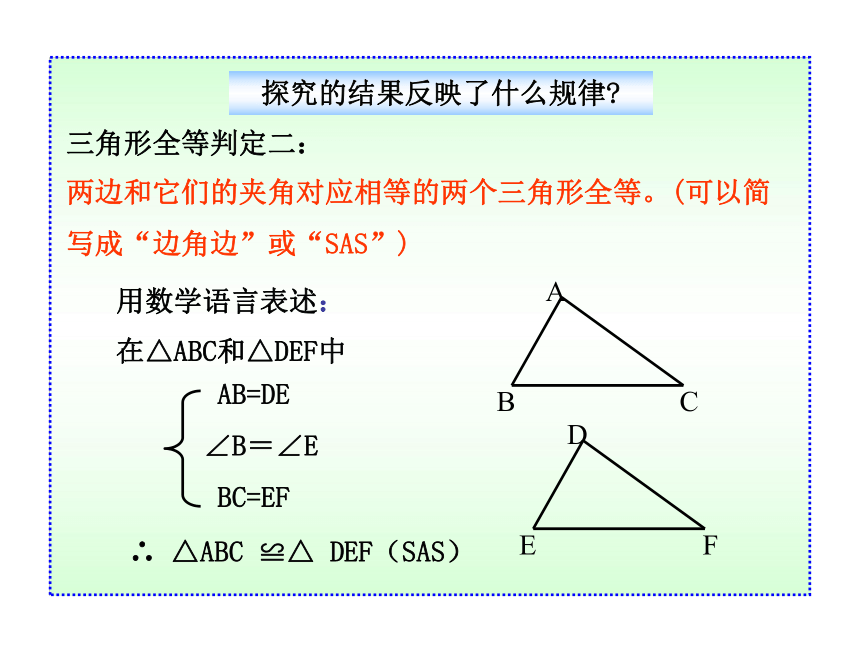
三角形全等判定二:
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
用数学语言表述:
A
B
C
D
E
F
在△ABC和△DEF中
∴ △ABC ≌△ DEF(SAS)
AB=DE
∠B=∠E
BC=EF
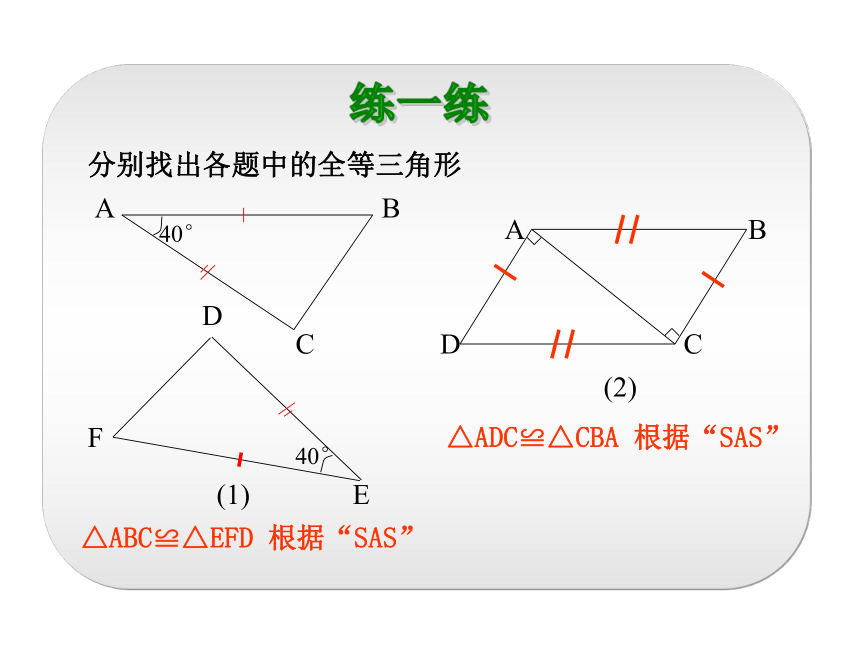
分别找出各题中的全等三角形
A
B
C
40°
D
E
F
(1)
△ABC≌△EFD 根据“SAS”
△ADC≌△CBA 根据“SAS”
40°
D
C
A
B
(2)
图 1
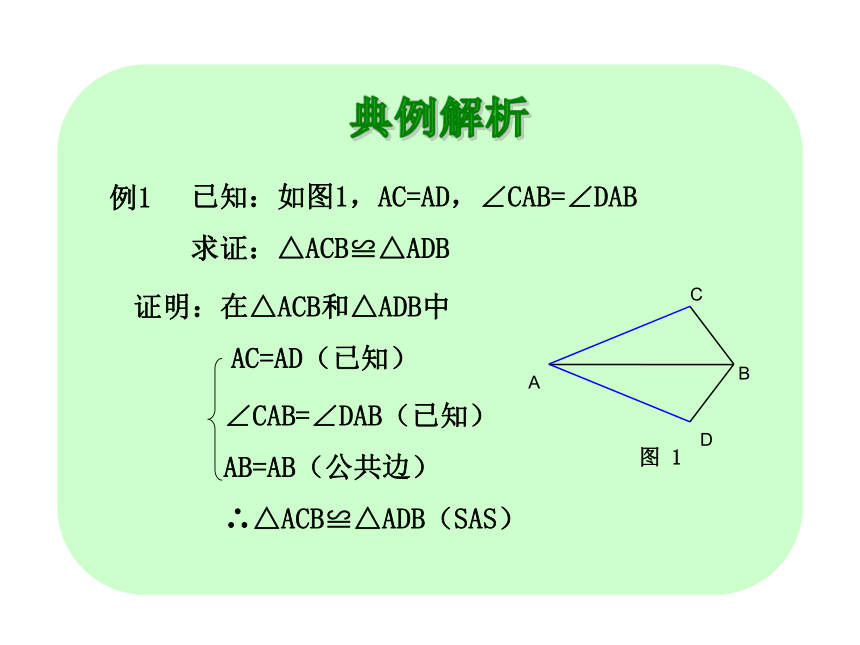
已知:如图1,AC=AD,∠CAB=∠DAB
求证:△ACB≌△ADB
AC=AD(已知)
∠CAB=∠DAB(已知)
AB=AB(公共边)
∴△ACB≌△ADB(SAS)
例1
证明:在△ACB和△ADB中
A
B
C
D
如图,修补一块玻璃,问取哪一块玻璃可以使得这块新玻璃与原来的完全一样?
Ⅰ
Ⅱ
Ⅲ
知识应用
分析:带Ⅲ去,可以根据SAS得到与原三角形全等的一个三角形
已知:AD=CD,BD平分∠ADC
求证:(1)∠A=∠C
(2)AB=BC
A
B
C
D
1
2
归纳:证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到。
分析:可先证△ABD≌△CBD(SAS)
再根据全等三角形的性质证角或线段相等。
已知:如图,AD∥BC,AD=CB
求证:△ADC≌△CBA
AD=CB(已知)
∠1=∠2(已知)
AC=CA (公共边)
∴△ADC≌△CBA(SAS)
证明:∵AD∥BC
∴∠1=∠2(两直线平行,内错角相等)
在△DAC和△BCA中
D
C
1
A
2
B
开动你的脑筋,你一定行!
用符号语言表达为:
A
B
C
D
E
F
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。
(简写成“边角边”或“SAS”)
小结
这节课我的收获是……
说一说
还记得作一个角等于已知角的方法吗?
做一做:先任意画出△ABC.再画一个△A′B′C′,使A′B′=AB, A′C′=AC,∠A′=∠A.(即有两边和它们的夹角相等).把画好的△A′B′C′剪下,放到△ABC上,它们全等吗
画法:
2. 在射线A′M上截取A′B′=AB
3. 在射线A′N上截取A′C′=AC
1. 画∠MA′N=∠A
4. 连接B′C′
∴△A′B′C′就是所求的三角形
探究的结果反映了什么规律
三角形全等判定二:
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
用数学语言表述:
A
B
C
D
E
F
在△ABC和△DEF中
∴ △ABC ≌△ DEF(SAS)
AB=DE
∠B=∠E
BC=EF
分别找出各题中的全等三角形
A
B
C
40°
D
E
F
(1)
△ABC≌△EFD 根据“SAS”
△ADC≌△CBA 根据“SAS”
40°
D
C
A
B
(2)
图 1
已知:如图1,AC=AD,∠CAB=∠DAB
求证:△ACB≌△ADB
AC=AD(已知)
∠CAB=∠DAB(已知)
AB=AB(公共边)
∴△ACB≌△ADB(SAS)
例1
证明:在△ACB和△ADB中
A
B
C
D
如图,修补一块玻璃,问取哪一块玻璃可以使得这块新玻璃与原来的完全一样?
Ⅰ
Ⅱ
Ⅲ
知识应用
分析:带Ⅲ去,可以根据SAS得到与原三角形全等的一个三角形
已知:AD=CD,BD平分∠ADC
求证:(1)∠A=∠C
(2)AB=BC
A
B
C
D
1
2
归纳:证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到。
分析:可先证△ABD≌△CBD(SAS)
再根据全等三角形的性质证角或线段相等。
已知:如图,AD∥BC,AD=CB
求证:△ADC≌△CBA
AD=CB(已知)
∠1=∠2(已知)
AC=CA (公共边)
∴△ADC≌△CBA(SAS)
证明:∵AD∥BC
∴∠1=∠2(两直线平行,内错角相等)
在△DAC和△BCA中
D
C
1
A
2
B
开动你的脑筋,你一定行!
用符号语言表达为:
A
B
C
D
E
F
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。
(简写成“边角边”或“SAS”)
小结
这节课我的收获是……
说一说
