北师大版八年级数学上册 2.1认识无理数课件(共23张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 2.1认识无理数课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 418.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 09:02:08 | ||
图片预览




文档简介
(共23张PPT)
在数学天地里,重要的不是我们知道什么,而是我们怎么知道——
数学家寄语
毕达哥拉斯
无理数(1)
整数
正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…
分数
正分数:如
,
,5.2,
…
负分数如
,
,-3.5,…
有理数
回顾
&
思考
?
什么叫有理数?
分数与有限小数和无限循环小数可以互化
所以我们把有限小数和无限循环小数都看作分数
回顾
&
思考
?
有理数:整数和分数统称为有理数。
例如:
分数
有限小数
无限循环小数
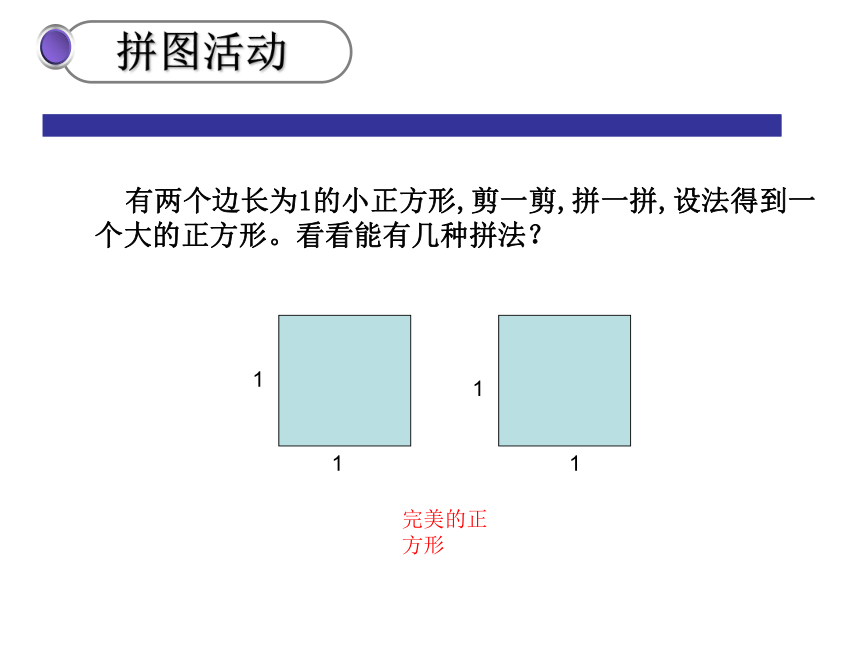
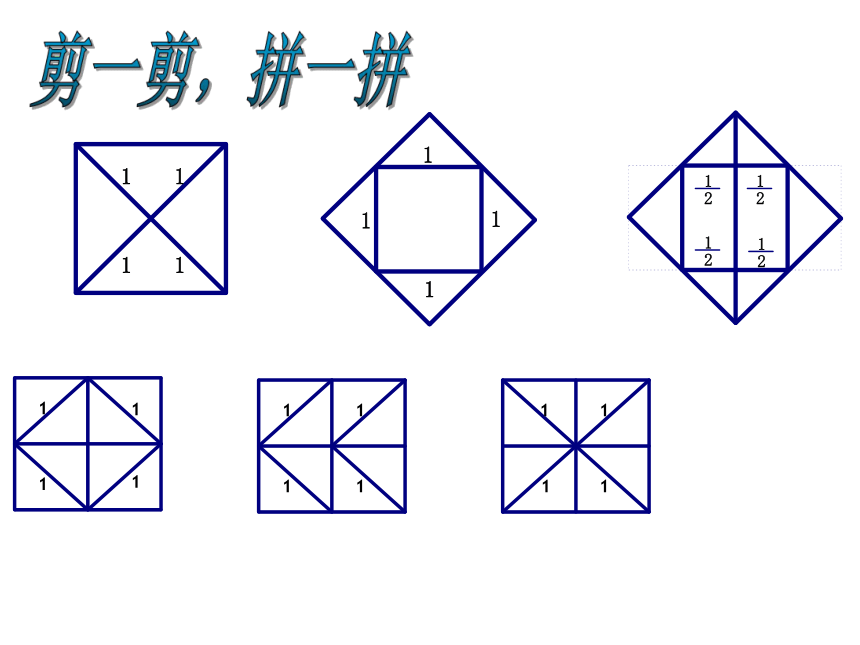
有两个边长为1的小正方形,剪一剪,拼一拼,设法得到一个大的正方形。看看能有几种拼法?
1
1
1
1
完美的正方形
拼图活动
1
1
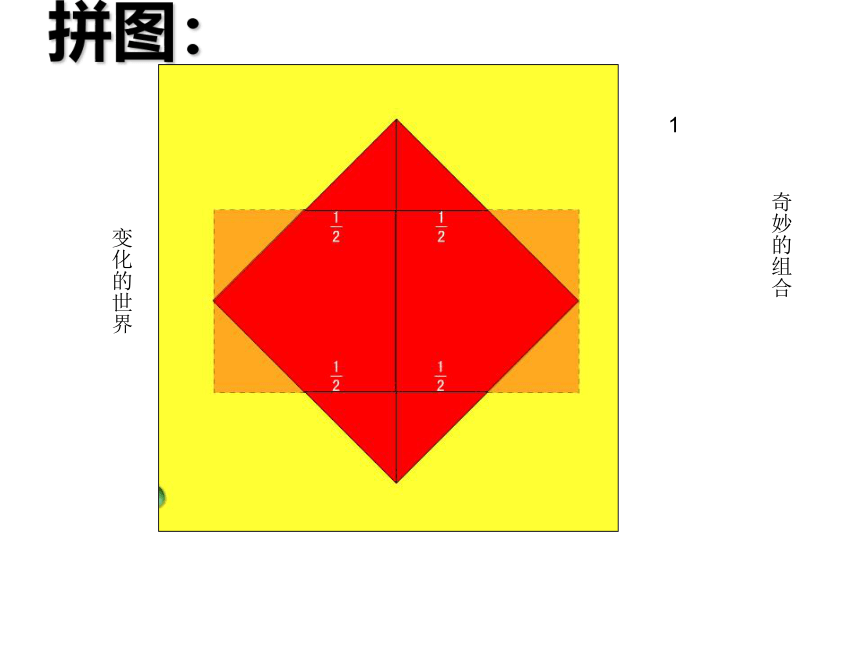
变化的世界
奇妙的组合
拼图:
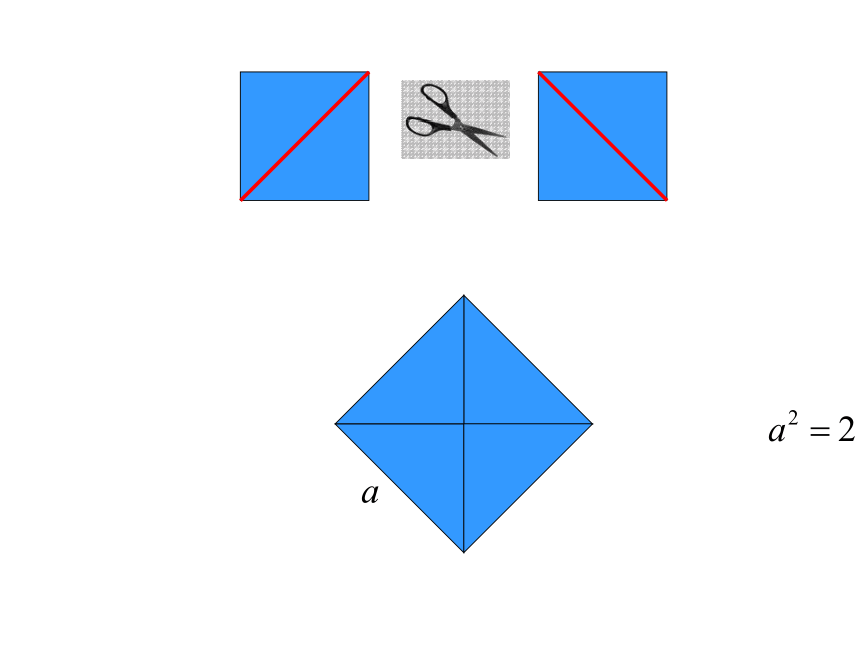
剪一剪,拼一拼
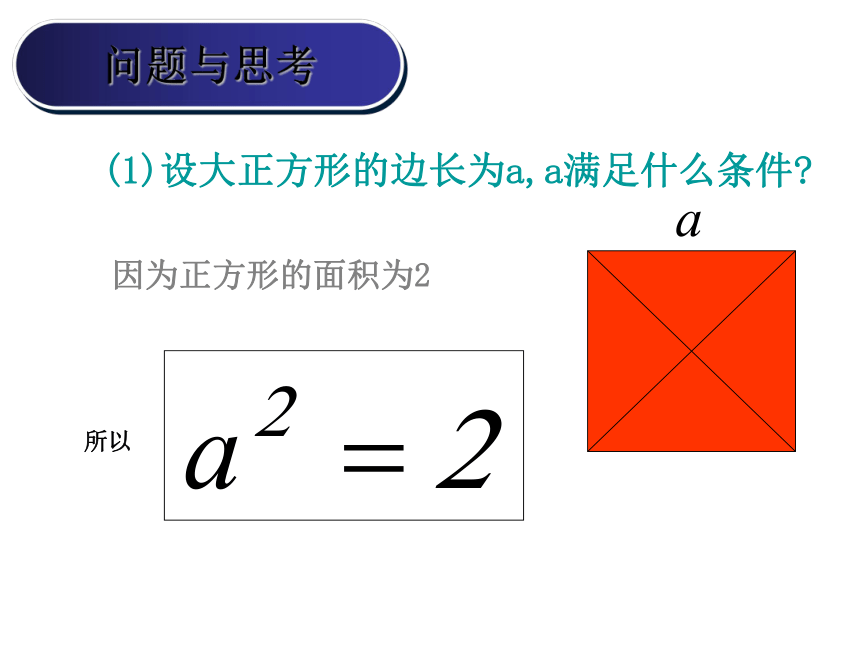
因为正方形的面积为2
所以
(1)设大正方形的边长为a,a满足什么条件?
问题与思考
越来越大,
所以a不可能是整数
a可能是整数吗?
a可能是以2为分母的分数吗?
结果都为分数,所以a不可能是以2为分母的分数。
a可能是以3为分母的分数吗?
结果都为分数,所以a不可能是以3为分母的分数。
a可能是分数吗?
试说出原因。
两个相同的最简分数的乘积仍然是分数,所以a不可能是分数。
a既不是整数又不是分数,所以a一定不是
。
有理数
边长a
面积s
111.41.961.411.98811.4141.9993961.41421.99996164(1)图4-2中,以直角三角形的斜边为边的正方形的面积是多少?
(2)设该正方形的边长为b,b满足什么样条件?
(3)b是有理数吗?
图4-2
1
2
b
???
b2=5
S=5
巧妙的组合
1.如图,正三角形的边长为2,高为h,h可能是整数吗?可能是分数吗?
C
B
A
D
h不可能是整数;
h也不可能是分数。
随堂练习
生活中真的有很多不是有理数的数吗?
1:右图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段。试分别找出两条长度是有理数的线段和两条长度不是有理数的线段。
由勾股定理知:
线段AC,CE,BE的长
不能用有理数表示。
例如:
线段AB,DE,AE的长
能用有理数表示;
思考:
在
中的a,到底是什么样的数呢?
毕达哥拉斯学派认为,宇宙间的一切现象都可用有理数去描述。学派的成员希伯索斯发现有的数不能用有理数来表示,因此他被投入了大海,为真理而献出了宝贵的生命。不是希伯索斯无理,学派这些人的做法才是“无理之举”。人们为了纪念这位为真理献身的学者,把这种数称为
“无理数”。
无理数的发现
数学故事
你能举出其他无理数的例子吗?
无理数的三种形式:
(1)π或含有π的整式
(2)
0.101001000100001·······
(3)
无理数:无限不循环小数
1.无理数是无限不循环小数,有理数是有限小数或
无限循环小数.
2.任何一个有理数都可以化成分数
形式(
p,q
为整数且互质),而无理数不能.
总结:
在数学天地里,重要的不是我们知道什么,而是我们怎么知道——
数学家寄语
毕达哥拉斯
无理数(1)
整数
正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…
分数
正分数:如
,
,5.2,
…
负分数如
,
,-3.5,…
有理数
回顾
&
思考
?
什么叫有理数?
分数与有限小数和无限循环小数可以互化
所以我们把有限小数和无限循环小数都看作分数
回顾
&
思考
?
有理数:整数和分数统称为有理数。
例如:
分数
有限小数
无限循环小数
有两个边长为1的小正方形,剪一剪,拼一拼,设法得到一个大的正方形。看看能有几种拼法?
1
1
1
1
完美的正方形
拼图活动
1
1
变化的世界
奇妙的组合
拼图:
剪一剪,拼一拼
因为正方形的面积为2
所以
(1)设大正方形的边长为a,a满足什么条件?
问题与思考
越来越大,
所以a不可能是整数
a可能是整数吗?
a可能是以2为分母的分数吗?
结果都为分数,所以a不可能是以2为分母的分数。
a可能是以3为分母的分数吗?
结果都为分数,所以a不可能是以3为分母的分数。
a可能是分数吗?
试说出原因。
两个相同的最简分数的乘积仍然是分数,所以a不可能是分数。
a既不是整数又不是分数,所以a一定不是
。
有理数
边长a
面积s
1
(2)设该正方形的边长为b,b满足什么样条件?
(3)b是有理数吗?
图4-2
1
2
b
???
b2=5
S=5
巧妙的组合
1.如图,正三角形的边长为2,高为h,h可能是整数吗?可能是分数吗?
C
B
A
D
h不可能是整数;
h也不可能是分数。
随堂练习
生活中真的有很多不是有理数的数吗?
1:右图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段。试分别找出两条长度是有理数的线段和两条长度不是有理数的线段。
由勾股定理知:
线段AC,CE,BE的长
不能用有理数表示。
例如:
线段AB,DE,AE的长
能用有理数表示;
思考:
在
中的a,到底是什么样的数呢?
毕达哥拉斯学派认为,宇宙间的一切现象都可用有理数去描述。学派的成员希伯索斯发现有的数不能用有理数来表示,因此他被投入了大海,为真理而献出了宝贵的生命。不是希伯索斯无理,学派这些人的做法才是“无理之举”。人们为了纪念这位为真理献身的学者,把这种数称为
“无理数”。
无理数的发现
数学故事
你能举出其他无理数的例子吗?
无理数的三种形式:
(1)π或含有π的整式
(2)
0.101001000100001·······
(3)
无理数:无限不循环小数
1.无理数是无限不循环小数,有理数是有限小数或
无限循环小数.
2.任何一个有理数都可以化成分数
形式(
p,q
为整数且互质),而无理数不能.
总结:
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
