人教版八年级上册 12.2 三角形全等的判定 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版八年级上册 12.2 三角形全等的判定 同步练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 123.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 09:16:53 | ||
图片预览




文档简介
三角形全等的判定
同步练习
一.选择题(共12小题)
1.下列简写的全等三角形的判定定理中,与角没有关系的是( )
A.SSS
B.HL
C.AAS
D.SAS
2.下列条件中,能判定△ABC≌△DEF的是( )
A.∠A=∠D,∠B=∠E,∠C=∠F
B.AB=DE,∠B=∠E,AC=DF
C.∠A=∠D,∠B=∠E,AC=DE
D.AB=DE,∠B=∠E=90°,AC=DF
3.如图,已知△ABC的三条边和三个角,则甲、乙、丙三个三角形中和△ABC全等的是( )
A.甲和乙
B.甲和丙
C.乙和丙
D.只有乙
4.如图,BC∥EF,AC∥DF,添加下列一个条件后,仍无法判断△ABC≌△DEF的是( )
A.BC=EF
B.AC=DF
C.AD=BE
D.∠C=∠F
5.如图,点E,F分别在线段BC上,AB∥CD,AE∥DF,那么添加下列条件还不能判定△ABE≌△DCF的是( )
A.AB=CD
B.∠A=∠D
C.AE=DF
D.CE=BF
6.如图,在△ABC和△DCB中,AC与BD相交于点O,下列四组条件中,不能证明△ABC≌△DCB的是( )
A.AB=DC,AC=DB
B.AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D
D.∠ABD=∠DCA,∠A=∠D
7.如图,D为△ABC边BC上一点,AB=AC,∠BAC=56°,且BF=DC,EC=BD,则∠EDF等于( )
A.62°
B.56°
C.34°
D.124°
8.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③)、④),若要配块与原来大小一样的三角形玻璃,应该带( )
A.第①块
B.第②块
C.第③块
D.第④块
9.如图,点D在线段BC上,若BC=DE,AC=DC,AB=EC,且∠ACE=180°-∠ABC-2x°,则下列角中,大小为x°的角是( )
A.∠EFC
B.∠ABC
C.∠FDC
D.∠DFC
10.如图,线段AB=10,∠A=∠B=45°,AC=BD=4.点E,F为线段AB上两点.从下面4个条件中:
①CE=DF=5;
②AF=BE;
③CE=DF=7;
④∠CEB=∠DFA.
选择一个条件,使得△ACE一定和△BDF全等.则所有满足条件的序号是( )
A.①④
B.②③
C.①②④
D.②③④
11.如图,在△ABC中,高AD和BE交于点H,且∠1=∠2=22.5°,下列结论正确的有( )
①∠1=∠3;②BD+DH=AB;③2AH=BH;④若CD=,则BH=3;⑤若DF⊥BE于点F,则AE-DF=FH.
A.①②④
B.①②⑤
C.②③④
D.③④⑤
12.如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是( )
A.下滑过程中,始终有CC'=DD'
B.下滑过程中,始终有CC'≠DD'
C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'
D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'
二.填空题(共5小题)
13.如图,已知∠ACB=∠DBC,要用“SAS”判断△ABC≌△DCB,需添加的一个条件:
.
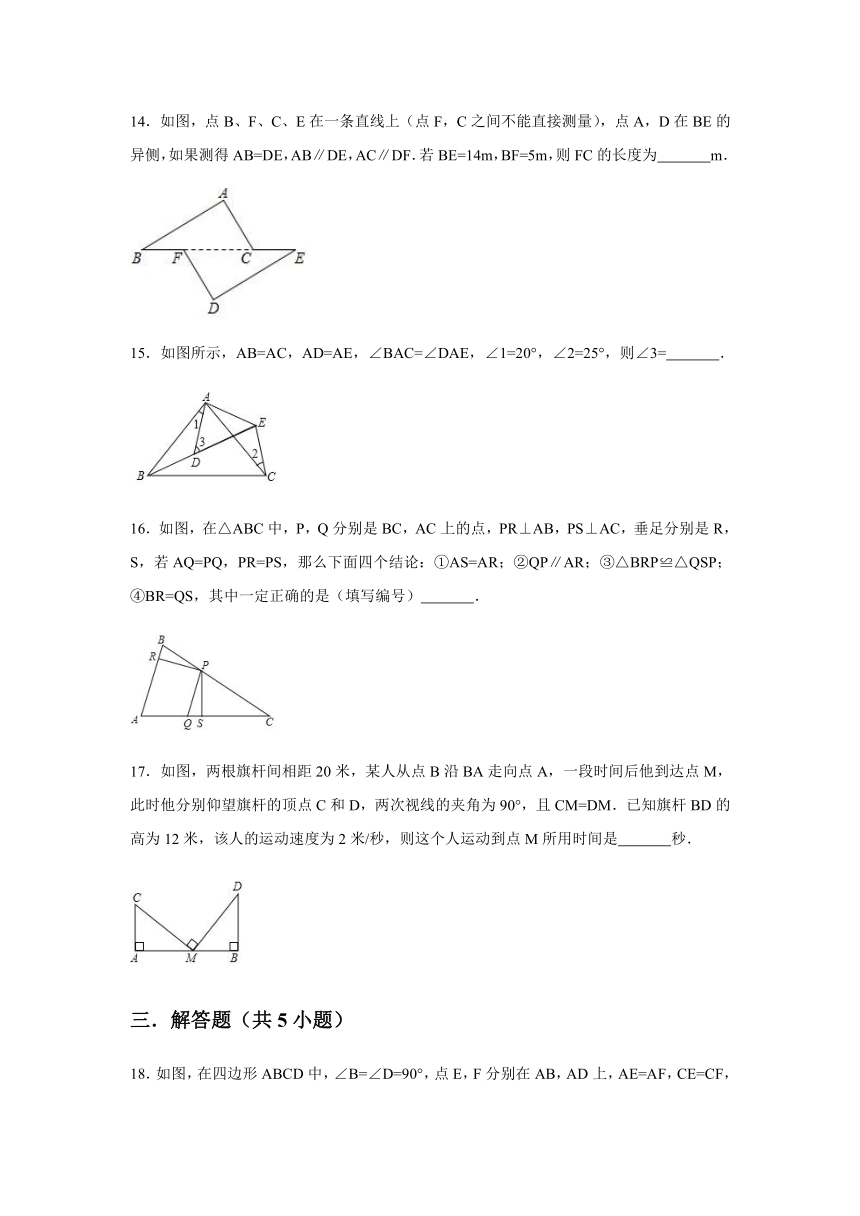
14.如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在BE的异侧,如果测得AB=DE,AB∥DE,AC∥DF.若BE=14m,BF=5m,则FC的长度为
m.
15.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=20°,∠2=25°,则∠3=
.
16.如图,在△ABC中,P,Q分别是BC,AC上的点,PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,那么下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④BR=QS,其中一定正确的是(填写编号)
.
17.如图,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为2米/秒,则这个人运动到点M所用时间是
秒.
三.解答题(共5小题)
18.如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF,求证:CB=CD.
19.如图,在△ABC中,AB=AC,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H,AE=BE.试说明:
(1)△AEH≌△BEC.
(2)AH=2BD.
20.如图,△ABC中,D是BC延长线上一点,满足CD=AB,过点C作CE∥AB且CE=BC,连接DE并延长,分别交AC、AB于点F、G.
(1)求证:△ABC≌△DCE;
(2)若∠B=50°,∠D=22°,求∠AFG的度数.
21.如图,△ABC中,AB=AC,点D在AB边上,点E在AC的延长线上,且CE=BD,连接DE交BC于点F.
(1)求证:EF=DF;
(2)过点D作DG⊥BC,垂足为G,求证:BC=2FG.
22.如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:∠ABE=∠ACE;
(2)如图2,若BE的延长线交AC于点F,CE的延长线交AB于点G.求证:EF=EG.
参考答案
1-5:ADBDB
6-10:DABCD
11-12:BD
AC=BD
4
45°
17、4
18、连接AC,在△AEC与△AFC中
∴△AEC≌△AFC(SSS),
∴∠CAE=∠CAF,
∵∠B=∠D=90°,
∴CB=CD.
19、:(1)∵AD⊥BC,
∴∠DAC+∠C=90°,
∵BE⊥AC,
∴∠EBC+∠C=90°,
∴∠DAC=∠EBC,
在△AEH与△BEC中,
∴△AEH≌△BEC(ASA);
(2)∵△AEH≌△BEC,
∴AH=BC,
∵AB=AC,AD⊥BC,
∴BC=2BD,
∴AH=2BD.
20、(1)证明:∵CE∥AB,
∴∠B=∠DCE,
在△ABC与△DCE中,
∴△ABC≌△DCE(SAS);
(2)解:∵△ABC≌△DCE,∠B=50°,∠D=22°,
∴∠ECD=∠B=50°,∠A=∠D=22°,
∵CE∥AB,
∴∠ACE=∠A=22°,
∵∠CED=180°-∠D-∠ECD=180°-22°-50°=108°,
∴∠AFG=∠DFC=∠CED-∠ACE=108°-22°=86°.
21、证明:(1)过点D作DH∥AC,DH交BC于H,如图1所示:
则∠DHB=∠ACB,∠DHF=∠ECF,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠DHB,
∴BD=HD,
∵CE=BD,
∴HD=CE,
在△DHF和△ECF中,
∴△DHF≌△ECF(AAS),
∴EF=DF;
(2)如图2,由(1)知:BD=HD,
∵DG⊥BC,
∴BG=GH,
由(1)得:△DHF≌△ECF,
∴HF=CF,
∴BC=2FG.
22、:(1)证明:∵点D是BC的中点,
∴BD=CD,
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
在△ABE和△ACE中,
∴△ABE≌△ACE(SAS),
∴∠ABE=∠ACE;
(2)如图,
由(1)知,△ABE≌△ACE,
∴BE=CE,∠ABE=∠ACE,
在△BEG和△CEF中,
∴△BEG≌△CEF(ASA),
∴EG=EF.
同步练习
一.选择题(共12小题)
1.下列简写的全等三角形的判定定理中,与角没有关系的是( )
A.SSS
B.HL
C.AAS
D.SAS
2.下列条件中,能判定△ABC≌△DEF的是( )
A.∠A=∠D,∠B=∠E,∠C=∠F
B.AB=DE,∠B=∠E,AC=DF
C.∠A=∠D,∠B=∠E,AC=DE
D.AB=DE,∠B=∠E=90°,AC=DF
3.如图,已知△ABC的三条边和三个角,则甲、乙、丙三个三角形中和△ABC全等的是( )
A.甲和乙
B.甲和丙
C.乙和丙
D.只有乙
4.如图,BC∥EF,AC∥DF,添加下列一个条件后,仍无法判断△ABC≌△DEF的是( )
A.BC=EF
B.AC=DF
C.AD=BE
D.∠C=∠F
5.如图,点E,F分别在线段BC上,AB∥CD,AE∥DF,那么添加下列条件还不能判定△ABE≌△DCF的是( )
A.AB=CD
B.∠A=∠D
C.AE=DF
D.CE=BF
6.如图,在△ABC和△DCB中,AC与BD相交于点O,下列四组条件中,不能证明△ABC≌△DCB的是( )
A.AB=DC,AC=DB
B.AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D
D.∠ABD=∠DCA,∠A=∠D
7.如图,D为△ABC边BC上一点,AB=AC,∠BAC=56°,且BF=DC,EC=BD,则∠EDF等于( )
A.62°
B.56°
C.34°
D.124°
8.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③)、④),若要配块与原来大小一样的三角形玻璃,应该带( )
A.第①块
B.第②块
C.第③块
D.第④块
9.如图,点D在线段BC上,若BC=DE,AC=DC,AB=EC,且∠ACE=180°-∠ABC-2x°,则下列角中,大小为x°的角是( )
A.∠EFC
B.∠ABC
C.∠FDC
D.∠DFC
10.如图,线段AB=10,∠A=∠B=45°,AC=BD=4.点E,F为线段AB上两点.从下面4个条件中:
①CE=DF=5;
②AF=BE;
③CE=DF=7;
④∠CEB=∠DFA.
选择一个条件,使得△ACE一定和△BDF全等.则所有满足条件的序号是( )
A.①④
B.②③
C.①②④
D.②③④
11.如图,在△ABC中,高AD和BE交于点H,且∠1=∠2=22.5°,下列结论正确的有( )
①∠1=∠3;②BD+DH=AB;③2AH=BH;④若CD=,则BH=3;⑤若DF⊥BE于点F,则AE-DF=FH.
A.①②④
B.①②⑤
C.②③④
D.③④⑤
12.如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是( )
A.下滑过程中,始终有CC'=DD'
B.下滑过程中,始终有CC'≠DD'
C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'
D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'
二.填空题(共5小题)
13.如图,已知∠ACB=∠DBC,要用“SAS”判断△ABC≌△DCB,需添加的一个条件:
.
14.如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在BE的异侧,如果测得AB=DE,AB∥DE,AC∥DF.若BE=14m,BF=5m,则FC的长度为
m.
15.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=20°,∠2=25°,则∠3=
.
16.如图,在△ABC中,P,Q分别是BC,AC上的点,PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,那么下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④BR=QS,其中一定正确的是(填写编号)
.
17.如图,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为2米/秒,则这个人运动到点M所用时间是
秒.
三.解答题(共5小题)
18.如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF,求证:CB=CD.
19.如图,在△ABC中,AB=AC,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H,AE=BE.试说明:
(1)△AEH≌△BEC.
(2)AH=2BD.
20.如图,△ABC中,D是BC延长线上一点,满足CD=AB,过点C作CE∥AB且CE=BC,连接DE并延长,分别交AC、AB于点F、G.
(1)求证:△ABC≌△DCE;
(2)若∠B=50°,∠D=22°,求∠AFG的度数.
21.如图,△ABC中,AB=AC,点D在AB边上,点E在AC的延长线上,且CE=BD,连接DE交BC于点F.
(1)求证:EF=DF;
(2)过点D作DG⊥BC,垂足为G,求证:BC=2FG.
22.如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:∠ABE=∠ACE;
(2)如图2,若BE的延长线交AC于点F,CE的延长线交AB于点G.求证:EF=EG.
参考答案
1-5:ADBDB
6-10:DABCD
11-12:BD
AC=BD
4
45°
17、4
18、连接AC,在△AEC与△AFC中
∴△AEC≌△AFC(SSS),
∴∠CAE=∠CAF,
∵∠B=∠D=90°,
∴CB=CD.
19、:(1)∵AD⊥BC,
∴∠DAC+∠C=90°,
∵BE⊥AC,
∴∠EBC+∠C=90°,
∴∠DAC=∠EBC,
在△AEH与△BEC中,
∴△AEH≌△BEC(ASA);
(2)∵△AEH≌△BEC,
∴AH=BC,
∵AB=AC,AD⊥BC,
∴BC=2BD,
∴AH=2BD.
20、(1)证明:∵CE∥AB,
∴∠B=∠DCE,
在△ABC与△DCE中,
∴△ABC≌△DCE(SAS);
(2)解:∵△ABC≌△DCE,∠B=50°,∠D=22°,
∴∠ECD=∠B=50°,∠A=∠D=22°,
∵CE∥AB,
∴∠ACE=∠A=22°,
∵∠CED=180°-∠D-∠ECD=180°-22°-50°=108°,
∴∠AFG=∠DFC=∠CED-∠ACE=108°-22°=86°.
21、证明:(1)过点D作DH∥AC,DH交BC于H,如图1所示:
则∠DHB=∠ACB,∠DHF=∠ECF,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠DHB,
∴BD=HD,
∵CE=BD,
∴HD=CE,
在△DHF和△ECF中,
∴△DHF≌△ECF(AAS),
∴EF=DF;
(2)如图2,由(1)知:BD=HD,
∵DG⊥BC,
∴BG=GH,
由(1)得:△DHF≌△ECF,
∴HF=CF,
∴BC=2FG.
22、:(1)证明:∵点D是BC的中点,
∴BD=CD,
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
在△ABE和△ACE中,
∴△ABE≌△ACE(SAS),
∴∠ABE=∠ACE;
(2)如图,
由(1)知,△ABE≌△ACE,
∴BE=CE,∠ABE=∠ACE,
在△BEG和△CEF中,
∴△BEG≌△CEF(ASA),
∴EG=EF.
