人教版八年级上册 11.3 多边形及其内角和 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版八年级上册 11.3 多边形及其内角和 同步练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 151.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 09:15:37 | ||
图片预览


文档简介
多边形及其内角和
同步练习
一.选择题(共12小题)
1.多边形的内角和不可能为( )
A.180°
B.540°
C.1080°
D.1200°
2.一个n边形的每一个外角都是72°,则n等于( )
A.3
B.4
C.5
D.6
3.若某多边形的边数增加1,则这个多边形的外角和( )
A.增加180°
B.增加360°
C.减少180°
D.不变
4.一个多边形的外角和是内角和的七分之二,这个多边形的边数是( )
A.7
B.8
C.9
D.10
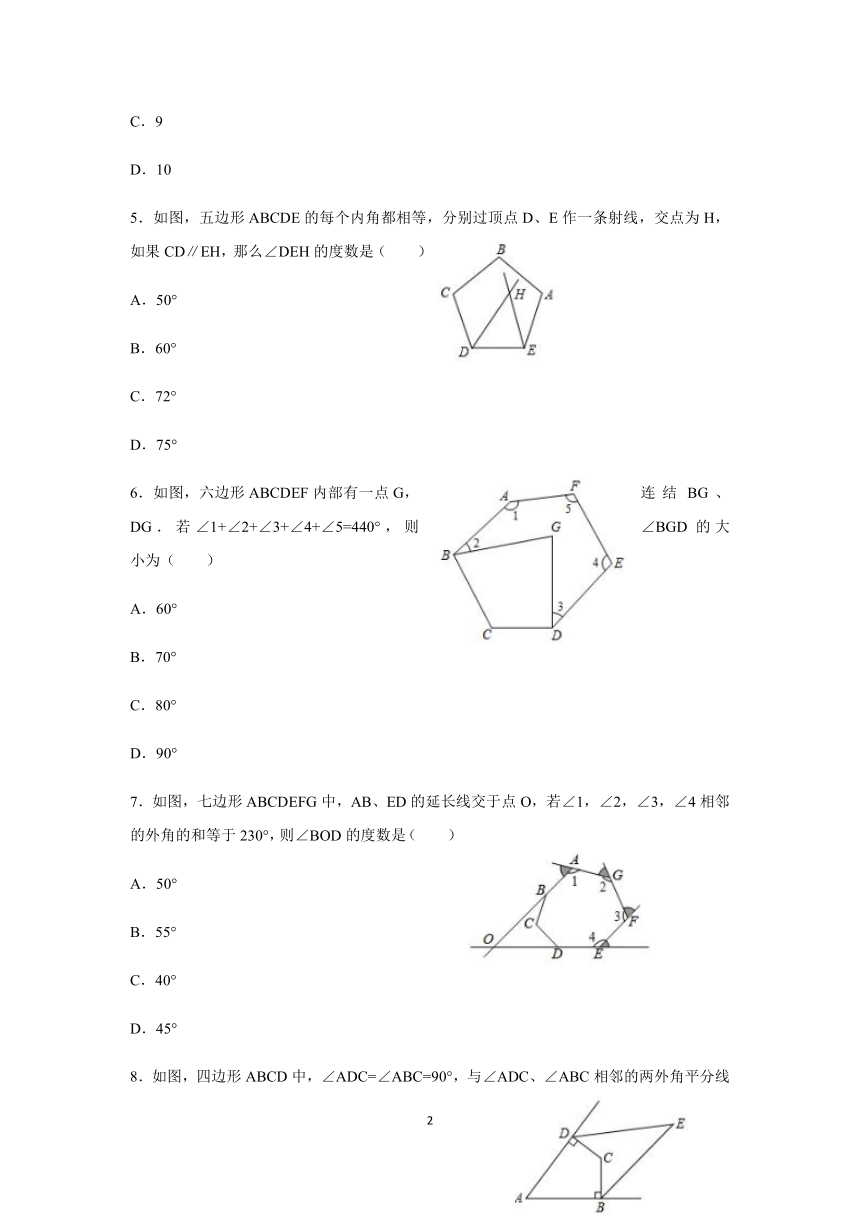
5.如图,五边形ABCDE的每个内角都相等,分别过顶点D、E作一条射线,交点为H,如果CD∥EH,那么∠DEH的度数是( )
A.50°
B.60°
C.72°
D.75°
6.如图,六边形ABCDEF内部有一点G,连结BG、DG.若∠1+∠2+∠3+∠4+∠5=440°,则∠BGD的大小为( )
A.60°
B.70°
C.80°
D.90°
7.如图,七边形ABCDEFG中,AB、ED的延长线交于点O,若∠1,∠2,∠3,∠4相邻的外角的和等于230°,则∠BOD的度数是( )
A.50°
B.55°
C.40°
D.45°
8.如图,四边形ABCD中,∠ADC=∠ABC=90°,与∠ADC、∠ABC相邻的两外角平分线交于点E,若∠A=60°,则∠E的度数为( )
A.60°
B.50°
C.40°
D.30°
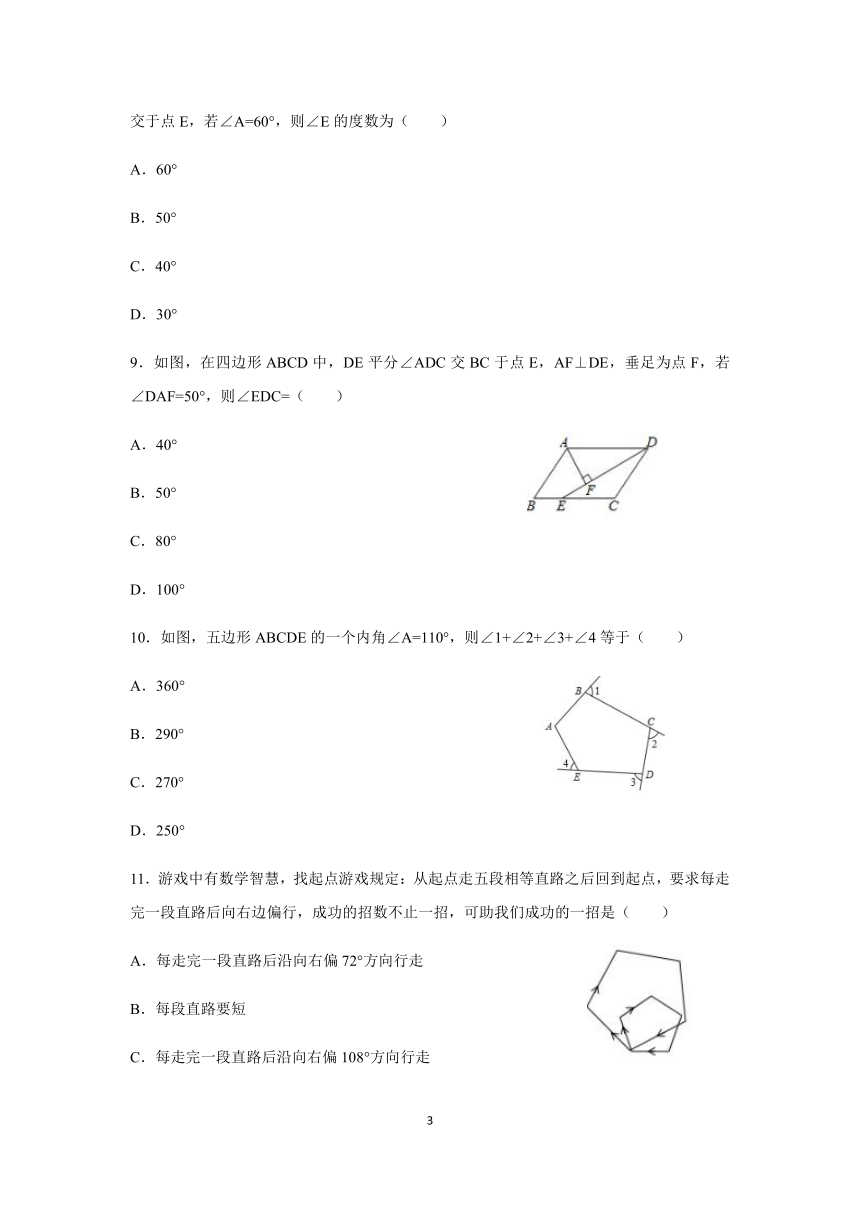
9.如图,在四边形ABCD中,DE平分∠ADC交BC于点E,AF⊥DE,垂足为点F,若∠DAF=50°,则∠EDC=( )
A.40°
B.50°
C.80°
D.100°
10.如图,五边形ABCDE的一个内角∠A=110°,则∠1+∠2+∠3+∠4等于( )
A.360°
B.290°
C.270°
D.250°
11.游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行,成功的招数不止一招,可助我们成功的一招是( )
A.每走完一段直路后沿向右偏72°方向行走
B.每段直路要短
C.每走完一段直路后沿向右偏108°方向行走
D.每段直路要长
12.如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D…照这样走下去,小明第一次回到出发点A时所走的路程为( )
A.100米
B.80米
C.60米
D.40米
二.填空题(共5小题)
13.如果一个多边形的每个内角为160°,那么它的边数为
.
14.如图,在一个三角形的纸片(△ABC)中,∠C=90°,将这个纸片沿直线DE剪去一个角后变成一个四边形ABED,则图中∠1+∠2的度数为
°.
15.四边形具有不稳定性.如图,矩形ABCD按箭头方向变形成平行四边形A'B'C'D',变形后∠A'=30°,若矩形ABCD的面积是9,则平行四边形A'B'C'D'的面积是
16.如图,四边形ABCD中,且∠1,∠2分别是∠BCD和∠BAD的邻补角,则∠1+∠2=150°.则∠B+∠ADC=
.
17.如图,在七边形ABCDEFG中,AB、ED的延长线交于点O,若∠1、∠2、∠3、∠4的外角和等于225°,则∠BOD=
°.
三.解答题(共4小题)
18.如图,∠DEA=90°,∠MDE=100°,∠GBC=65°,∠DCH=50°,求∠EAB的度数.
19.如图,在五边形ABCDE中,∠A=∠B、∠BCD=∠DEA,并且∠CED=∠ECD,你能判定AB与EC平行吗?为什么?
20.四边形的边比三角形的边多了一条,内角和多了多少度?五边形的边比四边形的边多了一条,内角和多了多少度?由此可以推测,多边形的边每多一条,内角和多了多少度?说明你的理由.
21.如图,下列四边形是同一个四边形不断缩小(保持形状不变)的结果.
(1)在图中标出各个四边形的外角;
(2)在缩小的过程中,四边形对应的各个外角的大小是否发生了变化?
(3)如果保持四边形的形状不变,将四边形不断缩小下去,你能想象一下最终的形状吗?你能借助上面的变化过程说明四边形的外角和吗?
(4)你能类似地说明五边形、六边形……一般多边形的外角和吗?
参考答案
1-5:DCDCC
6-10:CADAB
11-12:AB
13、18
14、270
15、4.5
16、150
17、45
18、:∵∠DEA=90°,
∴∠AEN=90°,
又∵∠EAF+∠AEN+∠MDE+∠GBC+∠DCH=∠EAF+90°+100°+65°+50°=360°,
∴∠EAF=55°,
又∵∠EAB+∠EAF=180°,
∴∠EAB=180°-∠EAF=125°.
19、:∵∠BCD=∠DEA,∠CED=∠ECD,
∴∠CEA=∠ECB,
∵∠A=∠B,
∴由四边形内角和为360°可得∠CEA+∠A=180°,
∴AB∥EC.
20、四边形的边比三角形的边多了一条,内角和多了360°-180°=180°,五边形的边比四边形的边多了一条,内角和多了540°-360°=180°,由此可以推测,多边形的边每多一条,内角和多了180°,
∵多边形的内角和为:(n-2)×180°,
∴若多边形边数每多一条,则它的内角和多了(n+1-2)×180°-(n-2)×180°=180°.
21、:(1)如图所示:
(2)在缩小的过程中,四边形对应的各个外角的大小不变;
(3)如果保持四边形的形状不变,将四边形不断缩小下去,最终的形状是一个点,所以四边形的外角拼凑为一个周角.
∵四边形的内角和为:(4-2)×180°=360°,
∠1+∠BAD+∠2+∠ABC+∠3+∠BCD+∠4+∠CDA=4×180°=720°,
∴∠1+∠2+∠3+∠4=720°-(∠BAD+∠ABC+∠BCD+∠CDA)=720°-360°=360°,
即四边形的外角和为360°.
(4)如图所示:
∵五边形的内角和为:(5-2)×180°=540°,
∠1+∠BAE+∠2+∠ABC+∠3+∠BCD+∠4+∠CDE+∠5+∠DEA=5×180°=900°,
∴∠1+∠2+∠3+∠4+∠5=900°-(∠BAE+∠ABC+∠BCD+∠CDE+∠DEA)=900°-540°=360°,
即五边形的外角和为360°.
类似地,五边形、六边形……一般多边形的外角和等于360°.
同步练习
一.选择题(共12小题)
1.多边形的内角和不可能为( )
A.180°
B.540°
C.1080°
D.1200°
2.一个n边形的每一个外角都是72°,则n等于( )
A.3
B.4
C.5
D.6
3.若某多边形的边数增加1,则这个多边形的外角和( )
A.增加180°
B.增加360°
C.减少180°
D.不变
4.一个多边形的外角和是内角和的七分之二,这个多边形的边数是( )
A.7
B.8
C.9
D.10
5.如图,五边形ABCDE的每个内角都相等,分别过顶点D、E作一条射线,交点为H,如果CD∥EH,那么∠DEH的度数是( )
A.50°
B.60°
C.72°
D.75°
6.如图,六边形ABCDEF内部有一点G,连结BG、DG.若∠1+∠2+∠3+∠4+∠5=440°,则∠BGD的大小为( )
A.60°
B.70°
C.80°
D.90°
7.如图,七边形ABCDEFG中,AB、ED的延长线交于点O,若∠1,∠2,∠3,∠4相邻的外角的和等于230°,则∠BOD的度数是( )
A.50°
B.55°
C.40°
D.45°
8.如图,四边形ABCD中,∠ADC=∠ABC=90°,与∠ADC、∠ABC相邻的两外角平分线交于点E,若∠A=60°,则∠E的度数为( )
A.60°
B.50°
C.40°
D.30°
9.如图,在四边形ABCD中,DE平分∠ADC交BC于点E,AF⊥DE,垂足为点F,若∠DAF=50°,则∠EDC=( )
A.40°
B.50°
C.80°
D.100°
10.如图,五边形ABCDE的一个内角∠A=110°,则∠1+∠2+∠3+∠4等于( )
A.360°
B.290°
C.270°
D.250°
11.游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行,成功的招数不止一招,可助我们成功的一招是( )
A.每走完一段直路后沿向右偏72°方向行走
B.每段直路要短
C.每走完一段直路后沿向右偏108°方向行走
D.每段直路要长
12.如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D…照这样走下去,小明第一次回到出发点A时所走的路程为( )
A.100米
B.80米
C.60米
D.40米
二.填空题(共5小题)
13.如果一个多边形的每个内角为160°,那么它的边数为
.
14.如图,在一个三角形的纸片(△ABC)中,∠C=90°,将这个纸片沿直线DE剪去一个角后变成一个四边形ABED,则图中∠1+∠2的度数为
°.
15.四边形具有不稳定性.如图,矩形ABCD按箭头方向变形成平行四边形A'B'C'D',变形后∠A'=30°,若矩形ABCD的面积是9,则平行四边形A'B'C'D'的面积是
16.如图,四边形ABCD中,且∠1,∠2分别是∠BCD和∠BAD的邻补角,则∠1+∠2=150°.则∠B+∠ADC=
.
17.如图,在七边形ABCDEFG中,AB、ED的延长线交于点O,若∠1、∠2、∠3、∠4的外角和等于225°,则∠BOD=
°.
三.解答题(共4小题)
18.如图,∠DEA=90°,∠MDE=100°,∠GBC=65°,∠DCH=50°,求∠EAB的度数.
19.如图,在五边形ABCDE中,∠A=∠B、∠BCD=∠DEA,并且∠CED=∠ECD,你能判定AB与EC平行吗?为什么?
20.四边形的边比三角形的边多了一条,内角和多了多少度?五边形的边比四边形的边多了一条,内角和多了多少度?由此可以推测,多边形的边每多一条,内角和多了多少度?说明你的理由.
21.如图,下列四边形是同一个四边形不断缩小(保持形状不变)的结果.
(1)在图中标出各个四边形的外角;
(2)在缩小的过程中,四边形对应的各个外角的大小是否发生了变化?
(3)如果保持四边形的形状不变,将四边形不断缩小下去,你能想象一下最终的形状吗?你能借助上面的变化过程说明四边形的外角和吗?
(4)你能类似地说明五边形、六边形……一般多边形的外角和吗?
参考答案
1-5:DCDCC
6-10:CADAB
11-12:AB
13、18
14、270
15、4.5
16、150
17、45
18、:∵∠DEA=90°,
∴∠AEN=90°,
又∵∠EAF+∠AEN+∠MDE+∠GBC+∠DCH=∠EAF+90°+100°+65°+50°=360°,
∴∠EAF=55°,
又∵∠EAB+∠EAF=180°,
∴∠EAB=180°-∠EAF=125°.
19、:∵∠BCD=∠DEA,∠CED=∠ECD,
∴∠CEA=∠ECB,
∵∠A=∠B,
∴由四边形内角和为360°可得∠CEA+∠A=180°,
∴AB∥EC.
20、四边形的边比三角形的边多了一条,内角和多了360°-180°=180°,五边形的边比四边形的边多了一条,内角和多了540°-360°=180°,由此可以推测,多边形的边每多一条,内角和多了180°,
∵多边形的内角和为:(n-2)×180°,
∴若多边形边数每多一条,则它的内角和多了(n+1-2)×180°-(n-2)×180°=180°.
21、:(1)如图所示:
(2)在缩小的过程中,四边形对应的各个外角的大小不变;
(3)如果保持四边形的形状不变,将四边形不断缩小下去,最终的形状是一个点,所以四边形的外角拼凑为一个周角.
∵四边形的内角和为:(4-2)×180°=360°,
∠1+∠BAD+∠2+∠ABC+∠3+∠BCD+∠4+∠CDA=4×180°=720°,
∴∠1+∠2+∠3+∠4=720°-(∠BAD+∠ABC+∠BCD+∠CDA)=720°-360°=360°,
即四边形的外角和为360°.
(4)如图所示:
∵五边形的内角和为:(5-2)×180°=540°,
∠1+∠BAE+∠2+∠ABC+∠3+∠BCD+∠4+∠CDE+∠5+∠DEA=5×180°=900°,
∴∠1+∠2+∠3+∠4+∠5=900°-(∠BAE+∠ABC+∠BCD+∠CDE+∠DEA)=900°-540°=360°,
即五边形的外角和为360°.
类似地,五边形、六边形……一般多边形的外角和等于360°.
