人教版九年级上册 数学 课件: 24.2.2直线和圆的位置关系(共19张PPT)
文档属性
| 名称 | 人教版九年级上册 数学 课件: 24.2.2直线和圆的位置关系(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 197.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 09:11:18 | ||
图片预览



文档简介
(共19张PPT)
直线和圆的位置关系
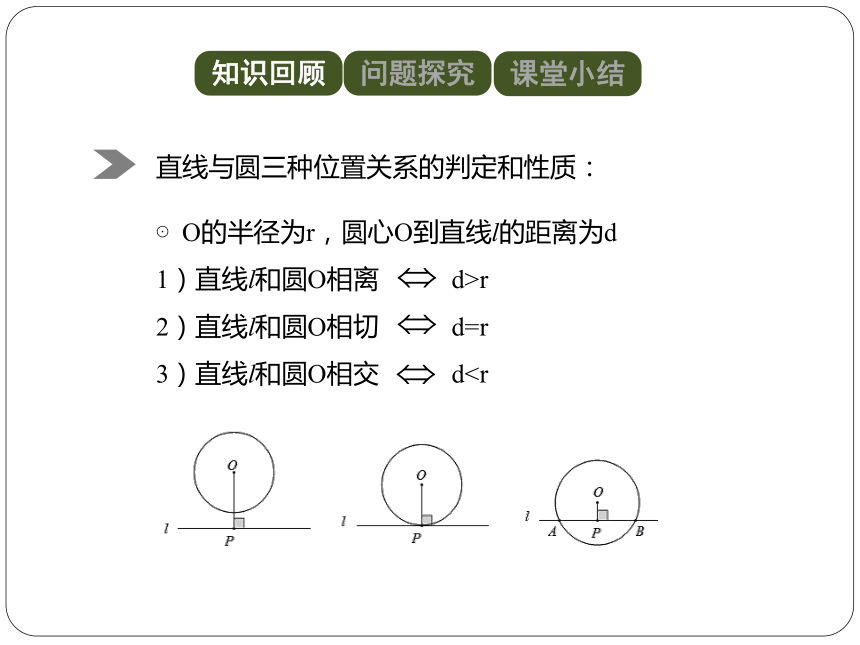
⊙O的半径为r,圆心O到直线l的距离为d
1)直线l和圆O相离
d>r
2)直线l和圆O相切
d=r
3)直线l和圆O相交
d直线与圆三种位置关系的判定和性质:
知识回顾
问题探究
课堂小结
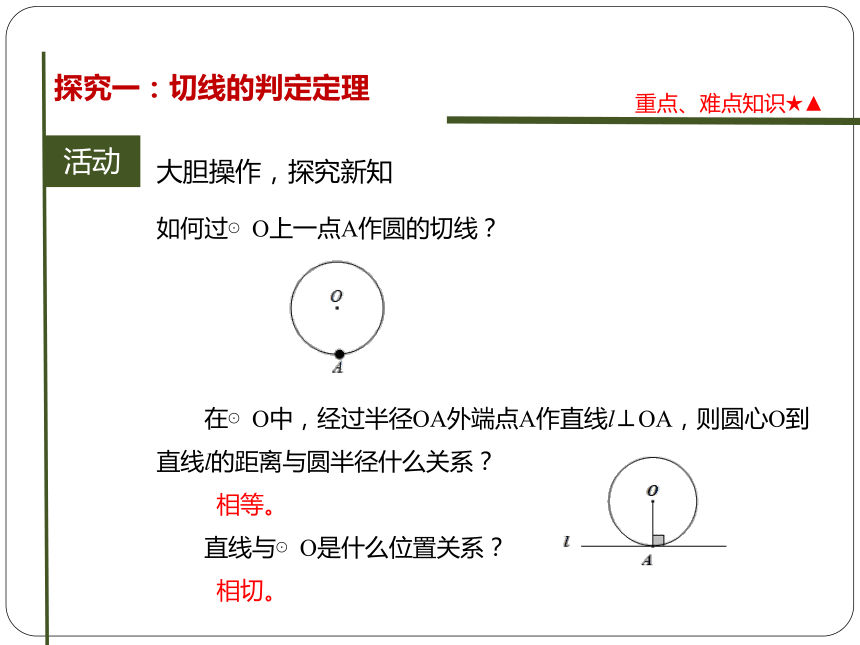
如何过⊙O上一点A作圆的切线?
在⊙O中,经过半径OA外端点A作直线l⊥OA,则圆心O到直线l的距离与圆半径什么关系?
相等。
直线与⊙O是什么位置关系?
相切。
探究一:切线的判定定理
活动
大胆操作,探究新知
重点、难点知识★▲
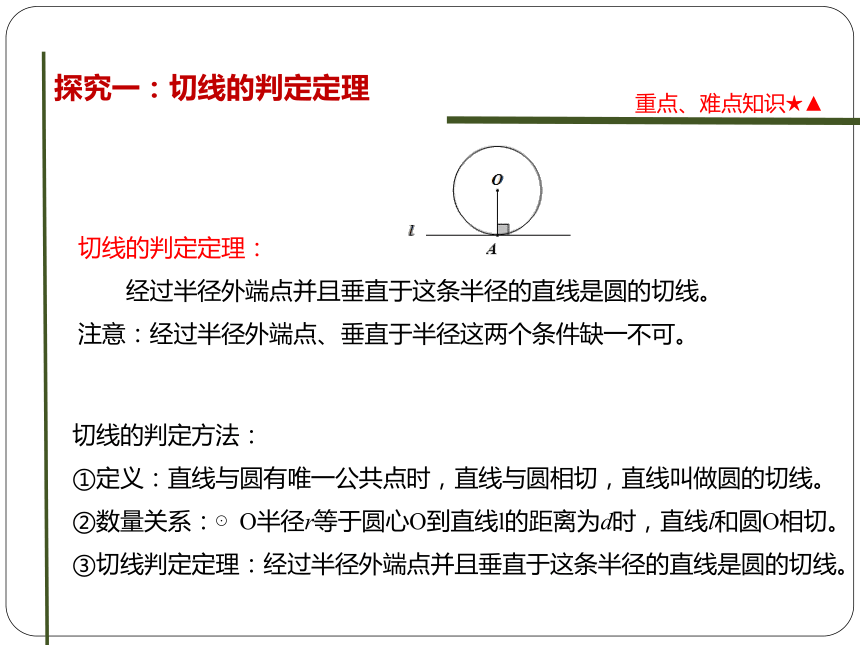
切线的判定定理:
经过半径外端点并且垂直于这条半径的直线是圆的切线。
注意:经过半径外端点、垂直于半径这两个条件缺一不可。
切线的判定方法:
①定义:直线与圆有唯一公共点时,直线与圆相切,直线叫做圆的切线。
②数量关系:⊙O半径r等于圆心O到直线l的距离为d时,直线l和圆O相切。③切线判定定理:经过半径外端点并且垂直于这条半径的直线是圆的切线。
探究一:切线的判定定理
重点、难点知识★▲
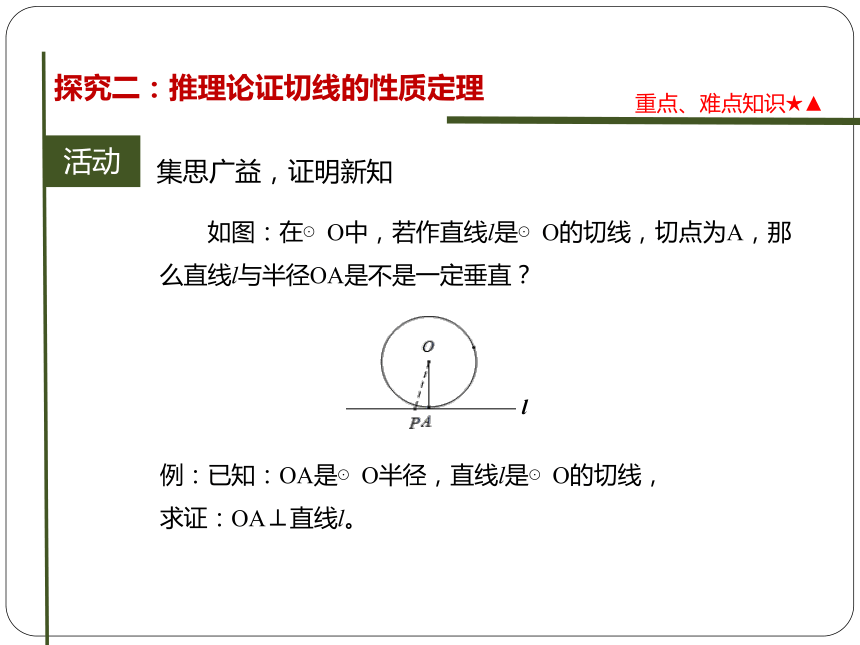
如图:在⊙O中,若作直线l是⊙O的切线,切点为A,那么直线l与半径OA是不是一定垂直?
探究二:推理论证切线的性质定理
活动
集思广益,证明新知
重点、难点知识★▲
例:已知:OA是⊙O半径,直线l是⊙O的切线,
求证:OA⊥直线l。
l
证明:(反证法)
假设OA⊥直线l不成立,过点O作OP⊥直线l于点P,
∴OA为Rt△OPA的斜边。
又∵OP⊥l于P,
∴OP的长就是圆心O到切线l的距离,
∴OP的长等于⊙O的半径,即OA=OP,
这与“直角三角形的斜边大于直角边”矛盾。
所以假设OA与l不垂直不成立。
例:已知:OA是⊙O半径,直线l是⊙O的切线,
求证:OA⊥直线l。
l
切线性质:圆的切线垂直于经过切点的半径。
探究二:推理论证切线的性质定理
重点、难点知识★▲
例1.下列命题中,假命题是( )。
A.经过半径的端点且垂直于这条半径的直线是圆的切线
B.经过直径的端点且垂直于这条直径的直线是圆的切线
C.经过圆心且垂直于切线的直线必经过切点
D.经过切点且垂直于切线的直线必经过圆心
解:根据切线的判定定理:经过半径的外端点且垂直于这条半径的直线是圆的切线。故A选项是假命题。
探究三:切线的判定定理和性质定理的应用
活动1
基础性例题
重点、难点知识★▲
A
练习:下列说法正确的是(
)。
A.经过半径外端的直线是圆的切线
B.若射线与圆有一个交点,则射线是圆的切线
C.垂直于半径的直线是圆的切线
D.圆的切线垂直于经过切点的半径
解:根据切线的判定定理:经过半径的外端点且垂直于这条半径的直线是圆的切线。故A选项是错误的。
射线与圆有一个交点但不一定垂直于过该点的半径,所以B选项错误。垂直于半径且经过半径外端点的直线是圆的切线,故C选项错误。
D
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
例2.AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连接BC,若∠P=40°,则∠B等于( )。
A.20°
B.25°
C.30°
D.40°
【思路点拨】
由切线的性质得:切线垂直于过切点的半径∠PAB=90°,根据直角三角形的两锐角互余计算∠POA=50°,最后利用同圆的半径相等得等腰三角形进行计算。
活动2
提升型例题
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
例2.
AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连接BC,若∠P=40°,则∠B等于( )。
A.20°
B.25°
C.30°
D.40°
解:∵PA切⊙O于点A,
∴∠PAB=90°,
∵∠P=40°,
∴∠POA=90°-40°=50°,
∵OC=OB,
∴∠B=∠BCO=25°。
B
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
练习:如图,△ABC的边AC经过圆心O,且与⊙O相交于C,D两点,边AB与⊙O相切,切点为B。如果∠A=34°,那么∠C等于( )。
A.28°
B.33°
C.34°
D.56°
【思路点拨】运用切线的性质来进行计算或论证,常用辅助线:连接圆心和切点,得直角三角形,再根据直角相关性质求解。
A
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
解:如图,连结OB,
∵AB与⊙O相切,
∴OB⊥AB,∠ABO=90°,
∴∠AOB=90°﹣∠A=90°﹣34°=56°,
∵∠AOB=∠C+∠OBC,
∴∠C+∠OBC=56°,
而OB=OC,
∴∠C=∠OBC,
∴∠C=
×56°=28°。
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
例3.如图:已知△ABC中,AB=AC,O是底边BC的中点,AB与⊙O相切于点D,猜测AC与⊙O有怎样的位置关系?
【思路点拨】切线判定方法的常规辅助线:未知切点,作垂线段,证垂线段与半径相等。
活动3
探究型例题
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
解:AC是⊙O的切线,理由如下:
证明:如图过点O作OE⊥AC于点E,连结OD,OA
∵AB与⊙O相切于点D,
∴AB⊥OD,
∵AB=AC,O是底边BC的中点,
∴AO是∠BAC的平分线,
∴OE=OD,OE是⊙O的半径,
∵AC经过⊙O的半径OE的外端点且垂直于OE,
∴AC是⊙O的切线。
例3.
如图:已知△ABC中,AB=AC,O是底边BC的中点,AB与⊙O相切于点D,猜测AC与⊙O有怎样的位置关系?
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
练习:已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
【思路点拨】已知切点,连半径,运用等腰三角形性质证垂直。
解:连接OC
∵OA=OB,CA=CB
∴OC⊥AB
∵直线AB经过⊙O上的点C
∴直线AB是⊙O的切线
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
(1)切线的判定定理:经过半径外端点并且垂直于这条半径的直线是圆的切线。
(2)切线的判定方法:(归纳总结)
①定义:直线与圆有唯一公共点时,直线与圆相切,直线叫做圆的切线。
②切线判断定理:经过半径外端点并且垂直于这条半径的直线是圆的切线。
(3)切线性质:圆的切线垂直于经过切点的半径。
③数量关系:⊙O的半径为r,圆心O到直线l的距离为d,若d=r,则直线l
和圆O相切。
(1)已知切线时常常把切点与圆心相连,利用切线性质解题。
(2)切线的判定常规辅助线:
切点未知,作垂线段,证垂线段与半径等;
切点已知,连半径,证垂直。
谢
谢
直线和圆的位置关系
⊙O的半径为r,圆心O到直线l的距离为d
1)直线l和圆O相离
d>r
2)直线l和圆O相切
d=r
3)直线l和圆O相交
d
知识回顾
问题探究
课堂小结
如何过⊙O上一点A作圆的切线?
在⊙O中,经过半径OA外端点A作直线l⊥OA,则圆心O到直线l的距离与圆半径什么关系?
相等。
直线与⊙O是什么位置关系?
相切。
探究一:切线的判定定理
活动
大胆操作,探究新知
重点、难点知识★▲
切线的判定定理:
经过半径外端点并且垂直于这条半径的直线是圆的切线。
注意:经过半径外端点、垂直于半径这两个条件缺一不可。
切线的判定方法:
①定义:直线与圆有唯一公共点时,直线与圆相切,直线叫做圆的切线。
②数量关系:⊙O半径r等于圆心O到直线l的距离为d时,直线l和圆O相切。③切线判定定理:经过半径外端点并且垂直于这条半径的直线是圆的切线。
探究一:切线的判定定理
重点、难点知识★▲
如图:在⊙O中,若作直线l是⊙O的切线,切点为A,那么直线l与半径OA是不是一定垂直?
探究二:推理论证切线的性质定理
活动
集思广益,证明新知
重点、难点知识★▲
例:已知:OA是⊙O半径,直线l是⊙O的切线,
求证:OA⊥直线l。
l
证明:(反证法)
假设OA⊥直线l不成立,过点O作OP⊥直线l于点P,
∴OA为Rt△OPA的斜边。
又∵OP⊥l于P,
∴OP的长就是圆心O到切线l的距离,
∴OP的长等于⊙O的半径,即OA=OP,
这与“直角三角形的斜边大于直角边”矛盾。
所以假设OA与l不垂直不成立。
例:已知:OA是⊙O半径,直线l是⊙O的切线,
求证:OA⊥直线l。
l
切线性质:圆的切线垂直于经过切点的半径。
探究二:推理论证切线的性质定理
重点、难点知识★▲
例1.下列命题中,假命题是( )。
A.经过半径的端点且垂直于这条半径的直线是圆的切线
B.经过直径的端点且垂直于这条直径的直线是圆的切线
C.经过圆心且垂直于切线的直线必经过切点
D.经过切点且垂直于切线的直线必经过圆心
解:根据切线的判定定理:经过半径的外端点且垂直于这条半径的直线是圆的切线。故A选项是假命题。
探究三:切线的判定定理和性质定理的应用
活动1
基础性例题
重点、难点知识★▲
A
练习:下列说法正确的是(
)。
A.经过半径外端的直线是圆的切线
B.若射线与圆有一个交点,则射线是圆的切线
C.垂直于半径的直线是圆的切线
D.圆的切线垂直于经过切点的半径
解:根据切线的判定定理:经过半径的外端点且垂直于这条半径的直线是圆的切线。故A选项是错误的。
射线与圆有一个交点但不一定垂直于过该点的半径,所以B选项错误。垂直于半径且经过半径外端点的直线是圆的切线,故C选项错误。
D
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
例2.AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连接BC,若∠P=40°,则∠B等于( )。
A.20°
B.25°
C.30°
D.40°
【思路点拨】
由切线的性质得:切线垂直于过切点的半径∠PAB=90°,根据直角三角形的两锐角互余计算∠POA=50°,最后利用同圆的半径相等得等腰三角形进行计算。
活动2
提升型例题
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
例2.
AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连接BC,若∠P=40°,则∠B等于( )。
A.20°
B.25°
C.30°
D.40°
解:∵PA切⊙O于点A,
∴∠PAB=90°,
∵∠P=40°,
∴∠POA=90°-40°=50°,
∵OC=OB,
∴∠B=∠BCO=25°。
B
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
练习:如图,△ABC的边AC经过圆心O,且与⊙O相交于C,D两点,边AB与⊙O相切,切点为B。如果∠A=34°,那么∠C等于( )。
A.28°
B.33°
C.34°
D.56°
【思路点拨】运用切线的性质来进行计算或论证,常用辅助线:连接圆心和切点,得直角三角形,再根据直角相关性质求解。
A
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
解:如图,连结OB,
∵AB与⊙O相切,
∴OB⊥AB,∠ABO=90°,
∴∠AOB=90°﹣∠A=90°﹣34°=56°,
∵∠AOB=∠C+∠OBC,
∴∠C+∠OBC=56°,
而OB=OC,
∴∠C=∠OBC,
∴∠C=
×56°=28°。
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
例3.如图:已知△ABC中,AB=AC,O是底边BC的中点,AB与⊙O相切于点D,猜测AC与⊙O有怎样的位置关系?
【思路点拨】切线判定方法的常规辅助线:未知切点,作垂线段,证垂线段与半径相等。
活动3
探究型例题
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
解:AC是⊙O的切线,理由如下:
证明:如图过点O作OE⊥AC于点E,连结OD,OA
∵AB与⊙O相切于点D,
∴AB⊥OD,
∵AB=AC,O是底边BC的中点,
∴AO是∠BAC的平分线,
∴OE=OD,OE是⊙O的半径,
∵AC经过⊙O的半径OE的外端点且垂直于OE,
∴AC是⊙O的切线。
例3.
如图:已知△ABC中,AB=AC,O是底边BC的中点,AB与⊙O相切于点D,猜测AC与⊙O有怎样的位置关系?
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
练习:已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
【思路点拨】已知切点,连半径,运用等腰三角形性质证垂直。
解:连接OC
∵OA=OB,CA=CB
∴OC⊥AB
∵直线AB经过⊙O上的点C
∴直线AB是⊙O的切线
重点、难点知识★▲
探究三:切线的判定定理和性质定理的应用
(1)切线的判定定理:经过半径外端点并且垂直于这条半径的直线是圆的切线。
(2)切线的判定方法:(归纳总结)
①定义:直线与圆有唯一公共点时,直线与圆相切,直线叫做圆的切线。
②切线判断定理:经过半径外端点并且垂直于这条半径的直线是圆的切线。
(3)切线性质:圆的切线垂直于经过切点的半径。
③数量关系:⊙O的半径为r,圆心O到直线l的距离为d,若d=r,则直线l
和圆O相切。
(1)已知切线时常常把切点与圆心相连,利用切线性质解题。
(2)切线的判定常规辅助线:
切点未知,作垂线段,证垂线段与半径等;
切点已知,连半径,证垂直。
谢
谢
同课章节目录
