数学:同步授课课件 13.3.1《实数1》(人教实验版八年级上)
文档属性
| 名称 | 数学:同步授课课件 13.3.1《实数1》(人教实验版八年级上) |  | |
| 格式 | zip | ||
| 文件大小 | 657.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-23 12:33:52 | ||
图片预览




文档简介
(共19张PPT)
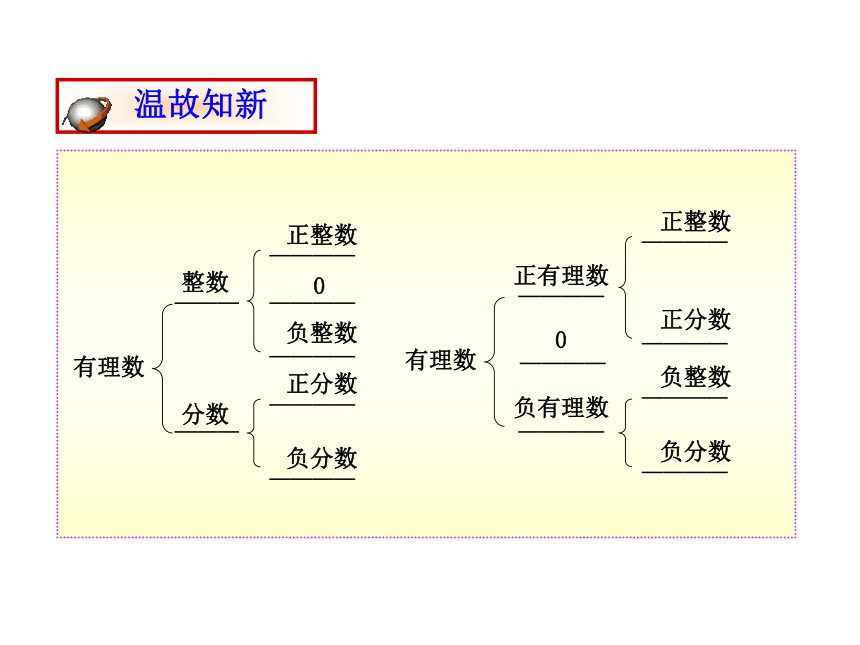
温故知新
————
有理数
整数
分数
正整数
负整数
0
正分数
负分数
有理数
正有理数
负有理数
正整数
正分数
0
负整数
负分数
———
———
————
————
————
————
————
————
————
————
————
————
————
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
探究发现
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
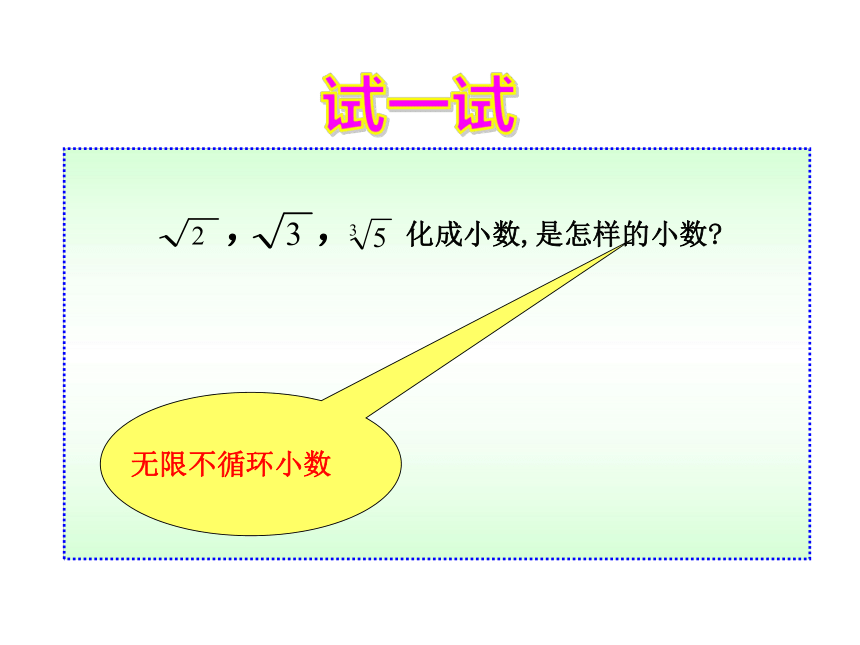
, , 化成小数,是怎样的小数
无限不循环小数
无限不循环的小数 ---------- 叫做无理数.
你能举出一些无理数吗?
0.1010010001…〔两个1之间依次多1个0〕
—168.3232232223…〔两个3之间依次多1个2〕
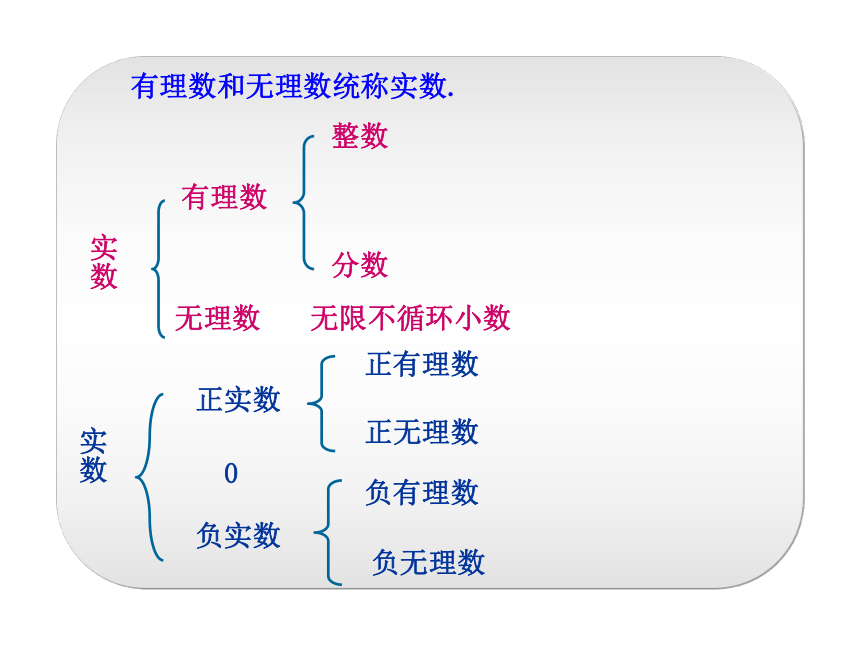
有理数和无理数统称实数.
实数
实数
有理数
无理数
整数
分数
无限不循环小数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
1.圆周率 及一些含有 的数
2.开不尽方的数
3.有一定的规律,但不循环的无限小数
无理数的特征:
注意:带根号的数不一定是无理数
总结技巧
快
乐
套
餐
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
×
×
整数有
有理数有
无理数有
实数有
二、填空
在实数
中,
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
无理数的相反数、倒数、绝对值的意义是什么呢?
练一练
填空
2、 的相反数是 ,绝对值是 .
3、绝对值等于 的数是 , 的平方是 .
1、正实数的绝对值是 ,0的绝对值是 ,负实数的绝对值是 .
它本身
0
它的相反数
每个有理数都可以用数轴上的点表示,那么无理数
是否也可以用数轴上的点来表示呢?
想一想:
你能在数轴上找到表示 这样的无
理数的点吗?
0
1
2
4
3
-1
-2
π
直径为1的圆
0
1
2
4
3
-1
-2
问题:边长为1的正方形,对角线长为多少
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
实数与数轴上的点是一一对应的.
谈谈收获
1. 无限不循环的小数叫做无理数.
2.有理数和无理数统称实数.
3.在实数范围内,相反数、倒数、绝对值的意义
和有理数范围内的相反数、倒数、绝对值的意
义完全一样。
4.实数与数轴上的点是一一对应的.
温故知新
————
有理数
整数
分数
正整数
负整数
0
正分数
负分数
有理数
正有理数
负有理数
正整数
正分数
0
负整数
负分数
———
———
————
————
————
————
————
————
————
————
————
————
————
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
探究发现
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
, , 化成小数,是怎样的小数
无限不循环小数
无限不循环的小数 ---------- 叫做无理数.
你能举出一些无理数吗?
0.1010010001…〔两个1之间依次多1个0〕
—168.3232232223…〔两个3之间依次多1个2〕
有理数和无理数统称实数.
实数
实数
有理数
无理数
整数
分数
无限不循环小数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
1.圆周率 及一些含有 的数
2.开不尽方的数
3.有一定的规律,但不循环的无限小数
无理数的特征:
注意:带根号的数不一定是无理数
总结技巧
快
乐
套
餐
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
×
×
整数有
有理数有
无理数有
实数有
二、填空
在实数
中,
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
无理数的相反数、倒数、绝对值的意义是什么呢?
练一练
填空
2、 的相反数是 ,绝对值是 .
3、绝对值等于 的数是 , 的平方是 .
1、正实数的绝对值是 ,0的绝对值是 ,负实数的绝对值是 .
它本身
0
它的相反数
每个有理数都可以用数轴上的点表示,那么无理数
是否也可以用数轴上的点来表示呢?
想一想:
你能在数轴上找到表示 这样的无
理数的点吗?
0
1
2
4
3
-1
-2
π
直径为1的圆
0
1
2
4
3
-1
-2
问题:边长为1的正方形,对角线长为多少
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
实数与数轴上的点是一一对应的.
谈谈收获
1. 无限不循环的小数叫做无理数.
2.有理数和无理数统称实数.
3.在实数范围内,相反数、倒数、绝对值的意义
和有理数范围内的相反数、倒数、绝对值的意
义完全一样。
4.实数与数轴上的点是一一对应的.
