人教版数学八年级上册12.1全等三角形 课件(共22张PPT)
文档属性
| 名称 | 人教版数学八年级上册12.1全等三角形 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
全等三角形
思考:同一张底片洗出的两张照片
叠放在一起怎么样?
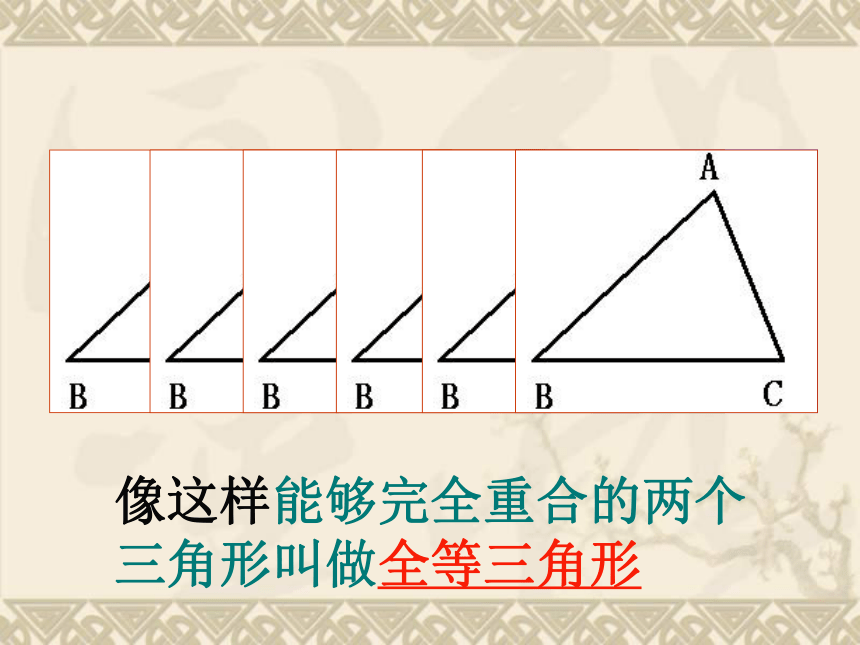
能够完全重合的两个图形叫做全等形
全等形的形状、大小相同
观察:在上面的图形中哪两个图形叠放在一起能够完全重合?
像这样能够完全重合的两个三角形叫做全等三角形
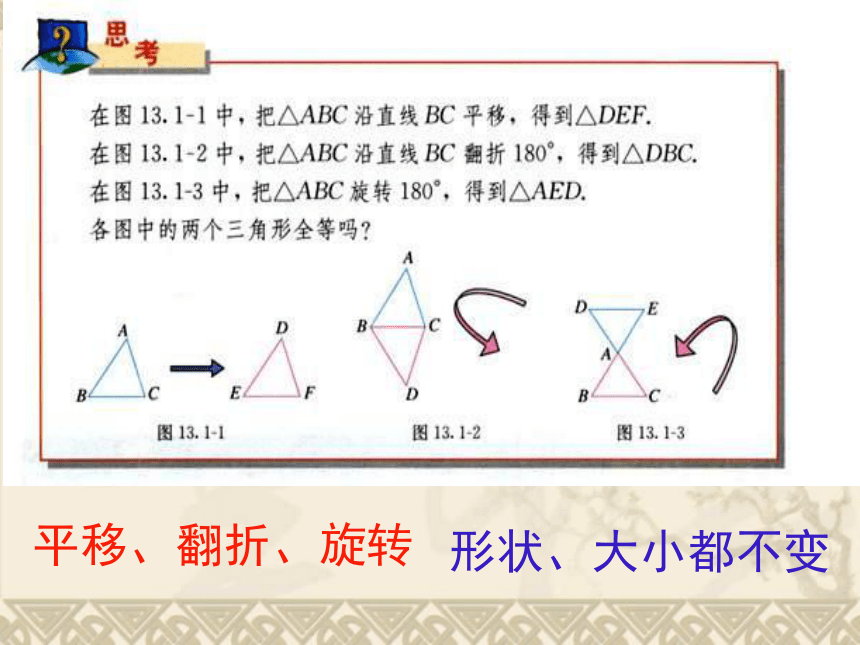
平移、翻折、旋转
形状、大小都不变
A
B
C
D
E
F
看一看
看一看
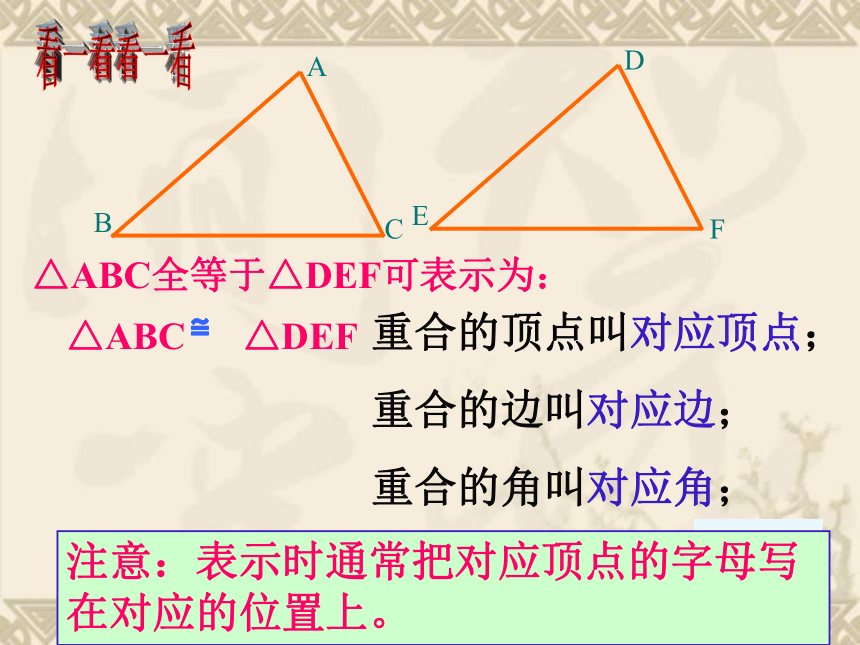
△ABC全等于△DEF可表示为:
△ABC
△DEF
注意:表示时通常把对应顶点的字母写在对应的位置上。
≌
重合的顶点叫对应顶点;
重合的边叫对应边;
重合的角叫对应角;
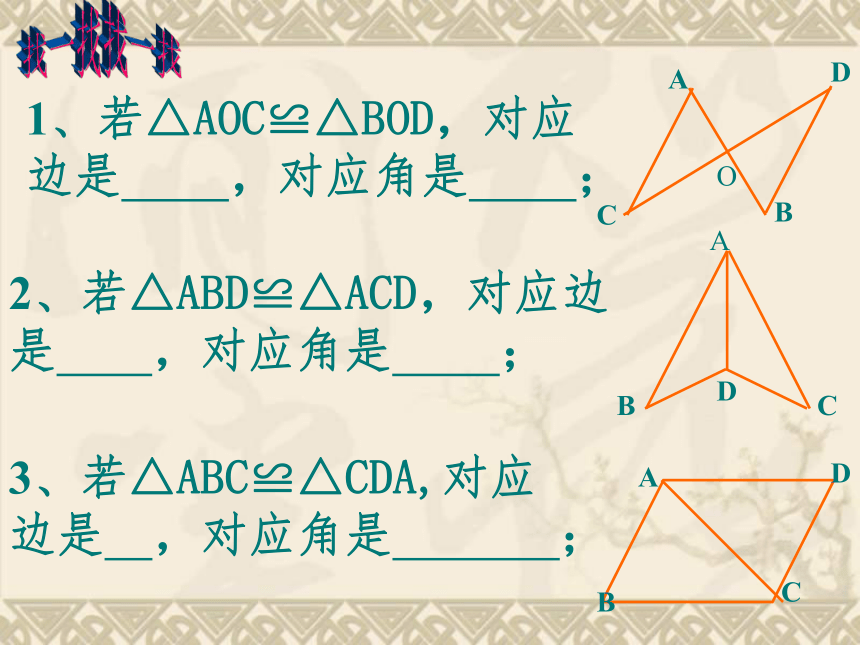
1、若△AOC≌△BOD,对应
边是
,对应角是
;
A
B
O
C
D
2、若△ABD≌△ACD,对应边是
,对应角是
;
A
B
C
D
3、若△ABC≌△CDA,对应
边是
,对应角是
;
A
B
C
D
找一找
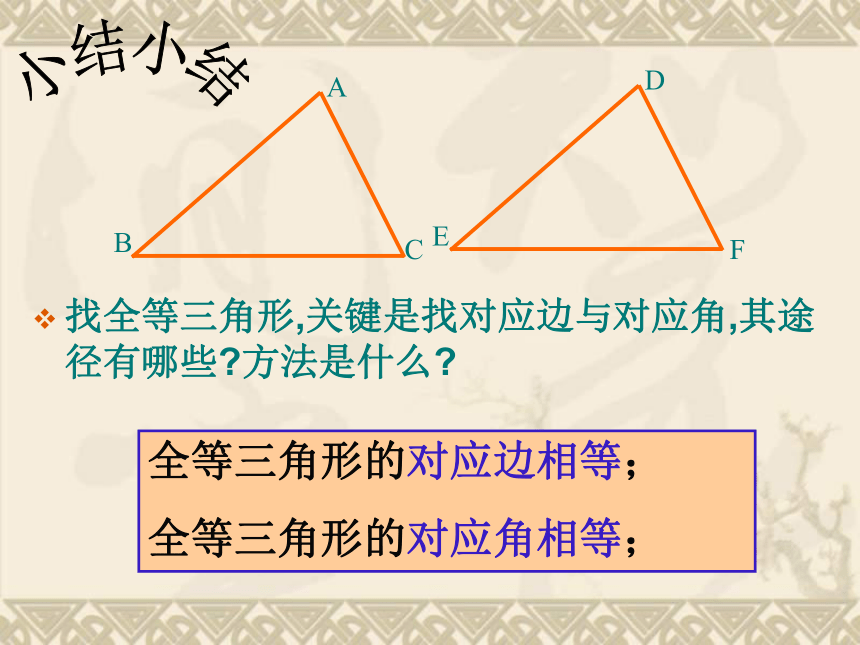
找全等三角形,关键是找对应边与对应角,其途径有哪些?方法是什么?
小结
A
B
C
D
E
F
全等三角形的对应边相等;
全等三角形的对应角相等;
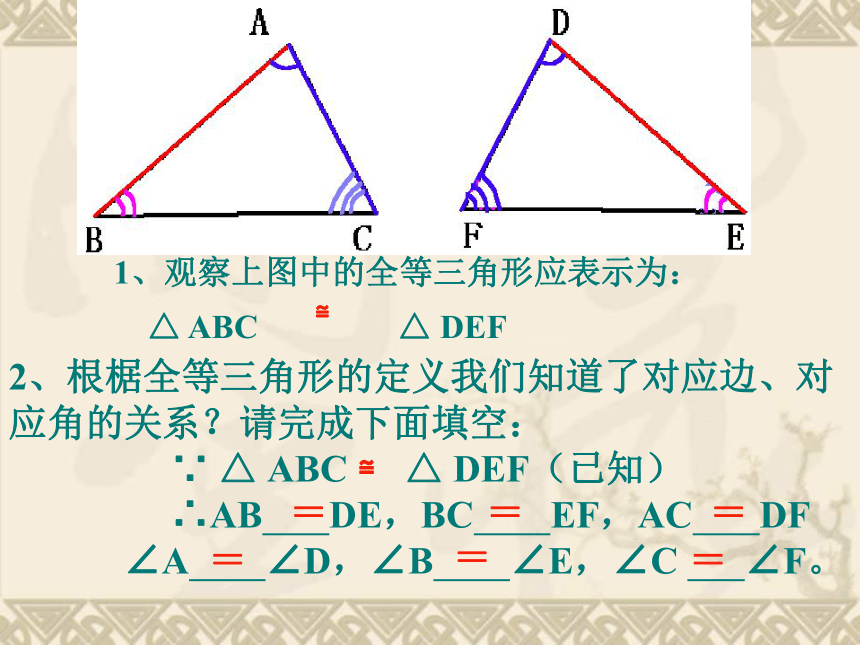
1、观察上图中的全等三角形应表示为:
≌
2、根椐全等三角形的定义我们知道了对应边、对应角的关系?请完成下面填空:
∵
△
ABC
≌
△
DEF(已知)
∴AB
DE,BC
EF,AC
DF
∠A
∠D,∠B
∠E,∠C
∠F。
△
ABC
△
DEF
=
=
=
=
=
=
如图,已知△ABC≌△ADE,
∠C=∠E,BC=DE,其它的对应边
有
:_____________
对应角有:_____________
A
B
C
D
E
找一找
全等三角形的符号表示:
“≌”
读作:全等于
如图:
△ABC≌△DEF
∵
∴A
B=D
E,A
C=D
F,B
C=EF(全等三角形对应边相等)
全等三角形的性质:对应边相等,对应角相等
∠A=∠D,∠B=∠E,∠C=∠F(全等三角形的对应角相等)
强调:在表示全等三角形边、角相等时对应顶点写在对应位置上
如图,△ABD≌△ACE,若∠B=25°,BD=6㎝,AD=4㎝,你能得出△ACE中哪些角的大小,哪些边的长度吗?为什么
?
A
B
C
D
E
求一求
O
2、已知△ABC≌△DEF,A与D、B与E分别是对应顶点,∠
A=52°,∠B=67°,BC
=15㎝。
则∠F=________
,EF=______㎝。
求一求
练习1
ΔABC≌ΔDEF,AB=DE,AC=DF,BC=EF.写出所有对应角相等的式子。
C
D
F
A
E
B
答:∠A=∠EDF,
∠B=∠E,
∠BCA=∠EFD
练习
1、如图:
△ABC≌△DCB
其中的对应边: 与 ; 与 ; 与 。
对应角: 与 ; 与 ; 与 。
A
D
B
C
已知ΔABC≌ΔADE,
∠B=∠D,∠C=∠E,∠BAC=∠DAE。写出对应边相等的式子
B
E
A
C
D
答:AC=AE
AB=AD
BC=DE
右图是一个等边三角形,你能把它分成两个全等的三角形吗?你能把它分成三个、四个全等的三角形吗?
议一议
1、能够
的两个图形叫做全等图形。两个三角形重合时,互相
的顶点叫做对应顶点。记两个全等三角形时,通常把表示
顶点的字母写在
的位置上。
A
B
C
D
E
2、如图△ABC≌
△ADE若∠D=
∠B,
∠C=
∠AED,则∠DAE=
;
∠DAB=
。
练一练
3、如图△
ABD
≌
△CDB,若AB=4,AD=5,BD=6,则BC=
,CD=
。
4、如图△ABD≌
△EBC,AB=3cm,BC=5cm,求DE的长.
4、如图,Rt△ABD和Rt
△EBC中,BA=BE,BD=BC,则△ABD经过怎样的运动就可以与
△EBC重合?并指出相等的线段与相等的角。
如图,已知△
AOC
≌
△BOD
求证:AC∥BD
能力提高
A
B
C
D
E
如图所示,在△ABC中,D、E分别是边AC、BC上的点,若△EAB
≌
△EDB
≌
△EDC,则∠C的度数是(
)0
(A)15
(B)20
(C)25
(D)30
全等三角形
思考:同一张底片洗出的两张照片
叠放在一起怎么样?
能够完全重合的两个图形叫做全等形
全等形的形状、大小相同
观察:在上面的图形中哪两个图形叠放在一起能够完全重合?
像这样能够完全重合的两个三角形叫做全等三角形
平移、翻折、旋转
形状、大小都不变
A
B
C
D
E
F
看一看
看一看
△ABC全等于△DEF可表示为:
△ABC
△DEF
注意:表示时通常把对应顶点的字母写在对应的位置上。
≌
重合的顶点叫对应顶点;
重合的边叫对应边;
重合的角叫对应角;
1、若△AOC≌△BOD,对应
边是
,对应角是
;
A
B
O
C
D
2、若△ABD≌△ACD,对应边是
,对应角是
;
A
B
C
D
3、若△ABC≌△CDA,对应
边是
,对应角是
;
A
B
C
D
找一找
找全等三角形,关键是找对应边与对应角,其途径有哪些?方法是什么?
小结
A
B
C
D
E
F
全等三角形的对应边相等;
全等三角形的对应角相等;
1、观察上图中的全等三角形应表示为:
≌
2、根椐全等三角形的定义我们知道了对应边、对应角的关系?请完成下面填空:
∵
△
ABC
≌
△
DEF(已知)
∴AB
DE,BC
EF,AC
DF
∠A
∠D,∠B
∠E,∠C
∠F。
△
ABC
△
DEF
=
=
=
=
=
=
如图,已知△ABC≌△ADE,
∠C=∠E,BC=DE,其它的对应边
有
:_____________
对应角有:_____________
A
B
C
D
E
找一找
全等三角形的符号表示:
“≌”
读作:全等于
如图:
△ABC≌△DEF
∵
∴A
B=D
E,A
C=D
F,B
C=EF(全等三角形对应边相等)
全等三角形的性质:对应边相等,对应角相等
∠A=∠D,∠B=∠E,∠C=∠F(全等三角形的对应角相等)
强调:在表示全等三角形边、角相等时对应顶点写在对应位置上
如图,△ABD≌△ACE,若∠B=25°,BD=6㎝,AD=4㎝,你能得出△ACE中哪些角的大小,哪些边的长度吗?为什么
?
A
B
C
D
E
求一求
O
2、已知△ABC≌△DEF,A与D、B与E分别是对应顶点,∠
A=52°,∠B=67°,BC
=15㎝。
则∠F=________
,EF=______㎝。
求一求
练习1
ΔABC≌ΔDEF,AB=DE,AC=DF,BC=EF.写出所有对应角相等的式子。
C
D
F
A
E
B
答:∠A=∠EDF,
∠B=∠E,
∠BCA=∠EFD
练习
1、如图:
△ABC≌△DCB
其中的对应边: 与 ; 与 ; 与 。
对应角: 与 ; 与 ; 与 。
A
D
B
C
已知ΔABC≌ΔADE,
∠B=∠D,∠C=∠E,∠BAC=∠DAE。写出对应边相等的式子
B
E
A
C
D
答:AC=AE
AB=AD
BC=DE
右图是一个等边三角形,你能把它分成两个全等的三角形吗?你能把它分成三个、四个全等的三角形吗?
议一议
1、能够
的两个图形叫做全等图形。两个三角形重合时,互相
的顶点叫做对应顶点。记两个全等三角形时,通常把表示
顶点的字母写在
的位置上。
A
B
C
D
E
2、如图△ABC≌
△ADE若∠D=
∠B,
∠C=
∠AED,则∠DAE=
;
∠DAB=
。
练一练
3、如图△
ABD
≌
△CDB,若AB=4,AD=5,BD=6,则BC=
,CD=
。
4、如图△ABD≌
△EBC,AB=3cm,BC=5cm,求DE的长.
4、如图,Rt△ABD和Rt
△EBC中,BA=BE,BD=BC,则△ABD经过怎样的运动就可以与
△EBC重合?并指出相等的线段与相等的角。
如图,已知△
AOC
≌
△BOD
求证:AC∥BD
能力提高
A
B
C
D
E
如图所示,在△ABC中,D、E分别是边AC、BC上的点,若△EAB
≌
△EDB
≌
△EDC,则∠C的度数是(
)0
(A)15
(B)20
(C)25
(D)30
