人教版数学八年级上册12.2.5三角形全等的判定-HL 课件(共22张PPT)
文档属性
| 名称 | 人教版数学八年级上册12.2.5三角形全等的判定-HL 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 261.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 08:52:02 | ||
图片预览

文档简介
(共22张PPT)
探索三角形全等的条件
(HL)
忆一忆
1、全等三角形的对应边
---------,
对应角-----------
相等
相等
2、判定三角形全等的方法有:
SAS、ASA、AAS、SSS
直角边
直角边
斜边
3、认识直角三角形
Rt△ABC
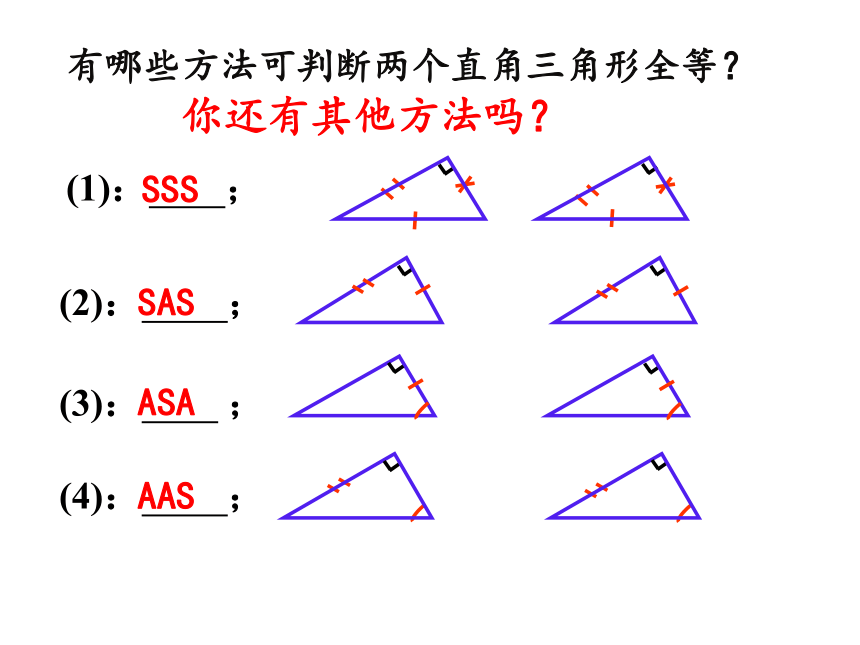
有哪些方法可判断两个直角三角形全等?
(1):
;
(2):
;
(3):
;
(4):
;
SSS
SAS
ASA
AAS
你还有其他方法吗?
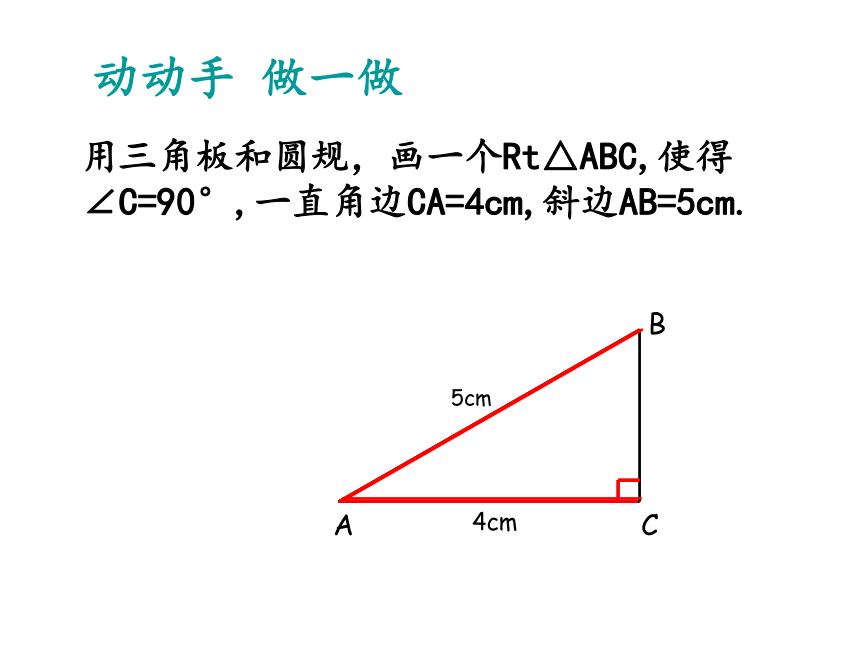
动动手
做一做
用三角板和圆规,画一个Rt△ABC,使得∠C=90°,一直角边CA=4cm,斜边AB=5cm.
A
B
C
5cm
4cm
动动手
做一做
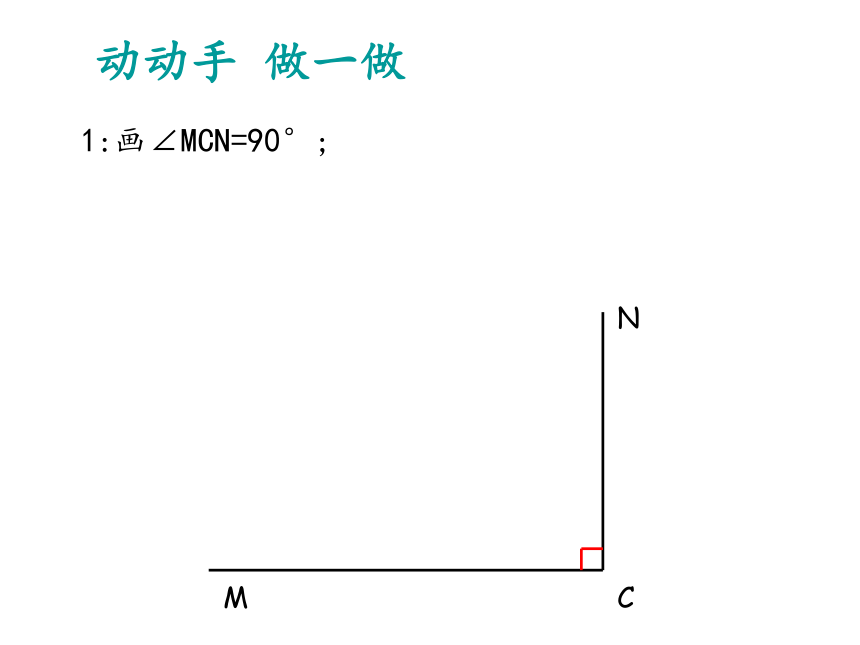
1:画∠MCN=90°;
C
N
M
动动手
做一做
1:画∠MCN=90°;
C
N
M
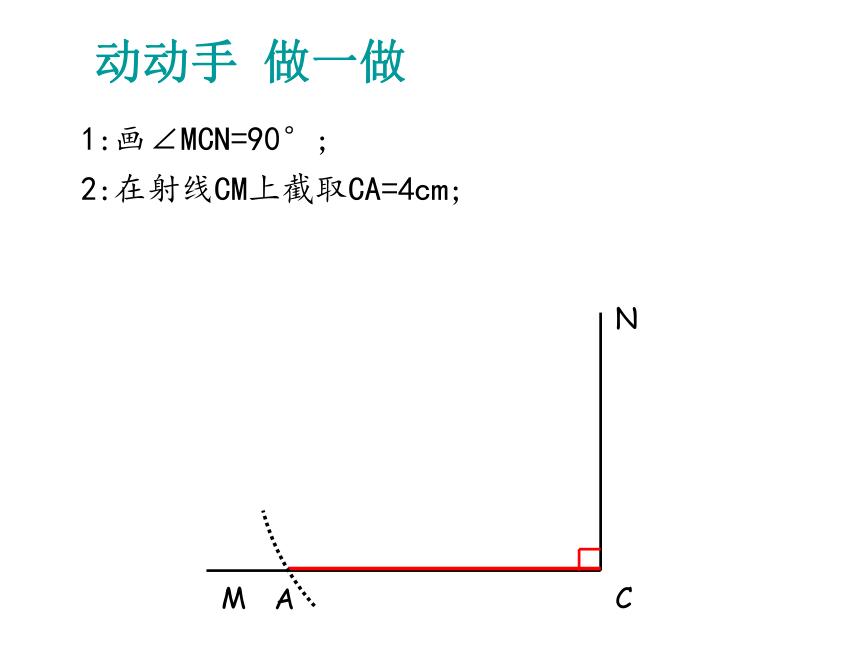
2:在射线CM上截取CA=4cm;
A
1:画∠MCN=90°;
2:在射线CM上截取CA=4cm;
动动手
做一做
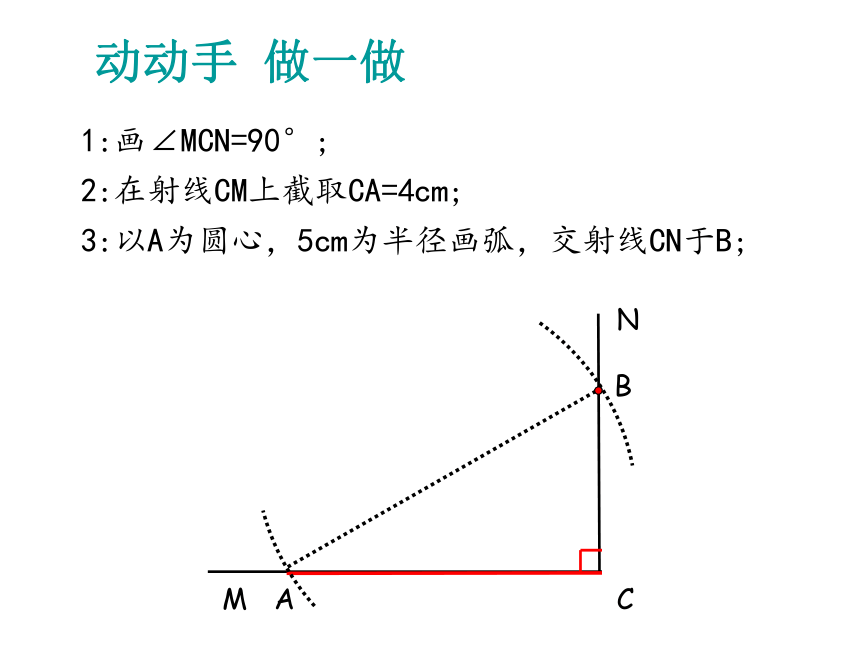
3:以A为圆心,5cm为半径画弧,交射线CN于B;
C
N
M
A
B
1:画∠MCN=90°;
C
N
M
2:在射线CM上截取CA=4cm;
B
动动手
做一做
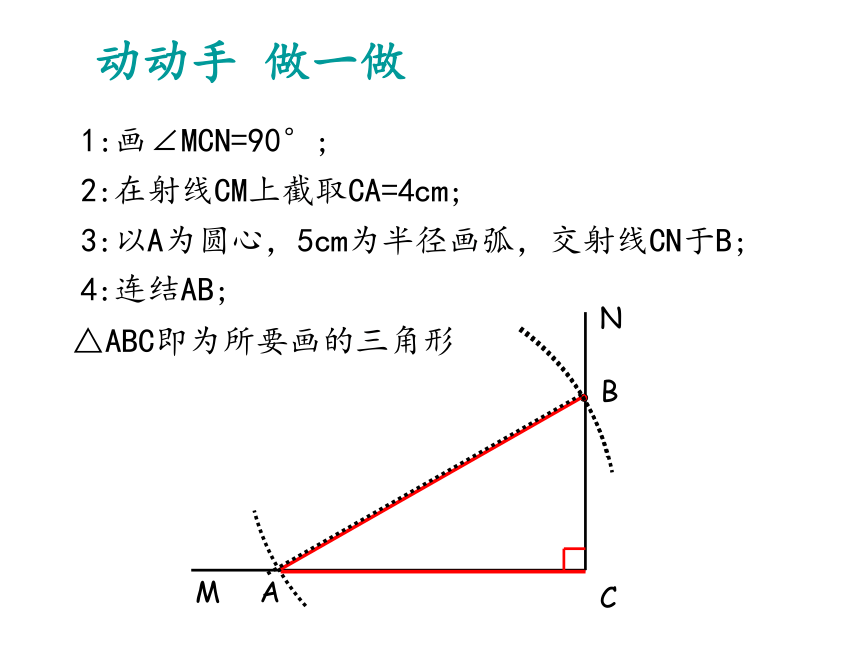
3:以A为圆心,5cm为半径画弧,交射线CN于B;
A
4:连结AB;
△ABC即为所要画的三角形
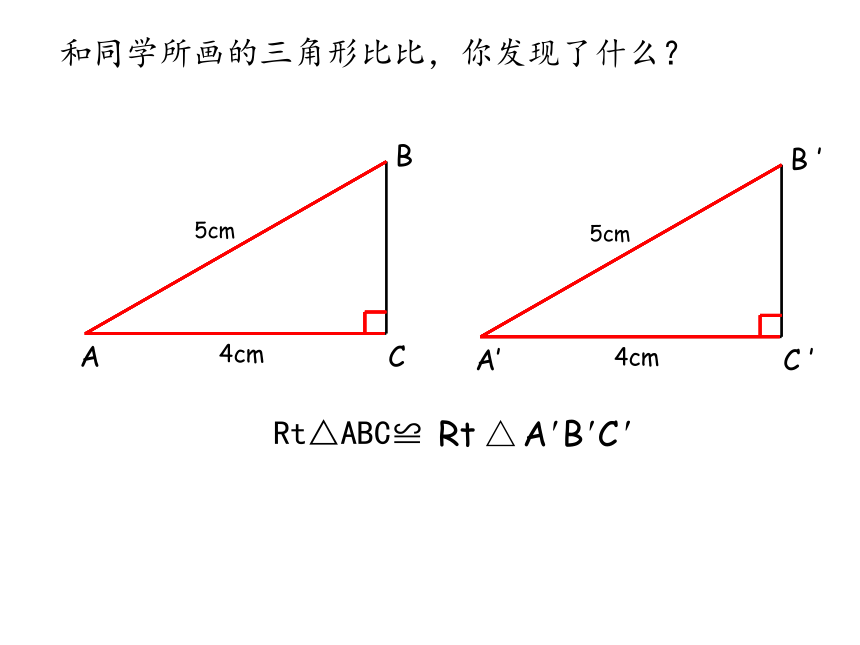
Rt△ABC≌
A
B
C
5cm
4cm
A′
B
′
C
′
5cm
4cm
和同学所画的三角形比比,你发现了什么?
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”
或“HL”
前提
条件1
条件2
斜边、直角边公理
(HL)
A
B
C
A
′
B′
C
′
∴在Rt△ABC和Rt△
中
AB=
BC=
∴Rt△ABC≌
∵∠C=∠C′=90°
有斜边和一条直角边对应相等的两个直角三角形全等.
前提
条件1
条件2
如图,AC=AD,∠C,∠D是直角,你能说明BC与BD相等吗?
C
D
A
B
练习1、如图,∠C
=∠D,请你再添加一个条件,使△ABD
≌
△BAC,并在添加的条件后的(
)内写出判定全等的依据。
(1)
(
)
(2)
(
)
(3)
(
)
(4)
(
)
A
B
D
C
AD=BC
∠
DAB=
∠
CBA
BD=AC
∠
DBA=
∠
CAB
HL
HL
AAS
AAS
例4.如图AB=CD,AE⊥BC,DF⊥BC,CE=BF.求证:AE=DF.
A
B
C
D
E
F
证明:
∵
AE
⊥BC,DF
⊥BC,
∴
∠AEB=∠DFC=90°,
∵CE=BF,
∴CE-EF=BF-EF,
∴
CF=BE.
在Rt△ABE和Rt△DCF中,则
AB=DC,
BE=CF.
∴
Rt△ABE
≌Rt△DCF
(HL).
∴AE=DF
A
B
C
E
D
判断两个直角三角形全等的方法有:
小结
(1):
;
(2):
;
(3):
;
(4):
;
SSS
SAS
ASA
AAS
(5):
;
HL
例5:如图,在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF,求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
∠BAC=∠EDF,
AB=DE,∠B=∠E
分析:
△ABC≌△DEF
Rt△ABP≌Rt△DEQ
AB=DE,AP=DQ
A
B
C
P
D
E
F
Q
证明:∵AP、DQ是△ABC和△DEF的高
∴∠APB=∠DQE=90°
在Rt△ABP和Rt△DEQ中
AB=DE
AP=DQ
∴Rt△ABP≌Rt△DEQ
(HL)
∴
∠B=∠E
在△ABC和△DEF中
∠BAC=∠EDF
AB=DE
∠B=∠E
∴△ABC≌△DEF
(ASA)
作业:金典训练
探索三角形全等的条件
(HL)
忆一忆
1、全等三角形的对应边
---------,
对应角-----------
相等
相等
2、判定三角形全等的方法有:
SAS、ASA、AAS、SSS
直角边
直角边
斜边
3、认识直角三角形
Rt△ABC
有哪些方法可判断两个直角三角形全等?
(1):
;
(2):
;
(3):
;
(4):
;
SSS
SAS
ASA
AAS
你还有其他方法吗?
动动手
做一做
用三角板和圆规,画一个Rt△ABC,使得∠C=90°,一直角边CA=4cm,斜边AB=5cm.
A
B
C
5cm
4cm
动动手
做一做
1:画∠MCN=90°;
C
N
M
动动手
做一做
1:画∠MCN=90°;
C
N
M
2:在射线CM上截取CA=4cm;
A
1:画∠MCN=90°;
2:在射线CM上截取CA=4cm;
动动手
做一做
3:以A为圆心,5cm为半径画弧,交射线CN于B;
C
N
M
A
B
1:画∠MCN=90°;
C
N
M
2:在射线CM上截取CA=4cm;
B
动动手
做一做
3:以A为圆心,5cm为半径画弧,交射线CN于B;
A
4:连结AB;
△ABC即为所要画的三角形
Rt△ABC≌
A
B
C
5cm
4cm
A′
B
′
C
′
5cm
4cm
和同学所画的三角形比比,你发现了什么?
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”
或“HL”
前提
条件1
条件2
斜边、直角边公理
(HL)
A
B
C
A
′
B′
C
′
∴在Rt△ABC和Rt△
中
AB=
BC=
∴Rt△ABC≌
∵∠C=∠C′=90°
有斜边和一条直角边对应相等的两个直角三角形全等.
前提
条件1
条件2
如图,AC=AD,∠C,∠D是直角,你能说明BC与BD相等吗?
C
D
A
B
练习1、如图,∠C
=∠D,请你再添加一个条件,使△ABD
≌
△BAC,并在添加的条件后的(
)内写出判定全等的依据。
(1)
(
)
(2)
(
)
(3)
(
)
(4)
(
)
A
B
D
C
AD=BC
∠
DAB=
∠
CBA
BD=AC
∠
DBA=
∠
CAB
HL
HL
AAS
AAS
例4.如图AB=CD,AE⊥BC,DF⊥BC,CE=BF.求证:AE=DF.
A
B
C
D
E
F
证明:
∵
AE
⊥BC,DF
⊥BC,
∴
∠AEB=∠DFC=90°,
∵CE=BF,
∴CE-EF=BF-EF,
∴
CF=BE.
在Rt△ABE和Rt△DCF中,则
AB=DC,
BE=CF.
∴
Rt△ABE
≌Rt△DCF
(HL).
∴AE=DF
A
B
C
E
D
判断两个直角三角形全等的方法有:
小结
(1):
;
(2):
;
(3):
;
(4):
;
SSS
SAS
ASA
AAS
(5):
;
HL
例5:如图,在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF,求证:△ABC≌△DEF
A
B
C
P
D
E
F
Q
∠BAC=∠EDF,
AB=DE,∠B=∠E
分析:
△ABC≌△DEF
Rt△ABP≌Rt△DEQ
AB=DE,AP=DQ
A
B
C
P
D
E
F
Q
证明:∵AP、DQ是△ABC和△DEF的高
∴∠APB=∠DQE=90°
在Rt△ABP和Rt△DEQ中
AB=DE
AP=DQ
∴Rt△ABP≌Rt△DEQ
(HL)
∴
∠B=∠E
在△ABC和△DEF中
∠BAC=∠EDF
AB=DE
∠B=∠E
∴△ABC≌△DEF
(ASA)
作业:金典训练
