2019-2020学年江西省宜春市高一(下)期末数学试卷(Word含解析)
文档属性
| 名称 | 2019-2020学年江西省宜春市高一(下)期末数学试卷(Word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 243.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 16:59:25 | ||
图片预览




文档简介
2019-2020学年江西省宜春市高一(下)期末数学试卷
一、选择题:本题共12小题,每题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)在下列向量组中,可以把向量=(3,2)表示出来的是( )
A.=(0,0),=(1,2)
B.=(﹣1,2),=(5,﹣2)
C.=(3,5),=(6,10)
D.=(2,﹣3),=(﹣2,3)
2.(5分)12件同类产品中,有10件是正品,2件是次品,从中任意抽出3件,与“抽得1件次品2件正品”互斥而不对立的事件是( )
A.抽得3件正品
B.抽得至少有1件正品
C.抽得至少有1件次品
D.抽得3件正品或2件次品1件正品
3.(5分)某商场一年中各月份的收入、支出(单位:万元)情况的统计如折线图所示,则下列说法正确的是( )
A.1至2月份的收入的变化率与10至11月份的收入的变化率相同
B.支出最高值与支出最低值的比是6:1
C.第三季度平均收入为60万元
D.利润最高的月份是2月份
4.(5分)设θ是第三象限角,且|cos|=﹣cos,则是( )
A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
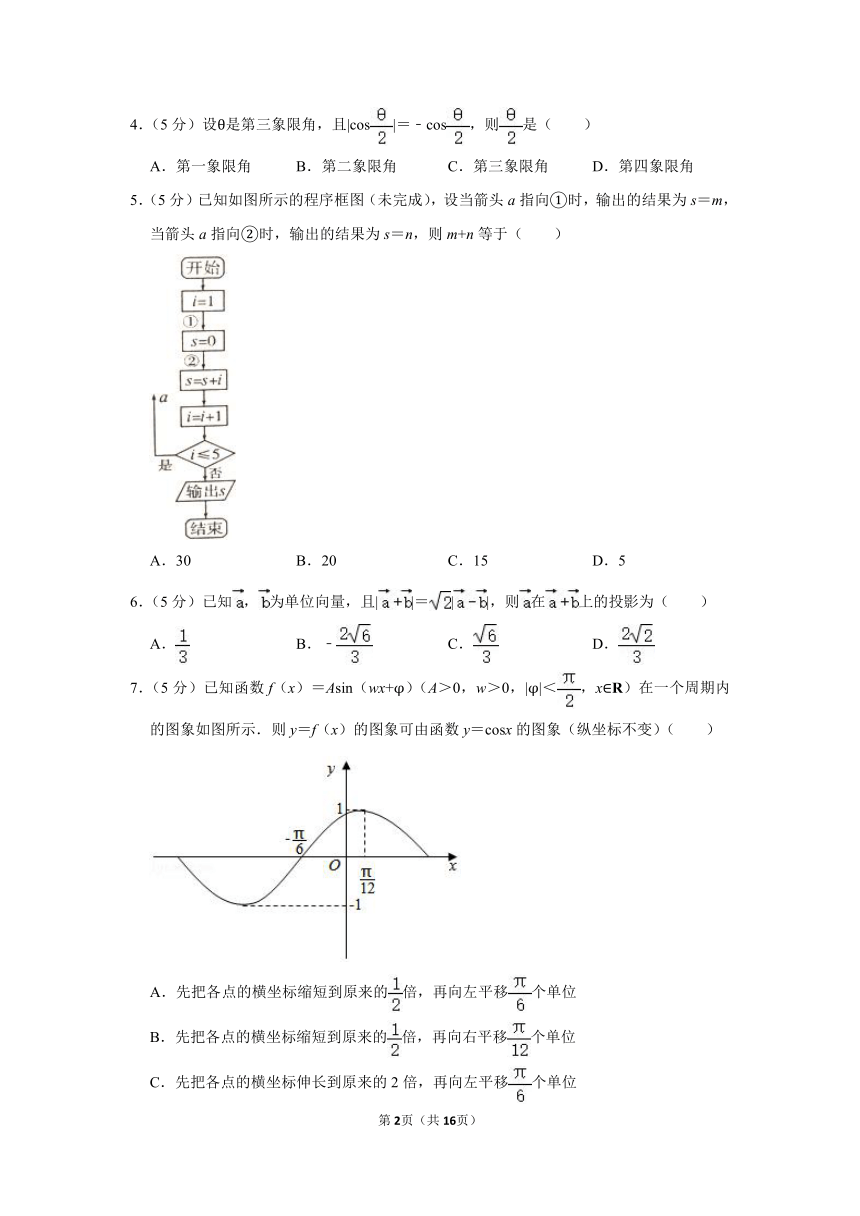
5.(5分)已知如图所示的程序框图(未完成),设当箭头a指向①时,输出的结果为s=m,当箭头a指向②时,输出的结果为s=n,则m+n等于( )
A.30
B.20
C.15
D.5
6.(5分)已知,为单位向量,且||=||,则在上的投影为( )
A.
B.﹣
C.
D.
7.(5分)已知函数f(x)=Asin(wx+φ)(A>0,w>0,|φ|<,x∈R)在一个周期内的图象如图所示.则y=f(x)的图象可由函数y=cosx的图象(纵坐标不变)( )
A.先把各点的横坐标缩短到原来的倍,再向左平移个单位
B.先把各点的横坐标缩短到原来的倍,再向右平移个单位
C.先把各点的横坐标伸长到原来的2倍,再向左平移个单位
D.先把各点的横坐标伸长到原来的2倍,再向右平移个单位
8.(5分)如图,四边形ABCD是边长为2的菱形,∠BAD=60°,E,F分别为BC,CD的中点,则=( )
A.
B.
C.
D.
9.(5分)已知函数f(x)=tan(ωx+φ)(ω≠0,|φ|<),点(,0)和(,0)是其相邻的两个对称中心,具在区间(,)内单调递减,则φ=( )
A.
B.
C.﹣
D.﹣
10.(5分)在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体均值为3,中位数为4
B.乙地:总体均值为1,总体方差大于0
C.丙地:中位数为2,众数为3
D.丁地:总体均值为2,总体方差为3
11.(5分)已知某线路公交车从6:30首发,每5分钟一班,甲、乙两同学都从起点站坐车去学校,若甲每天到起点站的时间是在6:30~7:00任意时刻随机到达,乙每天到起点站的时间是在6:45~7:15任意时刻随机到达,那么甲、乙两人搭乘同一辆公交车的概率是( )
A.
B.
C.
D.
12.(5分)已知O为正三角形ABC内一点,且满足+λ+(1+λ)=0,若△OAB的面积与△OAC的面积比值为3,则λ的值为( )
A.
B.1
C.2
D.3
二、选择题:本题共4小题,每题5分,共20分.
13.(5分)y=lg(2sinx﹣1)+的定义域是
.
14.(5分)运行如图所示程序,若结束时输出的结果不小于3,则t的取值范围为
.
15.(5分)若向量=(2,﹣x)与=(x,﹣8)的夹角为钝角,则x的范围为
.
16.(5分)已知f(x)=sin(ωx+φ+)(ω>0)同时满足下列三个条件:①T=π;
②y=f(x﹣)是奇函数;③f(0)<f(),若f(x)在[0,t)上没有最小值,则实数t的值范围是
.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知在同一平面内,且.
(1)若,且,求;
(2)若,且,求与的夹角的余弦值.
18.(12分)已知向量=(cosωx,2cosωx),=(2sinωx,﹣cosωx),函数f(x)=?+1的图象关于直线x=π对称,其中常数ω∈(,1).
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[0,]上的值域.
19.(12分)据统计某品牌服装专卖店一周内每天获取得纯利润y(百元)与每天销售这种服装件数x(百件)之间有如下一组数据:
x
3
4
5
6
7
8
9
y
66
69
73
81
89
90
91
该专卖店计划在国庆节举行大型促销活动以提高该品牌服装的知名度,为了检验服装的质量,现从厂家购进的500件服装中抽取60件进行检验,(服装进货编号为001﹣500).
(1)利用随机数表抽样本时,如果从随机数表第8行第2列的数开始按三位数连贯向右读取,试写出最先检测的5件服装的编号;
(2)求该专卖店每天的纯利y与每天销售件数x之间的回归直线方程.(精确到0.01)
(3)估计每天销售1200件这种服装时获多少纯利润?
附表:(随机数表第7行至第9行)
84421
75331
57245
50688
77047
44767
21763
35025
83921
20676
63016
47859
16955
56719
98105
07185
12867
35807
44395
23879
33211
23429
78645
60782
52420
74438
15510
01342
99660
27954
参考数据:已知:xi2=280,yi2=45309,xiyi=3487.
参考公式:=,=﹣.
20.(12分)已知cos(α+β)=,tanβ=,且α、.
(1)求cos2β﹣sin2β+sinβcosβ的值;
(2)求2α+β的值.
21.(12分)从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的部分,已知第一组与第八组人数相同,第六组的人数为4人.
(1)求第七组的频率;
(2)估计该校的800名男生的身高的中位数以及身高在180cm以上(含180cm)的人数;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x,y,事件E={|x﹣y|≤5},求P(E).
22.(12分)已知函数f(x)=2cosxsin(x+)﹣2cos2x+,x∈R.
(1)当x∈[0,π]时,求函数f(x)的单调递增区间;
(2)将函数f(x)的图象向左平移个单位后,所得图象对应的函数为h(x),若关于x的方程2[h(x)]2+mh(x)+1=0在区间[0,]上有两个不相等的实根,求实数m的取值范围.
2019-2020学年江西省宜春市高一(下)期末数学试卷
参考答案与试题解析
一、选择题:本题共12小题,每题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【解答】解:根据,
选项A:(3,2)=λ(0,0)+μ(1,2),则
3=μ,2=2μ,无解,故选项A不能;
选项B:(3,2)=λ(﹣1,2)+μ(5,﹣2),则3=﹣λ+5μ,2=2λ﹣2μ,解得,λ=2,μ=1,故选项B能.
选项C:(3,2)=λ(3,5)+μ(6,10),则3=3λ+6μ,2=5λ+10μ,无解,故选项C不能.
选项D:(3,2)=λ(2,﹣3)+μ(﹣2,3),则3=2λ﹣2μ,2=﹣3λ+3μ,无解,故选项D不能.
故选:B.
2.【解答】解:根据题意,得;
对于A,“抽得3件正品”与“抽得1件次品2件正品”是互斥而不对立的事件;
对于B,“抽得至少有1件正品”与“抽得1件次品2件正品”不是互斥事件;
对于C,“抽得至少有1件次品”与“抽得1件次品2件正品”不是互斥事件;
对于D,“抽得3件正品或2件次品1件正品”与“抽得1件次品2件正品”是对立事件.
故选:A.
3.【解答】解:根据图象可知,1至2月份的收入的变化率是30万/月,10至11月份的收入的变化率是20万/月,不相同,所以A错误;
支出最高值是2月60万,支出最低值是5月10万,比是6:1,所以B正确;
第三季度平均收入为(40+50+60)=50万元,所以C错误;
利润最高的月份是3月份和10月份,都是30万元,所以D错误.
故选:B.
4.【解答】解:∵θ是第三象限角,∴在第二象限或在第四象限,
由|cos|=﹣cos,
∴cos≤0,
即在第二象限,
故选:B.
5.【解答】解:当箭头a指向①时,输出的结果s=m,
第1次循环,S=1,i=2
第2次循环,S=2,i=3
第3次循环,S=3,i=4
第4次循环,S=4,i=5
第5次循环,S=5,i=6
不满足6≤5,退出循环,即输出的结果为m=5,
当箭头a指向②时,输出的结果s=n,
第1次循环,S=1,i=2
第2次循环,S=3,i=3
第3次循环,S=6,i=4
第4次循环,S=10,i=5
第5次循环,S=15,i=6
不满足6≤5,退出循环,即输出的结果为n=15,
所以m+n=20.
故选:B.
6.【解答】解:由,为单位向量,知,
再由且||=||,得,
即,
∴.
则=.
.
∴在上的投影为.
故选:C.
7.【解答】解:由函数f(x)=Asin(wx+φ)(A>0,w>0,|φ|<,x∈R)在一个周期内的图象
可得
A=1,==,解得
w=2.
再把点(,1)代入函数的解析式可得
1=sin(2×+φ),即
sin(+φ)=1.
再由|φ|<,可得
φ=,故函数f(x)=sin(2x+).
把函数y=cosx的图象先把各点的横坐标缩短到原来的倍,可得y=cos2x的图象,
再向右平移个单位可得y=cos2(x﹣)=cos(2x﹣)=sin[﹣(2x﹣)]
=sin(﹣2x)=sin[π﹣(﹣2x)]=sin(2x+)=f(x)的图象.
故选:B.
8.【解答】解:四边形ABCD是边长为2的菱形,∠BAD=60°,
可得?=2×2×cos60°=2,
则=(+)?
=(+)?(﹣)
=(×4﹣4+×2)=﹣,
故选:D.
9.【解答】解:函数f(x)=tan(ωx+φ)(ω≠0,|φ|<),
点(,0)和(,0)是其相邻的两个对称中心,
∴?||=﹣,∴ω=±1,f(x)=tan(±x+φ).
∵f(x)在区间(,)内单调递减,故ω=﹣1,f(x)=tan(﹣x+φ),
且f()
不存在,即﹣+φ=mπ+,即
φ=mπ+,m∈Z.
令m=﹣1,可得φ=,
故选:B.
10.【解答】解:∵平均数和中位数不能限制某一天的病例超过7人,
故A不正确,
当总体方差大于0,不知道总体方差的具体数值,因此不能确定数据的波动大小,
故B不正确,
中位数和众数也不能确定,
故C不正确,
当总体平均数是2,若有一个数据超过7,则方差就接近3,
∴总体均值为2,总体方差为3时,没有数据超过7.
故D正确.
故选:D.
11.【解答】解:由题意知本题是一个几何概型,
设甲和乙到达的分别为6时+x分、6时+y分,
则30≤x≤60,45≤y≤75,
他们能搭乘同一班公交车,则45≤x≤60,45≤y≤60.
则试验包含的所有区域是Ω={(x,y)|30≤x≤60,45≤y≤75},
他们能搭乘同一班公交车所表示的区域为A={(x,y)|或或},
则他们能搭乘同一班公交车的概率是:p==.
故选:D.
12.【解答】解:,
变为.
如图,D,E分别是对应边的中点,
由平行四边形法则知
故①
在正三角形ABC中,
∵==,
且三角形AOC与三角形ADC同底边AC,
故O点到底边AC的距离等于D到底边AC的距离的三分之一,
故=,?=﹣②
由①②得λ=.
故选:A.
二、选择题:本题共4小题,每题5分,共20分.
13.【解答】解:∵
∴2sinx﹣1>0
①
1﹣2cosx≥0
②
由①得,sinx>
由②得cosx,
∴,k∈z
故答案为:[
14.【解答】解:模拟程序框图的运行过程,如下;
n=0,x=t,a=1,n=0+2=2,x=2t,a=2﹣1=1;
2>4,否,n=2+2=4,x=4t,a=4﹣1=3;
4>4,否,n=4+2=6,x=8t,a=6﹣3=3;
6>4,是,输出ax=38t;
∵38t≥3,∴8t≥1,即t≥;
∴t的取值范围为{t|t≥}.
故答案为:{t|t≥}.
15.【解答】解:因为向量=(2,﹣x)与=(x,﹣8)的夹角为钝角,所以=2x+8x<0且x2≠16,
所以x<0且x≠﹣4.
故答案为:x<0且x≠﹣4.
16.【解答】解:由函数的周期T==π,
∴ω=2,
由y=f(x﹣)是奇函数可知y=f(x)的图象关于()对称,
所以sin(φ﹣)=0,即φ﹣=kπ,k∈Z,
所以即φ=+kπ,f(x)=sin(2x++kπ),
因为f(0)<f(),所以sin(+kπ)<sin(π+kπ),
当k为偶数时显然不成立,故k为奇数,f(x)=sin(2x++kπ)=sin(2x﹣π),
由x∈[0,t)可得2x﹣,
因为f(x)在[0,t)上没有最小值,
所以2t﹣,
解可得,.
故答案为:(].
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.【解答】解:(1)根据题意,设
则,,则有2x﹣y=0,即y=2x,①
又由,则有x2+y2=45,②
解可得:
∴;
(2)又由,则有,
变形可得,
又,则有,
则有,
故与的夹角的余弦值为.
18.【解答】解:(1)f(x)=?+1=2sinωxcosωx﹣2cos2ωx+1=sin2ωx﹣cos2ωx=2sin(2ωx),
因为图象关于直线x=π对称,
所以2ωπ=即ω=,其中常数ω∈(,1),
∴ω=,T=,f(x)=2sin(),
(2)由可得,
所以﹣sin()≤1,
故函数的值域[﹣1,2].
19.【解答】解:(1)利用随机数表抽样本方法,可得最先检测的5件服装的编号为:
301,169,105,071,286;
(2)根据表中数据,计算得=×(3+4+5+6+7+8+9)=6,
=×(66+69+73+81+89+90+91)=,
xi2=280,xiyi=3487,
计算===4.75,
==,
∴每天的纯利润y与每天销售件数x的回归方程为=4.75x+51.36;
(3)当x=12时,=4.75×12+51.36=108.36百元;
估计每天销售1200件这种服装时,获得利润是10836元.
20.【解答】解:(1)已知cos(α+β)=,tanβ=,且α、.
所以0<α+β<π,
故,tan(α+β)=,
由于=,解得tan.
所以cos2β﹣sin2β+sinβcosβ===.
(2)tan(2α+β)=tan[(α+β)+α]==.
所以2α+β=.
21.【解答】解:(1)∵第六组的人数为4人,∴第六组的频率为=0.08,
∴第七组的频率为1﹣(0.008+0.016+0.04+0.04+0.06+0.008)×5﹣0.08=0.06.
(2)∵身高介于155cm和170cm之间的频率为(0.008+0.016+0.04)×5=0.32,
身高介于155cm和175cm之间的频率为(0.008+0.016+0.04+0.04)×5=0.52,
而0.32<0.5<0.52,
∴该校800名男生的身高的中位数在区间[170,175)内.
设中位数为x,则0.32+(x﹣170)×0.04=0.5,解之得x=174.5,
∴该校的800名男生的身高的中位数为174.5.
由(1)可知,第六组和第七组的频率分别为0.08和0.06,
∴50名男生中,身高在180cm以上(含180cm)的人数为50×(0.08+0.06+0.008×5)=9人,
故该校800名男生的身高在180cm以上(含180cm)的人数为800×=144人.
(3)第六组的人数为50×0.08=4人,设为a,b,c,d;
第八组的人数为50×0.008×5=2人,设为A,B.
从中随机抽取两名男生,共有15种情况,分别为ab,ac,ad,aA,aB,bc,bd,bA,bB,cd,cA,cB,AB,dA,dB;
事件E发生时,两名男生在同一组,包含7种情况,分别为ab,ac,ad,bc,bd,cd,AB.
故P(E)=.
22.【解答】解:(1)函数f(x)=2cosxsin(x+)﹣2cos2x+=2cosx(sinx+cosx)﹣2cos2x+
=sinxosx﹣cos2x+=sin2x﹣?+=sin(2x﹣),x∈R,
令2kπ﹣≤2x﹣≤2kπ+,求得
kπ﹣≤x≤kπ+,
可得函数f(x)的增区间为[kπ﹣,kπ+],k∈Z.
再结合x∈[0,π],可得函数f(x)的增区间为[0,],[,π].
(2)将函数f(x)的图象向左平移个单位后,所得图象对应的函数为h(x)=sin2x,
若关于x的方程2[h(x)]2+mh(x)+1=0在区间[0,]上有两个不相等的实根,
即
2sin22x+msin2x+1=0在区间[0,]上有两个不相等的实根.
令t=sin2x,则2t2+mt+1=0
在区间[0,1)上有1个根.
令g(t)=2t2+mt+1,则g(0)g(1)=1×(m+3)<0,或,
求得m<﹣3,或﹣4<m<﹣3,
即实数m的范围为(﹣∞,﹣3).
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/8
9:31:57;用户:bawxf007;邮箱:bawxf007@126.com;学号:4165708
一、选择题:本题共12小题,每题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)在下列向量组中,可以把向量=(3,2)表示出来的是( )
A.=(0,0),=(1,2)
B.=(﹣1,2),=(5,﹣2)
C.=(3,5),=(6,10)
D.=(2,﹣3),=(﹣2,3)
2.(5分)12件同类产品中,有10件是正品,2件是次品,从中任意抽出3件,与“抽得1件次品2件正品”互斥而不对立的事件是( )
A.抽得3件正品
B.抽得至少有1件正品
C.抽得至少有1件次品
D.抽得3件正品或2件次品1件正品
3.(5分)某商场一年中各月份的收入、支出(单位:万元)情况的统计如折线图所示,则下列说法正确的是( )
A.1至2月份的收入的变化率与10至11月份的收入的变化率相同
B.支出最高值与支出最低值的比是6:1
C.第三季度平均收入为60万元
D.利润最高的月份是2月份
4.(5分)设θ是第三象限角,且|cos|=﹣cos,则是( )
A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
5.(5分)已知如图所示的程序框图(未完成),设当箭头a指向①时,输出的结果为s=m,当箭头a指向②时,输出的结果为s=n,则m+n等于( )
A.30
B.20
C.15
D.5
6.(5分)已知,为单位向量,且||=||,则在上的投影为( )
A.
B.﹣
C.
D.
7.(5分)已知函数f(x)=Asin(wx+φ)(A>0,w>0,|φ|<,x∈R)在一个周期内的图象如图所示.则y=f(x)的图象可由函数y=cosx的图象(纵坐标不变)( )
A.先把各点的横坐标缩短到原来的倍,再向左平移个单位
B.先把各点的横坐标缩短到原来的倍,再向右平移个单位
C.先把各点的横坐标伸长到原来的2倍,再向左平移个单位
D.先把各点的横坐标伸长到原来的2倍,再向右平移个单位
8.(5分)如图,四边形ABCD是边长为2的菱形,∠BAD=60°,E,F分别为BC,CD的中点,则=( )
A.
B.
C.
D.
9.(5分)已知函数f(x)=tan(ωx+φ)(ω≠0,|φ|<),点(,0)和(,0)是其相邻的两个对称中心,具在区间(,)内单调递减,则φ=( )
A.
B.
C.﹣
D.﹣
10.(5分)在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体均值为3,中位数为4
B.乙地:总体均值为1,总体方差大于0
C.丙地:中位数为2,众数为3
D.丁地:总体均值为2,总体方差为3
11.(5分)已知某线路公交车从6:30首发,每5分钟一班,甲、乙两同学都从起点站坐车去学校,若甲每天到起点站的时间是在6:30~7:00任意时刻随机到达,乙每天到起点站的时间是在6:45~7:15任意时刻随机到达,那么甲、乙两人搭乘同一辆公交车的概率是( )
A.
B.
C.
D.
12.(5分)已知O为正三角形ABC内一点,且满足+λ+(1+λ)=0,若△OAB的面积与△OAC的面积比值为3,则λ的值为( )
A.
B.1
C.2
D.3
二、选择题:本题共4小题,每题5分,共20分.
13.(5分)y=lg(2sinx﹣1)+的定义域是
.
14.(5分)运行如图所示程序,若结束时输出的结果不小于3,则t的取值范围为
.
15.(5分)若向量=(2,﹣x)与=(x,﹣8)的夹角为钝角,则x的范围为
.
16.(5分)已知f(x)=sin(ωx+φ+)(ω>0)同时满足下列三个条件:①T=π;
②y=f(x﹣)是奇函数;③f(0)<f(),若f(x)在[0,t)上没有最小值,则实数t的值范围是
.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知在同一平面内,且.
(1)若,且,求;
(2)若,且,求与的夹角的余弦值.
18.(12分)已知向量=(cosωx,2cosωx),=(2sinωx,﹣cosωx),函数f(x)=?+1的图象关于直线x=π对称,其中常数ω∈(,1).
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[0,]上的值域.
19.(12分)据统计某品牌服装专卖店一周内每天获取得纯利润y(百元)与每天销售这种服装件数x(百件)之间有如下一组数据:
x
3
4
5
6
7
8
9
y
66
69
73
81
89
90
91
该专卖店计划在国庆节举行大型促销活动以提高该品牌服装的知名度,为了检验服装的质量,现从厂家购进的500件服装中抽取60件进行检验,(服装进货编号为001﹣500).
(1)利用随机数表抽样本时,如果从随机数表第8行第2列的数开始按三位数连贯向右读取,试写出最先检测的5件服装的编号;
(2)求该专卖店每天的纯利y与每天销售件数x之间的回归直线方程.(精确到0.01)
(3)估计每天销售1200件这种服装时获多少纯利润?
附表:(随机数表第7行至第9行)
84421
75331
57245
50688
77047
44767
21763
35025
83921
20676
63016
47859
16955
56719
98105
07185
12867
35807
44395
23879
33211
23429
78645
60782
52420
74438
15510
01342
99660
27954
参考数据:已知:xi2=280,yi2=45309,xiyi=3487.
参考公式:=,=﹣.
20.(12分)已知cos(α+β)=,tanβ=,且α、.
(1)求cos2β﹣sin2β+sinβcosβ的值;
(2)求2α+β的值.
21.(12分)从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的部分,已知第一组与第八组人数相同,第六组的人数为4人.
(1)求第七组的频率;
(2)估计该校的800名男生的身高的中位数以及身高在180cm以上(含180cm)的人数;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x,y,事件E={|x﹣y|≤5},求P(E).
22.(12分)已知函数f(x)=2cosxsin(x+)﹣2cos2x+,x∈R.
(1)当x∈[0,π]时,求函数f(x)的单调递增区间;
(2)将函数f(x)的图象向左平移个单位后,所得图象对应的函数为h(x),若关于x的方程2[h(x)]2+mh(x)+1=0在区间[0,]上有两个不相等的实根,求实数m的取值范围.
2019-2020学年江西省宜春市高一(下)期末数学试卷
参考答案与试题解析
一、选择题:本题共12小题,每题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【解答】解:根据,
选项A:(3,2)=λ(0,0)+μ(1,2),则
3=μ,2=2μ,无解,故选项A不能;
选项B:(3,2)=λ(﹣1,2)+μ(5,﹣2),则3=﹣λ+5μ,2=2λ﹣2μ,解得,λ=2,μ=1,故选项B能.
选项C:(3,2)=λ(3,5)+μ(6,10),则3=3λ+6μ,2=5λ+10μ,无解,故选项C不能.
选项D:(3,2)=λ(2,﹣3)+μ(﹣2,3),则3=2λ﹣2μ,2=﹣3λ+3μ,无解,故选项D不能.
故选:B.
2.【解答】解:根据题意,得;
对于A,“抽得3件正品”与“抽得1件次品2件正品”是互斥而不对立的事件;
对于B,“抽得至少有1件正品”与“抽得1件次品2件正品”不是互斥事件;
对于C,“抽得至少有1件次品”与“抽得1件次品2件正品”不是互斥事件;
对于D,“抽得3件正品或2件次品1件正品”与“抽得1件次品2件正品”是对立事件.
故选:A.
3.【解答】解:根据图象可知,1至2月份的收入的变化率是30万/月,10至11月份的收入的变化率是20万/月,不相同,所以A错误;
支出最高值是2月60万,支出最低值是5月10万,比是6:1,所以B正确;
第三季度平均收入为(40+50+60)=50万元,所以C错误;
利润最高的月份是3月份和10月份,都是30万元,所以D错误.
故选:B.
4.【解答】解:∵θ是第三象限角,∴在第二象限或在第四象限,
由|cos|=﹣cos,
∴cos≤0,
即在第二象限,
故选:B.
5.【解答】解:当箭头a指向①时,输出的结果s=m,
第1次循环,S=1,i=2
第2次循环,S=2,i=3
第3次循环,S=3,i=4
第4次循环,S=4,i=5
第5次循环,S=5,i=6
不满足6≤5,退出循环,即输出的结果为m=5,
当箭头a指向②时,输出的结果s=n,
第1次循环,S=1,i=2
第2次循环,S=3,i=3
第3次循环,S=6,i=4
第4次循环,S=10,i=5
第5次循环,S=15,i=6
不满足6≤5,退出循环,即输出的结果为n=15,
所以m+n=20.
故选:B.
6.【解答】解:由,为单位向量,知,
再由且||=||,得,
即,
∴.
则=.
.
∴在上的投影为.
故选:C.
7.【解答】解:由函数f(x)=Asin(wx+φ)(A>0,w>0,|φ|<,x∈R)在一个周期内的图象
可得
A=1,==,解得
w=2.
再把点(,1)代入函数的解析式可得
1=sin(2×+φ),即
sin(+φ)=1.
再由|φ|<,可得
φ=,故函数f(x)=sin(2x+).
把函数y=cosx的图象先把各点的横坐标缩短到原来的倍,可得y=cos2x的图象,
再向右平移个单位可得y=cos2(x﹣)=cos(2x﹣)=sin[﹣(2x﹣)]
=sin(﹣2x)=sin[π﹣(﹣2x)]=sin(2x+)=f(x)的图象.
故选:B.
8.【解答】解:四边形ABCD是边长为2的菱形,∠BAD=60°,
可得?=2×2×cos60°=2,
则=(+)?
=(+)?(﹣)
=(×4﹣4+×2)=﹣,
故选:D.
9.【解答】解:函数f(x)=tan(ωx+φ)(ω≠0,|φ|<),
点(,0)和(,0)是其相邻的两个对称中心,
∴?||=﹣,∴ω=±1,f(x)=tan(±x+φ).
∵f(x)在区间(,)内单调递减,故ω=﹣1,f(x)=tan(﹣x+φ),
且f()
不存在,即﹣+φ=mπ+,即
φ=mπ+,m∈Z.
令m=﹣1,可得φ=,
故选:B.
10.【解答】解:∵平均数和中位数不能限制某一天的病例超过7人,
故A不正确,
当总体方差大于0,不知道总体方差的具体数值,因此不能确定数据的波动大小,
故B不正确,
中位数和众数也不能确定,
故C不正确,
当总体平均数是2,若有一个数据超过7,则方差就接近3,
∴总体均值为2,总体方差为3时,没有数据超过7.
故D正确.
故选:D.
11.【解答】解:由题意知本题是一个几何概型,
设甲和乙到达的分别为6时+x分、6时+y分,
则30≤x≤60,45≤y≤75,
他们能搭乘同一班公交车,则45≤x≤60,45≤y≤60.
则试验包含的所有区域是Ω={(x,y)|30≤x≤60,45≤y≤75},
他们能搭乘同一班公交车所表示的区域为A={(x,y)|或或},
则他们能搭乘同一班公交车的概率是:p==.
故选:D.
12.【解答】解:,
变为.
如图,D,E分别是对应边的中点,
由平行四边形法则知
故①
在正三角形ABC中,
∵==,
且三角形AOC与三角形ADC同底边AC,
故O点到底边AC的距离等于D到底边AC的距离的三分之一,
故=,?=﹣②
由①②得λ=.
故选:A.
二、选择题:本题共4小题,每题5分,共20分.
13.【解答】解:∵
∴2sinx﹣1>0
①
1﹣2cosx≥0
②
由①得,sinx>
由②得cosx,
∴,k∈z
故答案为:[
14.【解答】解:模拟程序框图的运行过程,如下;
n=0,x=t,a=1,n=0+2=2,x=2t,a=2﹣1=1;
2>4,否,n=2+2=4,x=4t,a=4﹣1=3;
4>4,否,n=4+2=6,x=8t,a=6﹣3=3;
6>4,是,输出ax=38t;
∵38t≥3,∴8t≥1,即t≥;
∴t的取值范围为{t|t≥}.
故答案为:{t|t≥}.
15.【解答】解:因为向量=(2,﹣x)与=(x,﹣8)的夹角为钝角,所以=2x+8x<0且x2≠16,
所以x<0且x≠﹣4.
故答案为:x<0且x≠﹣4.
16.【解答】解:由函数的周期T==π,
∴ω=2,
由y=f(x﹣)是奇函数可知y=f(x)的图象关于()对称,
所以sin(φ﹣)=0,即φ﹣=kπ,k∈Z,
所以即φ=+kπ,f(x)=sin(2x++kπ),
因为f(0)<f(),所以sin(+kπ)<sin(π+kπ),
当k为偶数时显然不成立,故k为奇数,f(x)=sin(2x++kπ)=sin(2x﹣π),
由x∈[0,t)可得2x﹣,
因为f(x)在[0,t)上没有最小值,
所以2t﹣,
解可得,.
故答案为:(].
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.【解答】解:(1)根据题意,设
则,,则有2x﹣y=0,即y=2x,①
又由,则有x2+y2=45,②
解可得:
∴;
(2)又由,则有,
变形可得,
又,则有,
则有,
故与的夹角的余弦值为.
18.【解答】解:(1)f(x)=?+1=2sinωxcosωx﹣2cos2ωx+1=sin2ωx﹣cos2ωx=2sin(2ωx),
因为图象关于直线x=π对称,
所以2ωπ=即ω=,其中常数ω∈(,1),
∴ω=,T=,f(x)=2sin(),
(2)由可得,
所以﹣sin()≤1,
故函数的值域[﹣1,2].
19.【解答】解:(1)利用随机数表抽样本方法,可得最先检测的5件服装的编号为:
301,169,105,071,286;
(2)根据表中数据,计算得=×(3+4+5+6+7+8+9)=6,
=×(66+69+73+81+89+90+91)=,
xi2=280,xiyi=3487,
计算===4.75,
==,
∴每天的纯利润y与每天销售件数x的回归方程为=4.75x+51.36;
(3)当x=12时,=4.75×12+51.36=108.36百元;
估计每天销售1200件这种服装时,获得利润是10836元.
20.【解答】解:(1)已知cos(α+β)=,tanβ=,且α、.
所以0<α+β<π,
故,tan(α+β)=,
由于=,解得tan.
所以cos2β﹣sin2β+sinβcosβ===.
(2)tan(2α+β)=tan[(α+β)+α]==.
所以2α+β=.
21.【解答】解:(1)∵第六组的人数为4人,∴第六组的频率为=0.08,
∴第七组的频率为1﹣(0.008+0.016+0.04+0.04+0.06+0.008)×5﹣0.08=0.06.
(2)∵身高介于155cm和170cm之间的频率为(0.008+0.016+0.04)×5=0.32,
身高介于155cm和175cm之间的频率为(0.008+0.016+0.04+0.04)×5=0.52,
而0.32<0.5<0.52,
∴该校800名男生的身高的中位数在区间[170,175)内.
设中位数为x,则0.32+(x﹣170)×0.04=0.5,解之得x=174.5,
∴该校的800名男生的身高的中位数为174.5.
由(1)可知,第六组和第七组的频率分别为0.08和0.06,
∴50名男生中,身高在180cm以上(含180cm)的人数为50×(0.08+0.06+0.008×5)=9人,
故该校800名男生的身高在180cm以上(含180cm)的人数为800×=144人.
(3)第六组的人数为50×0.08=4人,设为a,b,c,d;
第八组的人数为50×0.008×5=2人,设为A,B.
从中随机抽取两名男生,共有15种情况,分别为ab,ac,ad,aA,aB,bc,bd,bA,bB,cd,cA,cB,AB,dA,dB;
事件E发生时,两名男生在同一组,包含7种情况,分别为ab,ac,ad,bc,bd,cd,AB.
故P(E)=.
22.【解答】解:(1)函数f(x)=2cosxsin(x+)﹣2cos2x+=2cosx(sinx+cosx)﹣2cos2x+
=sinxosx﹣cos2x+=sin2x﹣?+=sin(2x﹣),x∈R,
令2kπ﹣≤2x﹣≤2kπ+,求得
kπ﹣≤x≤kπ+,
可得函数f(x)的增区间为[kπ﹣,kπ+],k∈Z.
再结合x∈[0,π],可得函数f(x)的增区间为[0,],[,π].
(2)将函数f(x)的图象向左平移个单位后,所得图象对应的函数为h(x)=sin2x,
若关于x的方程2[h(x)]2+mh(x)+1=0在区间[0,]上有两个不相等的实根,
即
2sin22x+msin2x+1=0在区间[0,]上有两个不相等的实根.
令t=sin2x,则2t2+mt+1=0
在区间[0,1)上有1个根.
令g(t)=2t2+mt+1,则g(0)g(1)=1×(m+3)<0,或,
求得m<﹣3,或﹣4<m<﹣3,
即实数m的范围为(﹣∞,﹣3).
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/8
9:31:57;用户:bawxf007;邮箱:bawxf007@126.com;学号:4165708
同课章节目录
