高中数学 人教A版(2019)必修 第一册 第一章 集合与常用逻辑用语 1.3 集合的基本运算 教案 教师版
文档属性
| 名称 | 高中数学 人教A版(2019)必修 第一册 第一章 集合与常用逻辑用语 1.3 集合的基本运算 教案 教师版 | 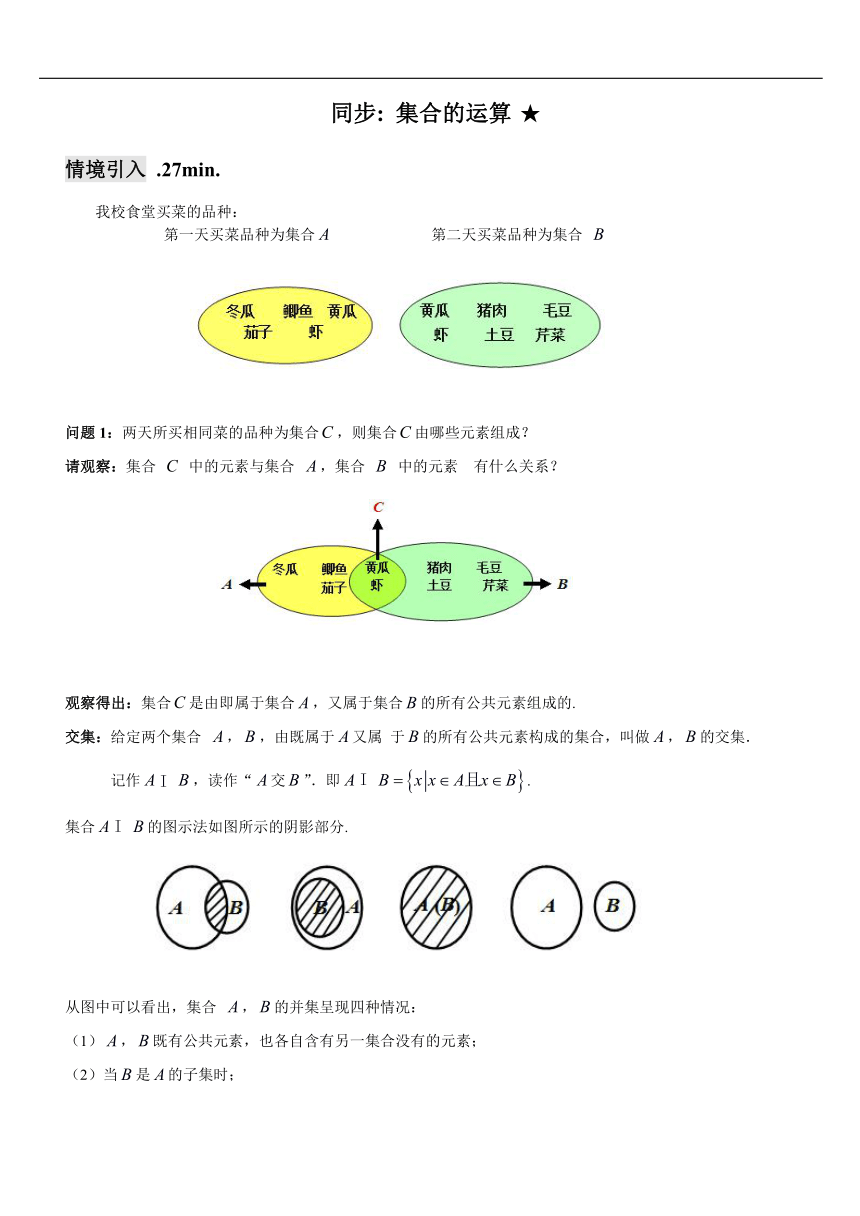 | |
| 格式 | doc | ||
| 文件大小 | 540.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 10:18:35 | ||
图片预览

文档简介
同步: 集合的运算 ★
情境引入 .27min.
我校食堂买菜的品种:
第一天买菜品种为集合 第二天买菜品种为集合
问题1:两天所买相同菜的品种为集合,则集合由哪些元素组成?
请观察:集合 中的元素与集合 ,集合 中的元素 有什么关系?
观察得出:集合是由即属于集合,又属于集合的所有公共元素组成的.
交集:给定两个集合 ,,由既属于又属 于的所有公共元素构成的集合,叫做,的交集.
记作,读作“交”.即.
集合的图示法如图所示的阴影部分.
从图中可以看出,集合 ,的并集呈现四种情况:
(1),既有公共元素,也各自含有另一集合没有的元素;
(2)当是的子集时;
,相等时.
,没有公共元素时;
例1.(★)设两个集合分别为,,则:= ; .
解:,.
问题2:两天买过的所有菜的品种为集合,则集合由哪些元素组成?
请观察:集合 中的元素与集合,集合中的元素有什么关系?
观察得出:集合是由由属于或属 于的所有元素组成的.
并集:给定两个集合 ,,由属于或属于的所有元素构成的集合,叫做,的并集.
记作,读作“并”.即.
集合的图示法如图所示的阴影部分.
从图中可以看出,集合 ,的并集呈现四种情况:
,没有公共元素时;
(2) ,既有公共元素,也各自含有另一集合没有的元素;
(3)当 是的子集时;
(4) ,相等时.
例2. (★)已知,求.
解:.
补集:一般地设为全集,是的一个子集,则由中所有不属于的元素组成的集合叫做集合在全集中的补集.记作,读作“补”.即.
集合的图示法如图所示的蓝色阴影部分.
例3. (★)设,,写出.
解:
课堂练习 .10min.
(★)新华中学开运动会,设是新华中学高一年级参加百米赛跑的同学,是新华中学高一年级参加跳高比赛的同学,求.
解:是新华中学高一年级既参加百米赛跑又参加跳高比赛的同学.
(★)设那么等于( ).
B. C. D.
解:B
(★)设集合,集合,求.
解: ==.
(★),,则= ,= .
解:,
(★)设是小于9的正整数,,,求.
解:根据题意可知,所以 ,.
回顾总结.3min.
PAGE
情境引入 .27min.
我校食堂买菜的品种:
第一天买菜品种为集合 第二天买菜品种为集合
问题1:两天所买相同菜的品种为集合,则集合由哪些元素组成?
请观察:集合 中的元素与集合 ,集合 中的元素 有什么关系?
观察得出:集合是由即属于集合,又属于集合的所有公共元素组成的.
交集:给定两个集合 ,,由既属于又属 于的所有公共元素构成的集合,叫做,的交集.
记作,读作“交”.即.
集合的图示法如图所示的阴影部分.
从图中可以看出,集合 ,的并集呈现四种情况:
(1),既有公共元素,也各自含有另一集合没有的元素;
(2)当是的子集时;
,相等时.
,没有公共元素时;
例1.(★)设两个集合分别为,,则:= ; .
解:,.
问题2:两天买过的所有菜的品种为集合,则集合由哪些元素组成?
请观察:集合 中的元素与集合,集合中的元素有什么关系?
观察得出:集合是由由属于或属 于的所有元素组成的.
并集:给定两个集合 ,,由属于或属于的所有元素构成的集合,叫做,的并集.
记作,读作“并”.即.
集合的图示法如图所示的阴影部分.
从图中可以看出,集合 ,的并集呈现四种情况:
,没有公共元素时;
(2) ,既有公共元素,也各自含有另一集合没有的元素;
(3)当 是的子集时;
(4) ,相等时.
例2. (★)已知,求.
解:.
补集:一般地设为全集,是的一个子集,则由中所有不属于的元素组成的集合叫做集合在全集中的补集.记作,读作“补”.即.
集合的图示法如图所示的蓝色阴影部分.
例3. (★)设,,写出.
解:
课堂练习 .10min.
(★)新华中学开运动会,设是新华中学高一年级参加百米赛跑的同学,是新华中学高一年级参加跳高比赛的同学,求.
解:是新华中学高一年级既参加百米赛跑又参加跳高比赛的同学.
(★)设那么等于( ).
B. C. D.
解:B
(★)设集合,集合,求.
解: ==.
(★),,则= ,= .
解:,
(★)设是小于9的正整数,,,求.
解:根据题意可知,所以 ,.
回顾总结.3min.
PAGE
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
