人教版(2019)高中物理 选择性必修第一册 第2章 第6节 受迫振动共振课件
文档属性
| 名称 | 人教版(2019)高中物理 选择性必修第一册 第2章 第6节 受迫振动共振课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-08 14:41:46 | ||
图片预览











文档简介
第6节 受迫振动 共振
核心素养
物理观念
科学思维
1.了解受迫振动、阻尼振动、固有频率的概念。
2.掌握受迫振动的频率由驱动力的频率决定。
3.知道共振发生的条件以及应用共振和防止共振的事例与方法。
观察演示实验,明确受迫振动的频率决定于驱动力的频率。
知识点一 振动中的能量损失
[观图助学]
生活中会见到阵风吹过树枝,使树枝左右摇摆,一会儿树枝就会停下来。而荡秋千的小朋友如无外界的帮助也会逐渐停下来。
(1)树枝的运动是什么运动?
(2)秋千的摆动是什么运动?
答案 (1)阻尼振动 (2)阻尼振动
1.固有振动和固有频率
如果振动系统没有______干预,此时的振动叫作固有振动,其振动频率称为__________。
2.阻尼振动
实际的振动系统都会受到摩擦、黏滞力等______作用,______必然逐渐减小,这种______随时间逐渐减小的振动,称为阻尼振动。
外力
固有频率
阻碍
振幅
振幅
1.驱动力
如果存在阻尼作用,振动系统最终会停止振动。为了使系统持续振动下去,对振动系统施加的周期性的______,外力对系统______,______系统的能量损耗,这种________的外力叫作驱动力。
2.受迫振动
(1)定义:系统在________作用下的振动,叫作受迫振动。
(2)受迫振动的频率(周期)
做受迫振动的物体,其振动频率总等于________的频率,与物体的__________无关。
知识点二 受迫振动
外力
做功
补偿
周期性
驱动力
驱动力
固有频率
知识点三 共振现象及其应用
[观图助学]
如图所示,先让A摆振动起来,A会通过张紧的绳子给其他各摆施加驱动力,B、C、D三个摆在驱动力作用下开始摆动:
(1)B、C、D三摆的频率有什么关系?
(2)观察B、C、D三摆的振幅,哪一个摆的振幅最大?摆的振幅与固有频率有什么关系。
提示 (1)B、C、D三摆都在做受迫振动,其频率都等于A摆的频率。
(2)B摆的振幅最大;在B、C、D三个摆中,A摆和B摆的摆长相等,故A摆的固有频率等于B摆的固有频率,由实验现象可知当A摆施加的驱动力的频率等于B摆的固有频率时,B摆的振幅最大。即受迫振动摆的振幅与本身固有频率和驱动力频率有关,固有频率越接近驱动力频率,受迫振动摆的振幅越大。
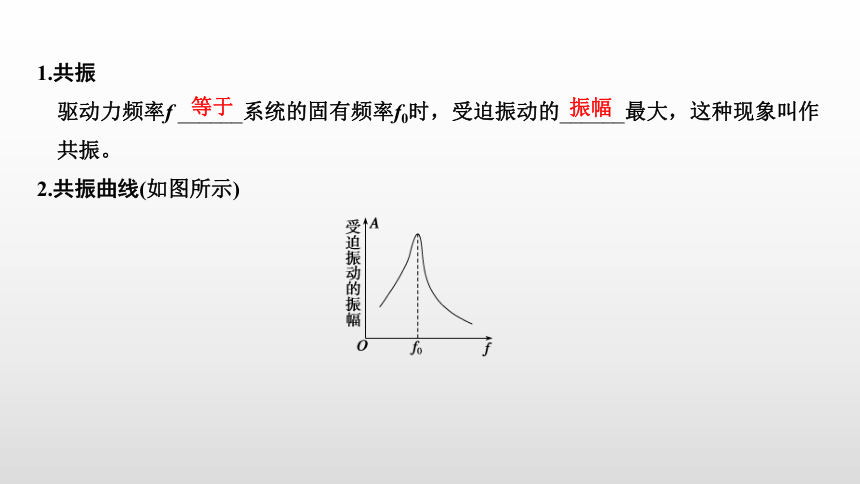
1.共振
驱动力频率f ______系统的固有频率f0时,受迫振动的______最大,这种现象叫作共振。
2.共振曲线(如图所示)
等于
振幅
3.共振的防止与利用
(1)利用:由共振的条件知,要利用共振,就应尽量使驱动力的频率与物体的固有频率一致。如共振筛、荡秋千、共振转速计等。
(2)防止:由共振曲线可知,在需要防止共振危害时,要尽量使驱动力的频率和固有频率不相等,而且相差越多越好。如:部队过桥应便步走。
说明:共振是物体做受迫振动时的一种特殊现象。
[思考判断]
(1)受迫振动的频率与振动系统的固有频率无关。( )
(2)驱动力频率越大,振幅越大。 ( )
(3)共振只有害处没有好处。( )
(4)做受迫振动的物体一定会发生共振。( )
(5)阻尼振动的频率随振幅的减小而不断减小。( )
√
×
×
×
×
1.同一简谐运动能量的大小由振幅大小确定,阻尼振动振幅减小的快慢跟所受阻尼的大小有关,阻尼越大,振幅减小得越快。
2.物体做阻尼振动时,振动的频率仍由自身结构特点所决定,并不会随振幅的减小而变化。例如用力敲锣,由于锣受到空气的阻尼作用,振幅越来越小,锣声减弱,但音调不变。
[要点归纳]
核心要点
阻尼振动
[试题案例]
[例1] (多选)一单摆在空气中振动,振幅逐渐减小,下列说法正确的是( )
A.单摆的机械能逐渐转化为其他形式的能
B.单摆后一时刻的动能一定小于前一时刻的动能
C.单摆振幅减小,频率也随着减小
D.单摆振幅虽然减小,但其频率不变
解析 单摆做阻尼振动,因不断克服空气阻力做功使机械能转化为其他形式的能,但是在振动过程中,动能和势能仍不断相互转化,单摆在从最大位移处向平衡位置运动的过程中,后一时刻的动能大于前一时刻的动能,故选项A正确,B错误;做阻尼振动的物体,频率由系统的特征决定,与振幅无关,所以其频率不变,选项C错误,D正确。
答案 AD
方法凝炼
理解阻尼振动要从两个方面入手:一是从振动能量上来讲,由于阻力做功,振动物体的机械能逐渐减小,振幅逐渐变小,但由于振动中动能与势能相互转化,不能说下一时刻的动能(或势能)变小;二是从振动周期、频率上看,周期与频率由振动系统本身决定,阻尼振动中周期、频率不变。
[针对训练1] (多选)将一个电动传感器接到计算机上,就可以测量快速变化的力,用这种方法测得的某单摆摆动时悬线上拉力的大小随时间变化的曲线如图所示。某同学由此图像提供的信息做出的下列判断中,正确的是( )
A.t=0.2 s时摆球正经过最低点
B.t=1.1 s时摆球正经过最低点
C.摆球摆动过程中机械能减小
D.摆球摆动的周期是T=1.4 s
解析 t=0.2 s时F最大,摆球速度最大正经过最低点,A正确;t=1.1 s时F最小,摆球在最高点,B错误;摆球经过最低点时的拉力越来越小,速度越来越小,则机械能逐渐减小,C正确;在一个周期内摆球两次经过最低点,由图像知周期T=1.2 s,D错误。
答案 AC
核心要点
受迫振动
如图所示的实验装置为一挂在曲轴上的弹簧振子,匀速摇动手柄,下面的弹簧振子就会振动起来。实际动手做一下,然后回答以下几个问题。
(1)如果手柄不动而用手拉动一下振子,从振幅角度看弹簧振子的振动属于什么振动?
(2)从没有系统外力作用角度看弹簧振子的振动属于什么振动?
(3)匀速摇动手柄时,观察到振幅有什么变化?为什么?
[观察探究]
(4)用不同的转速匀速转动手柄,弹簧振子的振动有何不同?这能说明什么问题?
答案 (1)阻尼振动 (2)固有振动 (3)振幅不变,提供系统外力,补偿系统损失的能量 (4)转速大时弹簧振子振动得快。说明弹簧振子振动的周期和频率由手柄转速决定。
[探究归纳]
简谐运动、阻尼振动和受迫振动的比较
振动类型
比较项目
简谐运动
阻尼振动
受迫振动
产生条件
不受阻力作用
受阻力作用
受阻力和驱动力作用
频率
固有频率
固有频率
驱动力频率
振幅
不变
减小
大小变化不确定
振动图像
形状不确定
实例
弹簧振子振动,单摆做小角度摆动
敲锣打鼓发出的声音越来越弱,是因为振幅越来越小
扬声器纸盆振动发声,钟摆的摆动
[例2] 如图所示,曲轴上悬挂一弹簧振子,转动摇把,曲轴可以带动弹簧振子上下振动。开始时不转动摇把,而让振子自由上下振动,测得其频率为2 Hz,然后匀速转动摇把,转速为240 r/min,当振子振动稳定时,它振动的周期为( )
A.0.5 s B.0.25 s C.2 s D.4 s
[试题案例]
答案 B
方法凝炼 求振动频率的步骤
解题步骤
解题注意事项
第一步:判断物体是做受迫振动还是固有振动
若物体是在周期性的驱动力作用下的振动则为受迫振动
第二步:区分物体的固有频率与驱动力的频率
做受迫振动的物体振动频率等于驱动力的频率
[针对训练2] (多选)某振动系统的固有频率为f0,在周期性驱动力的作用下做受迫振动,驱动力的频率为f。若驱动力的振幅保持不变,下列说法正确的是( )
A.当f<f0时,该振动系统的振幅随f增大而减小
B.当f>f0时,该振动系统的振幅随f减小而增大
C.该振动系统的振动稳定后,振动的频率等于f0
D.该振动系统的振动稳定后,振动的频率等于f
解析 物体在外界驱动力作用下的振动叫作受迫振动,物体做受迫振动时,振动稳定后的频率等于驱动力的频率,跟物体的固有频率没有关系,驱动力的频率接近物体的固有频率时,受迫振动的振幅增大,所以选项B、D正确,A、C错误。
答案 BD
核心要点
共 振
f驱=f固,即驱动力的频率等于振动系统的固有频率。
[要点归纳]
1.发生共振的条件
2.共振曲线:如图所示。
当驱动力的频率与物体的固有频率相等时,受迫振动的振幅最大。
3.对共振条件的理解
(1)从受力角度看:当振动物体所受驱动力的方向跟它的运动方向相同时,驱动力对它起加速作用,使它的振幅增大,当驱动力的频率等于物体的固有频率时,它的每一次作用都使物体的振幅增加,从而振幅达到最大。
(2)从功能关系看:当驱动力的频率等于物体的固有频率时,驱动力始终对物体做正功,使振动能量不断增加,振幅不断增大,直到增加的能量等于克服阻尼作用损耗的能量,振幅才不再增加。
[试题案例]
[例3] 如图所示是探究单摆共振条件时得到的图像,它表示振幅跟驱动力频率之间的关系,(g取9.8 m/s2)这个单摆的摆长是多少?
思维导图
答案 2.76 m
解析 从共振曲线知,单摆的固有周期
方法凝炼 共振问题的处理方法
(1)在分析解答有关共振问题时,要抓住产生共振的条件,驱动力的频率等于固有频率时产生共振,此时振动的振幅最大。
(2)在解决有关共振的实际问题时,要抽象出受迫振动这一物理模型,弄清驱动力频率和固有频率,然后利用共振的条件求解。
[针对训练3] (多选)如图为单摆在两次受迫振动中的共振曲线,则下列说法正确的是( )
A.若两次受迫振动分别在月球上和地球上进行,且摆长相同,则图线Ⅰ表示月球上单摆的共振曲线
B.若两次受迫振动是在地球上同一地点进行,则两次摆长之比lⅠ∶lⅡ=25∶4
C.图线Ⅱ若是在地面上完成的,则该摆摆长约为1 m
D.若摆长均为1 m,则图线Ⅰ是在地面上完成的
答案 ABC
核心素养
物理观念
科学思维
1.了解受迫振动、阻尼振动、固有频率的概念。
2.掌握受迫振动的频率由驱动力的频率决定。
3.知道共振发生的条件以及应用共振和防止共振的事例与方法。
观察演示实验,明确受迫振动的频率决定于驱动力的频率。
知识点一 振动中的能量损失
[观图助学]
生活中会见到阵风吹过树枝,使树枝左右摇摆,一会儿树枝就会停下来。而荡秋千的小朋友如无外界的帮助也会逐渐停下来。
(1)树枝的运动是什么运动?
(2)秋千的摆动是什么运动?
答案 (1)阻尼振动 (2)阻尼振动
1.固有振动和固有频率
如果振动系统没有______干预,此时的振动叫作固有振动,其振动频率称为__________。
2.阻尼振动
实际的振动系统都会受到摩擦、黏滞力等______作用,______必然逐渐减小,这种______随时间逐渐减小的振动,称为阻尼振动。
外力
固有频率
阻碍
振幅
振幅
1.驱动力
如果存在阻尼作用,振动系统最终会停止振动。为了使系统持续振动下去,对振动系统施加的周期性的______,外力对系统______,______系统的能量损耗,这种________的外力叫作驱动力。
2.受迫振动
(1)定义:系统在________作用下的振动,叫作受迫振动。
(2)受迫振动的频率(周期)
做受迫振动的物体,其振动频率总等于________的频率,与物体的__________无关。
知识点二 受迫振动
外力
做功
补偿
周期性
驱动力
驱动力
固有频率
知识点三 共振现象及其应用
[观图助学]
如图所示,先让A摆振动起来,A会通过张紧的绳子给其他各摆施加驱动力,B、C、D三个摆在驱动力作用下开始摆动:
(1)B、C、D三摆的频率有什么关系?
(2)观察B、C、D三摆的振幅,哪一个摆的振幅最大?摆的振幅与固有频率有什么关系。
提示 (1)B、C、D三摆都在做受迫振动,其频率都等于A摆的频率。
(2)B摆的振幅最大;在B、C、D三个摆中,A摆和B摆的摆长相等,故A摆的固有频率等于B摆的固有频率,由实验现象可知当A摆施加的驱动力的频率等于B摆的固有频率时,B摆的振幅最大。即受迫振动摆的振幅与本身固有频率和驱动力频率有关,固有频率越接近驱动力频率,受迫振动摆的振幅越大。
1.共振
驱动力频率f ______系统的固有频率f0时,受迫振动的______最大,这种现象叫作共振。
2.共振曲线(如图所示)
等于
振幅
3.共振的防止与利用
(1)利用:由共振的条件知,要利用共振,就应尽量使驱动力的频率与物体的固有频率一致。如共振筛、荡秋千、共振转速计等。
(2)防止:由共振曲线可知,在需要防止共振危害时,要尽量使驱动力的频率和固有频率不相等,而且相差越多越好。如:部队过桥应便步走。
说明:共振是物体做受迫振动时的一种特殊现象。
[思考判断]
(1)受迫振动的频率与振动系统的固有频率无关。( )
(2)驱动力频率越大,振幅越大。 ( )
(3)共振只有害处没有好处。( )
(4)做受迫振动的物体一定会发生共振。( )
(5)阻尼振动的频率随振幅的减小而不断减小。( )
√
×
×
×
×
1.同一简谐运动能量的大小由振幅大小确定,阻尼振动振幅减小的快慢跟所受阻尼的大小有关,阻尼越大,振幅减小得越快。
2.物体做阻尼振动时,振动的频率仍由自身结构特点所决定,并不会随振幅的减小而变化。例如用力敲锣,由于锣受到空气的阻尼作用,振幅越来越小,锣声减弱,但音调不变。
[要点归纳]
核心要点
阻尼振动
[试题案例]
[例1] (多选)一单摆在空气中振动,振幅逐渐减小,下列说法正确的是( )
A.单摆的机械能逐渐转化为其他形式的能
B.单摆后一时刻的动能一定小于前一时刻的动能
C.单摆振幅减小,频率也随着减小
D.单摆振幅虽然减小,但其频率不变
解析 单摆做阻尼振动,因不断克服空气阻力做功使机械能转化为其他形式的能,但是在振动过程中,动能和势能仍不断相互转化,单摆在从最大位移处向平衡位置运动的过程中,后一时刻的动能大于前一时刻的动能,故选项A正确,B错误;做阻尼振动的物体,频率由系统的特征决定,与振幅无关,所以其频率不变,选项C错误,D正确。
答案 AD
方法凝炼
理解阻尼振动要从两个方面入手:一是从振动能量上来讲,由于阻力做功,振动物体的机械能逐渐减小,振幅逐渐变小,但由于振动中动能与势能相互转化,不能说下一时刻的动能(或势能)变小;二是从振动周期、频率上看,周期与频率由振动系统本身决定,阻尼振动中周期、频率不变。
[针对训练1] (多选)将一个电动传感器接到计算机上,就可以测量快速变化的力,用这种方法测得的某单摆摆动时悬线上拉力的大小随时间变化的曲线如图所示。某同学由此图像提供的信息做出的下列判断中,正确的是( )
A.t=0.2 s时摆球正经过最低点
B.t=1.1 s时摆球正经过最低点
C.摆球摆动过程中机械能减小
D.摆球摆动的周期是T=1.4 s
解析 t=0.2 s时F最大,摆球速度最大正经过最低点,A正确;t=1.1 s时F最小,摆球在最高点,B错误;摆球经过最低点时的拉力越来越小,速度越来越小,则机械能逐渐减小,C正确;在一个周期内摆球两次经过最低点,由图像知周期T=1.2 s,D错误。
答案 AC
核心要点
受迫振动
如图所示的实验装置为一挂在曲轴上的弹簧振子,匀速摇动手柄,下面的弹簧振子就会振动起来。实际动手做一下,然后回答以下几个问题。
(1)如果手柄不动而用手拉动一下振子,从振幅角度看弹簧振子的振动属于什么振动?
(2)从没有系统外力作用角度看弹簧振子的振动属于什么振动?
(3)匀速摇动手柄时,观察到振幅有什么变化?为什么?
[观察探究]
(4)用不同的转速匀速转动手柄,弹簧振子的振动有何不同?这能说明什么问题?
答案 (1)阻尼振动 (2)固有振动 (3)振幅不变,提供系统外力,补偿系统损失的能量 (4)转速大时弹簧振子振动得快。说明弹簧振子振动的周期和频率由手柄转速决定。
[探究归纳]
简谐运动、阻尼振动和受迫振动的比较
振动类型
比较项目
简谐运动
阻尼振动
受迫振动
产生条件
不受阻力作用
受阻力作用
受阻力和驱动力作用
频率
固有频率
固有频率
驱动力频率
振幅
不变
减小
大小变化不确定
振动图像
形状不确定
实例
弹簧振子振动,单摆做小角度摆动
敲锣打鼓发出的声音越来越弱,是因为振幅越来越小
扬声器纸盆振动发声,钟摆的摆动
[例2] 如图所示,曲轴上悬挂一弹簧振子,转动摇把,曲轴可以带动弹簧振子上下振动。开始时不转动摇把,而让振子自由上下振动,测得其频率为2 Hz,然后匀速转动摇把,转速为240 r/min,当振子振动稳定时,它振动的周期为( )
A.0.5 s B.0.25 s C.2 s D.4 s
[试题案例]
答案 B
方法凝炼 求振动频率的步骤
解题步骤
解题注意事项
第一步:判断物体是做受迫振动还是固有振动
若物体是在周期性的驱动力作用下的振动则为受迫振动
第二步:区分物体的固有频率与驱动力的频率
做受迫振动的物体振动频率等于驱动力的频率
[针对训练2] (多选)某振动系统的固有频率为f0,在周期性驱动力的作用下做受迫振动,驱动力的频率为f。若驱动力的振幅保持不变,下列说法正确的是( )
A.当f<f0时,该振动系统的振幅随f增大而减小
B.当f>f0时,该振动系统的振幅随f减小而增大
C.该振动系统的振动稳定后,振动的频率等于f0
D.该振动系统的振动稳定后,振动的频率等于f
解析 物体在外界驱动力作用下的振动叫作受迫振动,物体做受迫振动时,振动稳定后的频率等于驱动力的频率,跟物体的固有频率没有关系,驱动力的频率接近物体的固有频率时,受迫振动的振幅增大,所以选项B、D正确,A、C错误。
答案 BD
核心要点
共 振
f驱=f固,即驱动力的频率等于振动系统的固有频率。
[要点归纳]
1.发生共振的条件
2.共振曲线:如图所示。
当驱动力的频率与物体的固有频率相等时,受迫振动的振幅最大。
3.对共振条件的理解
(1)从受力角度看:当振动物体所受驱动力的方向跟它的运动方向相同时,驱动力对它起加速作用,使它的振幅增大,当驱动力的频率等于物体的固有频率时,它的每一次作用都使物体的振幅增加,从而振幅达到最大。
(2)从功能关系看:当驱动力的频率等于物体的固有频率时,驱动力始终对物体做正功,使振动能量不断增加,振幅不断增大,直到增加的能量等于克服阻尼作用损耗的能量,振幅才不再增加。
[试题案例]
[例3] 如图所示是探究单摆共振条件时得到的图像,它表示振幅跟驱动力频率之间的关系,(g取9.8 m/s2)这个单摆的摆长是多少?
思维导图
答案 2.76 m
解析 从共振曲线知,单摆的固有周期
方法凝炼 共振问题的处理方法
(1)在分析解答有关共振问题时,要抓住产生共振的条件,驱动力的频率等于固有频率时产生共振,此时振动的振幅最大。
(2)在解决有关共振的实际问题时,要抽象出受迫振动这一物理模型,弄清驱动力频率和固有频率,然后利用共振的条件求解。
[针对训练3] (多选)如图为单摆在两次受迫振动中的共振曲线,则下列说法正确的是( )
A.若两次受迫振动分别在月球上和地球上进行,且摆长相同,则图线Ⅰ表示月球上单摆的共振曲线
B.若两次受迫振动是在地球上同一地点进行,则两次摆长之比lⅠ∶lⅡ=25∶4
C.图线Ⅱ若是在地面上完成的,则该摆摆长约为1 m
D.若摆长均为1 m,则图线Ⅰ是在地面上完成的
答案 ABC
