人教版(2019)高中物理 选择性必修第一册 第2章 章末总结课件
文档属性
| 名称 | 人教版(2019)高中物理 选择性必修第一册 第2章 章末总结课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-08 14:41:58 | ||
图片预览











文档简介
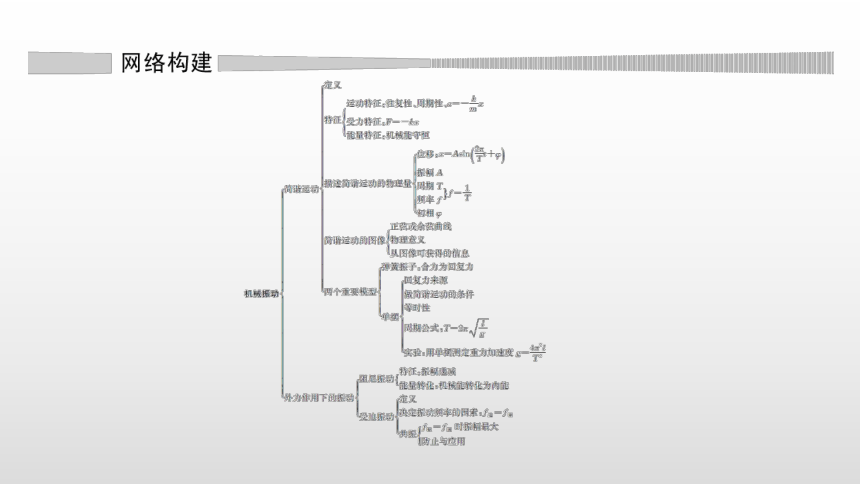
章末总结
突破一 简谐运动的图像及应用
(1)可以确定振动物体在任一时刻的位移。如图所示,对应t1、t2时刻的位移分别为x1=7 cm,x2=-5 cm。
(2)确定振动的振幅。图中最大位移的大小就是振幅,如图表示振动的振幅是10 cm。
[例1] 如图所示是一个质点做简谐运动的图像,根据图像回答下面的问题:
(1)振动质点离开平衡位置的最大距离;
(2)写出此振动质点的运动表达式;
(3)振动质点在0~0.6 s的时间内通过的路程;
(4)振动质点在t=0.1 s、0.3 s、0.5 s、0.7 s时的振动方向;
(5)振动质点在0.6~0.8 s这段时间内速度和加速度是怎样变化的?
(6)振动质点在0.4~0.8 s这段时间内的动能变化是多少?
解析 (1)由振动图像可以看出,质点振动的振幅为5 cm,即此质点离开平衡位置的最大距离。
(4)在t=0.1 s时,振动质点处在位移为正值的某一位置上,但若从t=0.1 s起取一段极短的时间间隔Δt(Δt→0)的话,从图像中可以看出振动质点的正方向的位移将会越来越大,由此可以判断得出质点在t=0.1 s时的振动方向是沿题中所设的正方向。同理可以判断得出质点在t=0.3 s、0.5 s、0.7 s时的振动方向分别是沿题中所设的负方向、负方向和正方向。
(5)由振动图像可以看出,在0.6~0.8 s这段时间内,振动质点从最大位移处向平衡位置运动,故其速度是越来越大的;而质点所受的回复力是指向平衡位置的,并且逐渐减小的,故其加速度的方向指向平衡位置且越来越小。
(6)由图像可看出,在0.4~0.8 s这段时间内质点从平衡位置经过半个周期的运动又回到了平衡位置,尽管初、末两个时刻的速度方向相反,但大小是相等的,故这段时间内质点的动能变化为零。
答案 见解析
[针对训练1] (多选)一质点做简谐运动的图像如图所示,则该质点( )
A.在0.015 s时,速度和加速度都为x轴负方向
B.在0.01 s至0.03 s内,速度与加速度先反方向后同方向,且速度是先减小后增大,加速度是先增大后减小
C.在第八个0.01 s内,速度与位移方向相同,且都在不断增大
D.在1 s内,回复力的瞬时功率有100次为零
答案 BD
突破二 简谐运动的周期性和对称性
1.周期性:做简谐运动的物体在完成一次全振动后,再次振动时则是重复上—个全振动的形式,所以做简谐运动的物体经过同一位置可以对应不同的时刻,做简谐运动的物体具有周期性。
2.对称性
(1)速率的对称性:系统在关于平衡位置对称的两位置具有相等的速率。
(2)加速度和回复力的对称性:系统在关于平衡位置对称的两位置具有等大反向的加速度和回复力。
(3)时间的对称性:系统通过关于平衡位置对称的两段位移的时间相等,振动过程中通过任意两点A、B的时间与逆向通过的时间相等。
[例2] 弹簧振子以O点为平衡位置,在B、C两点间做简谐运动,在t=0时刻,从O、B间的P点以速度v向B点运动;在t=0.20 s时,振子速度第一次变为-v;再经过0.30 s时,振子速度第二次变为-v。
(1)求弹簧振子振动的周期T;
(2)若B、C之间的距离为25 cm,求振子在4.0 s内通过的路程。
思路引导 将物理过程模型化,画具体的图景,根据简谐运动的周期性和对称性分析求解。
(2)振子的振幅A=12.5 cm,因t=4T,所以振子通过的路程s=4×4A=200 cm。
答案 (1)1.00 s (2)200 cm
方法凝炼
求解该类题目的关键是弄清物理的情景,画出振子的物理过程图示,结合简谐运动的对称性及周期性分析讨论。
[针对训练2] (2018·天津理综)(多选)一振子沿x轴做简谐运动,平衡位置在坐标原点。t=0时振子的位移为-0.1 m,t=1 s时位移为0.1 m,则( )
答案 AD
突破三 解决简谐运动的物理思想方法
1.理想模型法
弹簧振子是一种理想化模型,它忽略了弹簧的质量及摩擦力和空气阻力。单摆是实际摆的理想化模型,忽略了绳的质量、粗细、伸缩及球的大小、空气阻力等。这种理想化的近似可以使问题大为简化,有利于对物理现象和物理规律的探究和认识。
2.图像法
图像法是物理学中常用的一种思维方法,它能够形象直观地反映物理规律,帮助我们认识物理现象和解决物理问题。用图像法研究物体的振动时,应注意物体振动的周期、振幅、相位等。
3.等效法
本章有两个重要的物理模型,分别是弹簧振子模型和单摆模型。凡是具有与它们相同运动规律的系统都可以等效为弹簧振子模型或单摆模型,可以用弹簧振子或单摆的有关知识分析。
4.对称法
由于简谐运动具有周期性和对称性,我们可以根据已知的一部分运动情况分析出其他阶段的运动情况。
答案 C
[例4] 如图(a)所示,一只昆虫水平飞向一个原来静止悬挂的单摆,并抱住摆球,结果单摆做简谐运动,其振动图像如图(b)所示,已知摆球的质量是昆虫的5倍,求昆虫飞来时速度的大小。(取g=10 m/s2)
解析 设昆虫的质量为m,飞来的速度为v0,
单摆运动在平衡位置时的速度为v,
由动量守恒定律有mv0=(m+5m)v
设摆球摆动的最大高度为h(如图所示),
根据机械能守恒定律有
由题图(b)可知,单摆运动的振幅为A=a=0.1 m,周期为T=4 s,
答案 0.94 m/s
[针对训练3] 如图所示,处于竖直向下的匀强电场中的摆球,质量为m,半径为r,带正电荷,用长为L的细线把摆球吊在悬点O处做成单摆,则这个单摆的周期为( )
答案 D
突破四 简谐运动与其他运动的综合
简谐运动是不同于匀速直线运动、匀变速直线运动以及匀速圆周运动的一种特殊运动,它有自己的特点,如周期性、对称性,这些在与其他运动综合考查的过程中要特别注意。
找出运动之间的联系是解题的关键,但对每种运动来说又是独立的。简谐运动具有周期性,但是否考虑其周期性要由题目需要来决定。
答案 BC
[针对训练4] 将一测力传感器连接到计算机上就可以测量快速变化的力。如图甲表示小滑块(可视为质点)沿固定的光滑半球形容器内壁在竖直平面的A、A′之间来回滑动。A、A′点与O点连线与竖直方向之间夹角θ相等且很小,图乙表示滑块对器壁的压力F随时间t变化的曲线,图中t=0为滑块从A点开始运动的时刻。试根据力学规律和题中(包括图中)所给的信息,g取10 m/s2。求:
(2)在最高点A有Fmin=mgcos θ
(1)容器的半径;
(2)小滑块的质量;
(3)滑块运动过程中的机械能。
答案 (1)0.1 m (2)0.05 kg (3)5×10-4 J
解得m=0.05 kg。
(3)滑块机械能守恒
突破一 简谐运动的图像及应用
(1)可以确定振动物体在任一时刻的位移。如图所示,对应t1、t2时刻的位移分别为x1=7 cm,x2=-5 cm。
(2)确定振动的振幅。图中最大位移的大小就是振幅,如图表示振动的振幅是10 cm。
[例1] 如图所示是一个质点做简谐运动的图像,根据图像回答下面的问题:
(1)振动质点离开平衡位置的最大距离;
(2)写出此振动质点的运动表达式;
(3)振动质点在0~0.6 s的时间内通过的路程;
(4)振动质点在t=0.1 s、0.3 s、0.5 s、0.7 s时的振动方向;
(5)振动质点在0.6~0.8 s这段时间内速度和加速度是怎样变化的?
(6)振动质点在0.4~0.8 s这段时间内的动能变化是多少?
解析 (1)由振动图像可以看出,质点振动的振幅为5 cm,即此质点离开平衡位置的最大距离。
(4)在t=0.1 s时,振动质点处在位移为正值的某一位置上,但若从t=0.1 s起取一段极短的时间间隔Δt(Δt→0)的话,从图像中可以看出振动质点的正方向的位移将会越来越大,由此可以判断得出质点在t=0.1 s时的振动方向是沿题中所设的正方向。同理可以判断得出质点在t=0.3 s、0.5 s、0.7 s时的振动方向分别是沿题中所设的负方向、负方向和正方向。
(5)由振动图像可以看出,在0.6~0.8 s这段时间内,振动质点从最大位移处向平衡位置运动,故其速度是越来越大的;而质点所受的回复力是指向平衡位置的,并且逐渐减小的,故其加速度的方向指向平衡位置且越来越小。
(6)由图像可看出,在0.4~0.8 s这段时间内质点从平衡位置经过半个周期的运动又回到了平衡位置,尽管初、末两个时刻的速度方向相反,但大小是相等的,故这段时间内质点的动能变化为零。
答案 见解析
[针对训练1] (多选)一质点做简谐运动的图像如图所示,则该质点( )
A.在0.015 s时,速度和加速度都为x轴负方向
B.在0.01 s至0.03 s内,速度与加速度先反方向后同方向,且速度是先减小后增大,加速度是先增大后减小
C.在第八个0.01 s内,速度与位移方向相同,且都在不断增大
D.在1 s内,回复力的瞬时功率有100次为零
答案 BD
突破二 简谐运动的周期性和对称性
1.周期性:做简谐运动的物体在完成一次全振动后,再次振动时则是重复上—个全振动的形式,所以做简谐运动的物体经过同一位置可以对应不同的时刻,做简谐运动的物体具有周期性。
2.对称性
(1)速率的对称性:系统在关于平衡位置对称的两位置具有相等的速率。
(2)加速度和回复力的对称性:系统在关于平衡位置对称的两位置具有等大反向的加速度和回复力。
(3)时间的对称性:系统通过关于平衡位置对称的两段位移的时间相等,振动过程中通过任意两点A、B的时间与逆向通过的时间相等。
[例2] 弹簧振子以O点为平衡位置,在B、C两点间做简谐运动,在t=0时刻,从O、B间的P点以速度v向B点运动;在t=0.20 s时,振子速度第一次变为-v;再经过0.30 s时,振子速度第二次变为-v。
(1)求弹簧振子振动的周期T;
(2)若B、C之间的距离为25 cm,求振子在4.0 s内通过的路程。
思路引导 将物理过程模型化,画具体的图景,根据简谐运动的周期性和对称性分析求解。
(2)振子的振幅A=12.5 cm,因t=4T,所以振子通过的路程s=4×4A=200 cm。
答案 (1)1.00 s (2)200 cm
方法凝炼
求解该类题目的关键是弄清物理的情景,画出振子的物理过程图示,结合简谐运动的对称性及周期性分析讨论。
[针对训练2] (2018·天津理综)(多选)一振子沿x轴做简谐运动,平衡位置在坐标原点。t=0时振子的位移为-0.1 m,t=1 s时位移为0.1 m,则( )
答案 AD
突破三 解决简谐运动的物理思想方法
1.理想模型法
弹簧振子是一种理想化模型,它忽略了弹簧的质量及摩擦力和空气阻力。单摆是实际摆的理想化模型,忽略了绳的质量、粗细、伸缩及球的大小、空气阻力等。这种理想化的近似可以使问题大为简化,有利于对物理现象和物理规律的探究和认识。
2.图像法
图像法是物理学中常用的一种思维方法,它能够形象直观地反映物理规律,帮助我们认识物理现象和解决物理问题。用图像法研究物体的振动时,应注意物体振动的周期、振幅、相位等。
3.等效法
本章有两个重要的物理模型,分别是弹簧振子模型和单摆模型。凡是具有与它们相同运动规律的系统都可以等效为弹簧振子模型或单摆模型,可以用弹簧振子或单摆的有关知识分析。
4.对称法
由于简谐运动具有周期性和对称性,我们可以根据已知的一部分运动情况分析出其他阶段的运动情况。
答案 C
[例4] 如图(a)所示,一只昆虫水平飞向一个原来静止悬挂的单摆,并抱住摆球,结果单摆做简谐运动,其振动图像如图(b)所示,已知摆球的质量是昆虫的5倍,求昆虫飞来时速度的大小。(取g=10 m/s2)
解析 设昆虫的质量为m,飞来的速度为v0,
单摆运动在平衡位置时的速度为v,
由动量守恒定律有mv0=(m+5m)v
设摆球摆动的最大高度为h(如图所示),
根据机械能守恒定律有
由题图(b)可知,单摆运动的振幅为A=a=0.1 m,周期为T=4 s,
答案 0.94 m/s
[针对训练3] 如图所示,处于竖直向下的匀强电场中的摆球,质量为m,半径为r,带正电荷,用长为L的细线把摆球吊在悬点O处做成单摆,则这个单摆的周期为( )
答案 D
突破四 简谐运动与其他运动的综合
简谐运动是不同于匀速直线运动、匀变速直线运动以及匀速圆周运动的一种特殊运动,它有自己的特点,如周期性、对称性,这些在与其他运动综合考查的过程中要特别注意。
找出运动之间的联系是解题的关键,但对每种运动来说又是独立的。简谐运动具有周期性,但是否考虑其周期性要由题目需要来决定。
答案 BC
[针对训练4] 将一测力传感器连接到计算机上就可以测量快速变化的力。如图甲表示小滑块(可视为质点)沿固定的光滑半球形容器内壁在竖直平面的A、A′之间来回滑动。A、A′点与O点连线与竖直方向之间夹角θ相等且很小,图乙表示滑块对器壁的压力F随时间t变化的曲线,图中t=0为滑块从A点开始运动的时刻。试根据力学规律和题中(包括图中)所给的信息,g取10 m/s2。求:
(2)在最高点A有Fmin=mgcos θ
(1)容器的半径;
(2)小滑块的质量;
(3)滑块运动过程中的机械能。
答案 (1)0.1 m (2)0.05 kg (3)5×10-4 J
解得m=0.05 kg。
(3)滑块机械能守恒
