三角形全等的判定(SSS)
文档属性
| 名称 | 三角形全等的判定(SSS) |  | |
| 格式 | zip | ||
| 文件大小 | 83.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-23 21:46:23 | ||
图片预览

文档简介
11.2 三角形全等的判定
第1课时 三角形全等的判定(SSS)
【要点归纳】
1.三角形全等的判定
如果两个三角形满足三条边对应相等,三个角对应相等,那么它们全等。
如果两个三角形满足三边三角六个条件中的一个或者两个对应相等,那么不能保证三角形全等。
两个三角形全等至少需要三个条件对应相等。
2.三角形全等的“SSS”判定方法 三边对应相等的两个三角形全等(可以简写成“边边边”或者“SSS”)
【题型归类】
类型一:利用“SSS”证明三角形全等
例1. 如图11-2-1。已知AB=AC,AE=AD,BD=CE,求证:△AEB≌△ADC.
【点拨】此题考查三角形全等条件SSS的应用.在确定的两个三角形中找全等的条件是证明三角形全等的常用方法.要证明△AEB≌△ADC,已经具备了两个条件AB=AC,AE=AD.第三个条件BE=CD需要由BD=CE得出.
【证明】∵BD=CE,
∴BD-ED=CE-ED,即BE=CD,
在△AEB和△ADC中,
∴△AEB≌△ADC(SSS)
类型二:利用三角形全等证明线段(或者角)相等,直线平行
例2.如图11-2-2所示,AB=CD,AE=DF,CE=BF,判断EC与BF的数量和位置关系,说明理由。
【点拨】此题综合考查全等三角形的判定和性质。要说明EC∥BF,只要∠ACE=∠DBF ,进而考虑证明△AEC≌△DFB 。
【解】 EC∥BF,EC=BF。
理由:∵AB=CD,
∴AB+BC=CD+BC,
即AC=DB
在△ACE和△DBFC中
∴△ACE≌△DBFC(SSS)
∴∠ACE=∠DBF,EC=BF。
∴EC∥BF。
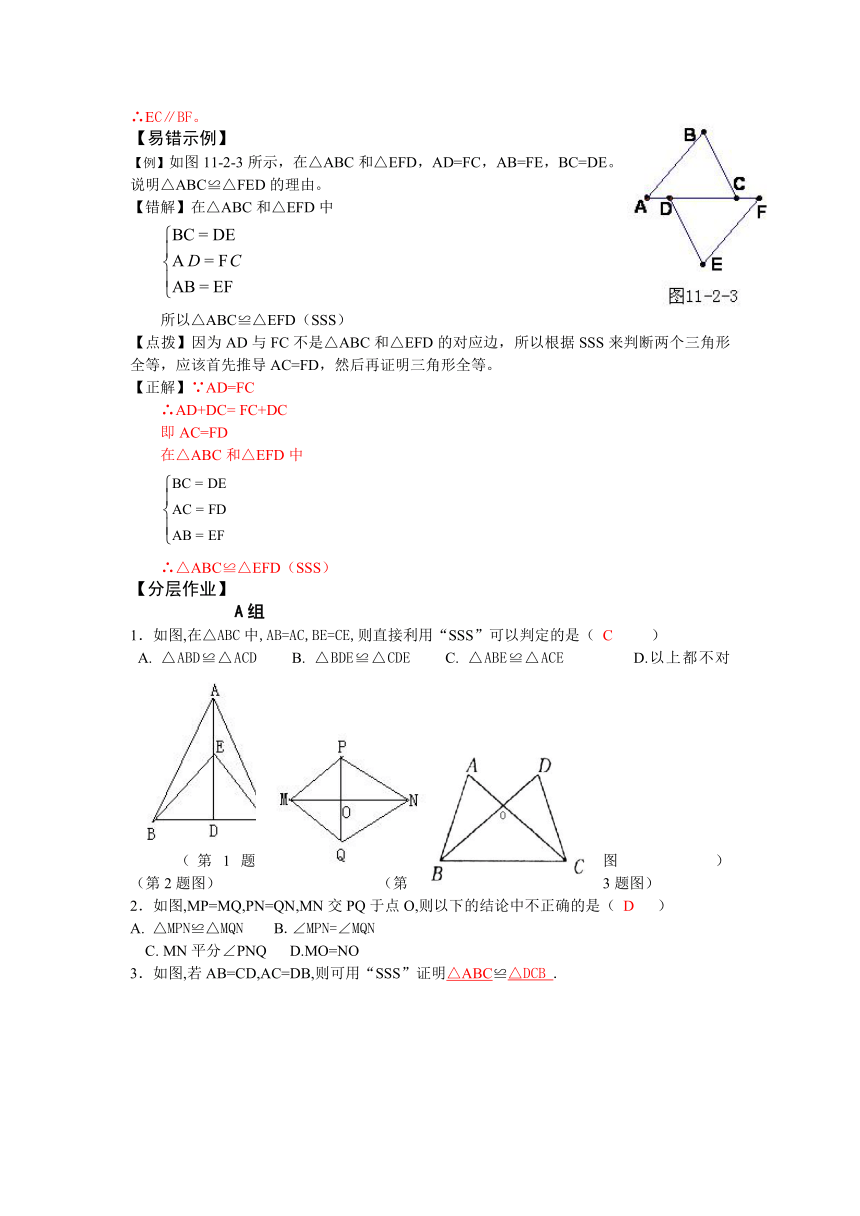
【易错示例】
【例】如图11-2-3所示,在△ABC和△EFD,AD=FC,AB=FE,BC=DE。说明△ABC≌△FED的理由。
【错解】在△ABC和△EFD中
所以△ABC≌△EFD(SSS)
【点拨】因为AD与FC不是△ABC和△EFD的对应边,所以根据SSS来判断两个三角形全等,应该首先推导AC=FD,然后再证明三角形全等。
【正解】∵AD=FC
∴AD+DC= FC+DC
即AC=FD
在△ABC和△EFD中
∴△ABC≌△EFD(SSS)
【分层作业】
A组
1.如图,在△ABC中,AB=AC,BE=CE,则直接利用“SSS”可以判定的是( C )
A. △ABD≌△ACD B. △BDE≌△CDE C. △ABE≌△ACE D.以上都不对
(第1题图 ) (第2题图) (第3题图)
2.如图,MP=MQ,PN=QN,MN交PQ于点O,则以下的结论中不正确的是( D )
A. △MPN≌△MQN B.∠MPN=∠MQN
C. MN平分∠PNQ D.MO=NO
3.如图,若AB=CD,AC=DB,则可用“SSS”证明△ABC≌△DCB .
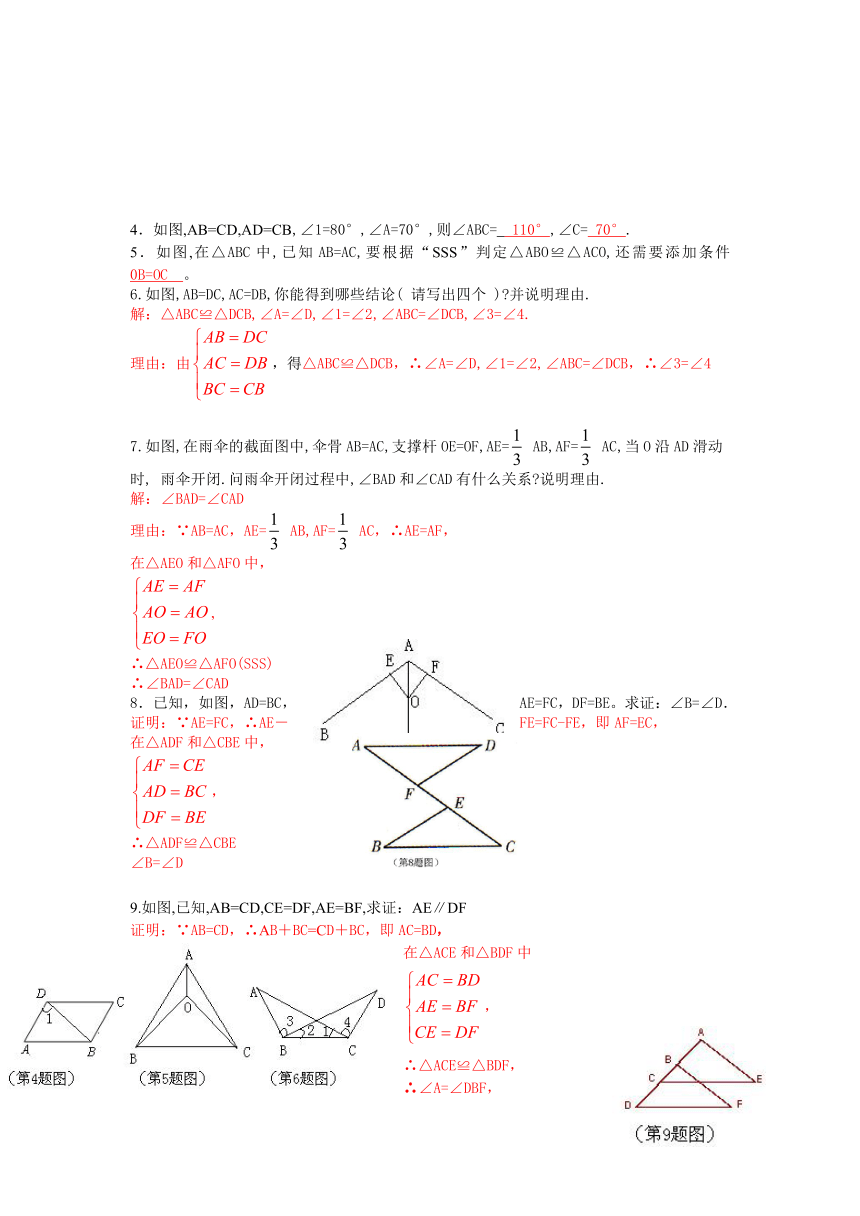
4.如图,AB=CD,AD=CB,∠1=80°,∠A=70°,则∠ABC= 110°,∠C= 70°.
5.如图,在△ABC中,已知AB=AC,要根据“SSS”判定△ABO≌△ACO,还需要添加条件 0B=OC 。
6.如图,AB=DC,AC=DB,你能得到哪些结论( 请写出四个 ) 并说明理由.
解:△ABC≌△DCB,∠A=∠D,∠1=∠2,∠ABC=∠DCB,∠3=∠4.
理由:由,得△ABC≌△DCB,∴∠A=∠D,∠1=∠2,∠ABC=∠DCB,∴∠3=∠4
7.如图,在雨伞的截面图中,伞骨AB=AC,支撑杆OE=OF,AE= AB,AF= AC,当O沿AD滑动时, 雨伞开闭.问雨伞开闭过程中,∠BAD和∠CAD有什么关系 说明理由.
解:∠BAD=∠CAD
理由:∵AB=AC,AE= AB,AF= AC,∴AE=AF,
在△AEO和△AFO中,
,
∴△AEO≌△AFO(SSS)
∴∠BAD=∠CAD
8.已知,如图,AD=BC,AE=FC,DF=BE。求证:∠B=∠D.
证明:∵AE=FC,∴AE-FE=FC-FE,即AF=EC,
在△ADF和△CBE中,
,
∴△ADF≌△CBE
∠B=∠D
9.如图,已知,AB=CD,CE=DF,AE=BF,求证:AE∥DF
证明:∵AB=CD,∴AB+BC=CD+BC,即AC=BD,
在△ACE和△BDF中
,
∴△ACE≌△BDF,
∴∠A=∠DBF,
∴AE∥DF
B组
10.如图在四边形ABCD中,AB=CD,AD=CB,
(1)AD与BC有怎样的位置关系 请说明理由;
(2)∠B与∠D相等吗 为什么
解:(1)AD∥BC,理由略。
(2)∠B=∠D,理由略。
11.如图,△ABE≌△ACD,求证:∠1=∠2
证明:∵△ABE≌△ACD,
∴AB=AC,AE=AD,BE=CD,
∴AB-AD=AC-AE,即DB=EC,
在△DEB和△EDC中
∴△DEB≌△EDC(SSS)。
∴∠1=∠2。
第1课时 三角形全等的判定(SSS)
【要点归纳】
1.三角形全等的判定
如果两个三角形满足三条边对应相等,三个角对应相等,那么它们全等。
如果两个三角形满足三边三角六个条件中的一个或者两个对应相等,那么不能保证三角形全等。
两个三角形全等至少需要三个条件对应相等。
2.三角形全等的“SSS”判定方法 三边对应相等的两个三角形全等(可以简写成“边边边”或者“SSS”)
【题型归类】
类型一:利用“SSS”证明三角形全等
例1. 如图11-2-1。已知AB=AC,AE=AD,BD=CE,求证:△AEB≌△ADC.
【点拨】此题考查三角形全等条件SSS的应用.在确定的两个三角形中找全等的条件是证明三角形全等的常用方法.要证明△AEB≌△ADC,已经具备了两个条件AB=AC,AE=AD.第三个条件BE=CD需要由BD=CE得出.
【证明】∵BD=CE,
∴BD-ED=CE-ED,即BE=CD,
在△AEB和△ADC中,
∴△AEB≌△ADC(SSS)
类型二:利用三角形全等证明线段(或者角)相等,直线平行
例2.如图11-2-2所示,AB=CD,AE=DF,CE=BF,判断EC与BF的数量和位置关系,说明理由。
【点拨】此题综合考查全等三角形的判定和性质。要说明EC∥BF,只要∠ACE=∠DBF ,进而考虑证明△AEC≌△DFB 。
【解】 EC∥BF,EC=BF。
理由:∵AB=CD,
∴AB+BC=CD+BC,
即AC=DB
在△ACE和△DBFC中
∴△ACE≌△DBFC(SSS)
∴∠ACE=∠DBF,EC=BF。
∴EC∥BF。
【易错示例】
【例】如图11-2-3所示,在△ABC和△EFD,AD=FC,AB=FE,BC=DE。说明△ABC≌△FED的理由。
【错解】在△ABC和△EFD中
所以△ABC≌△EFD(SSS)
【点拨】因为AD与FC不是△ABC和△EFD的对应边,所以根据SSS来判断两个三角形全等,应该首先推导AC=FD,然后再证明三角形全等。
【正解】∵AD=FC
∴AD+DC= FC+DC
即AC=FD
在△ABC和△EFD中
∴△ABC≌△EFD(SSS)
【分层作业】
A组
1.如图,在△ABC中,AB=AC,BE=CE,则直接利用“SSS”可以判定的是( C )
A. △ABD≌△ACD B. △BDE≌△CDE C. △ABE≌△ACE D.以上都不对
(第1题图 ) (第2题图) (第3题图)
2.如图,MP=MQ,PN=QN,MN交PQ于点O,则以下的结论中不正确的是( D )
A. △MPN≌△MQN B.∠MPN=∠MQN
C. MN平分∠PNQ D.MO=NO
3.如图,若AB=CD,AC=DB,则可用“SSS”证明△ABC≌△DCB .
4.如图,AB=CD,AD=CB,∠1=80°,∠A=70°,则∠ABC= 110°,∠C= 70°.
5.如图,在△ABC中,已知AB=AC,要根据“SSS”判定△ABO≌△ACO,还需要添加条件 0B=OC 。
6.如图,AB=DC,AC=DB,你能得到哪些结论( 请写出四个 ) 并说明理由.
解:△ABC≌△DCB,∠A=∠D,∠1=∠2,∠ABC=∠DCB,∠3=∠4.
理由:由,得△ABC≌△DCB,∴∠A=∠D,∠1=∠2,∠ABC=∠DCB,∴∠3=∠4
7.如图,在雨伞的截面图中,伞骨AB=AC,支撑杆OE=OF,AE= AB,AF= AC,当O沿AD滑动时, 雨伞开闭.问雨伞开闭过程中,∠BAD和∠CAD有什么关系 说明理由.
解:∠BAD=∠CAD
理由:∵AB=AC,AE= AB,AF= AC,∴AE=AF,
在△AEO和△AFO中,
,
∴△AEO≌△AFO(SSS)
∴∠BAD=∠CAD
8.已知,如图,AD=BC,AE=FC,DF=BE。求证:∠B=∠D.
证明:∵AE=FC,∴AE-FE=FC-FE,即AF=EC,
在△ADF和△CBE中,
,
∴△ADF≌△CBE
∠B=∠D
9.如图,已知,AB=CD,CE=DF,AE=BF,求证:AE∥DF
证明:∵AB=CD,∴AB+BC=CD+BC,即AC=BD,
在△ACE和△BDF中
,
∴△ACE≌△BDF,
∴∠A=∠DBF,
∴AE∥DF
B组
10.如图在四边形ABCD中,AB=CD,AD=CB,
(1)AD与BC有怎样的位置关系 请说明理由;
(2)∠B与∠D相等吗 为什么
解:(1)AD∥BC,理由略。
(2)∠B=∠D,理由略。
11.如图,△ABE≌△ACD,求证:∠1=∠2
证明:∵△ABE≌△ACD,
∴AB=AC,AE=AD,BE=CD,
∴AB-AD=AC-AE,即DB=EC,
在△DEB和△EDC中
∴△DEB≌△EDC(SSS)。
∴∠1=∠2。
