人教版八年级上册数学:13.3.1 等腰三角形10道典型题 课件(共25张PPT)
文档属性
| 名称 | 人教版八年级上册数学:13.3.1 等腰三角形10道典型题 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 292.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 13:56:26 | ||
图片预览





文档简介
(共25张PPT)
本专题考察的知识点
1.等腰三角形的性质与应用
2.等边三角形的性质与应用
3.含30°直角三角形的性质
4.分类讨论的思想方法在等腰三角形中的应用
例1.
已知等腰三角形的一个角是70°,求其余两角.
思路分析:已知等腰三角形的一个角是70°,那么这个70°的角可能为等腰三角形的底角或为等腰三角形的顶角;由三角形内角和定理易求出其余两角.
70°、40°或55°、55°
;
引申:
已知等腰三角形的一个角是110°,求其余两角.
答案:其余两角为35°、35°.
归纳:等腰三角形的顶角可以是锐角、直角和钝角;
底角只能是锐角.所以,看到等腰三角形中的一个角的度数时,要注意判断这个角可能是顶角还是底角,是否需要分类讨论.
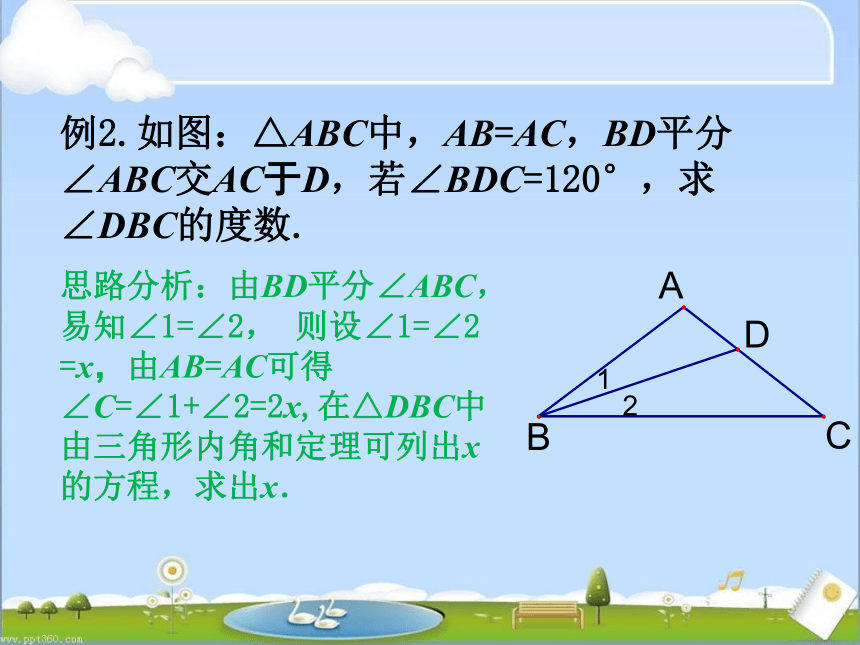
例2.如图:△ABC中,AB=AC,BD平分∠ABC交AC于D,若∠BDC=120°,求∠DBC的度数.
思路分析:由BD平分∠ABC,易知∠1=∠2,
则设∠1=∠2
=x,由AB=AC可得∠C=∠1+∠2=2x,在△DBC中由三角形内角和定理可列出x的方程,求出x.
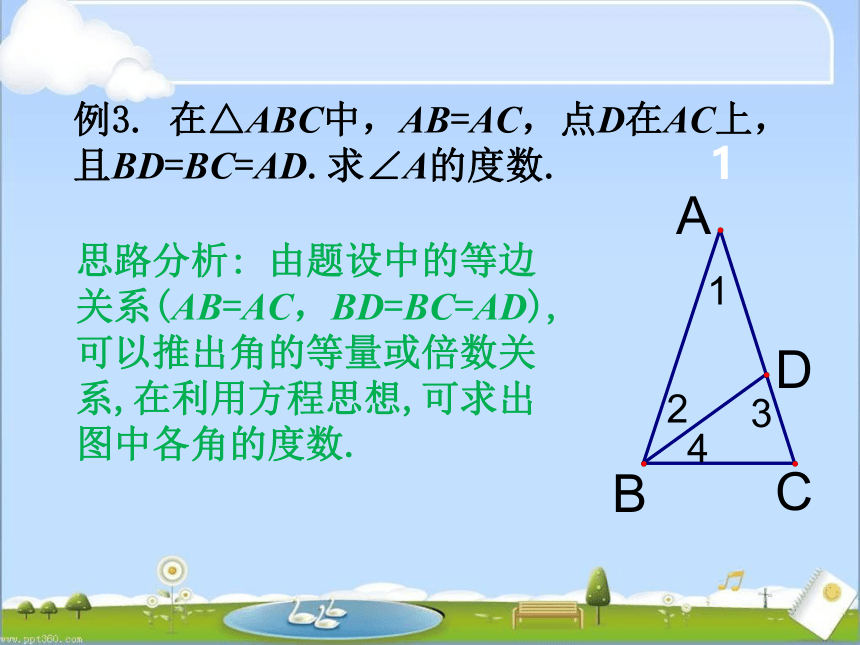
例3.
在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.求∠A的度数.
思路分析:
由题设中的等边关系(AB=AC,BD=BC=AD),可以推出角的等量或倍数关系,在利用方程思想,可求出图中各角的度数.
1
解:设∠1=x,∵BD=BC=AD
,
∴∠1=∠2,∠3=∠C,
∵∠3
=∠C=∠1+∠2=2x,
∵AB=AC,∴∠ABC=∠C=2x,
在△ABC中,∠A+∠ABC+∠C=180°,
即5x=180°,∴∠A=x=36°.
例4.
证明:等腰三角形底边中点到两腰的距离相等.
提示:
本题为文字命题,解题时应分为以下
三个步骤:
(1)根据题意作图;
(2)写出已知,
(3)进行求证.
例5.如图:在三角形ABC中,AB=AC,
BD⊥AC于D,求证:∠DBC=
∠A.
思路分析:由等腰三角形“三线合一”可联想到作底边的高,可推出1/2∠BAC=∠EAC,
由BD⊥AC,AE为高可知∠EAC和∠DBC都与∠C互余,推出∠DBC=∠EAC=1/2∠BAC.
E
E
证明:过点A作AE⊥BC于点E,
又∵AB=AC,
∴∠EAC
=1/2∠BAC,
∵BD⊥AC,AE为高可知,
∴∠EAC和∠DBC都与∠C互余,
∴∠DBC=∠EAC=1/2∠A
课间休息十分钟……
例6.在△ABC中,AB=AC,D是
CA延长线上一点,DF⊥BC于F,
交AB于E,求证:AE=AD.
思路分析:由等腰三角形“三线合一”可联想到作底边的高AM,可推出∠1=∠2,由DF⊥AC,AM⊥BC可知DF∥AM,从而∠3=∠4,证出结论.
M
1
3
4
2
3
4
1
2
证明:过点A作AM⊥BC于M,
∵AB=AC,
∴∠1=∠2,
∵DF⊥AC,AM⊥BC,
∴DF∥AM,
∴∠3=∠1,
∠2=∠4
∴∠3=∠4
,
∴AD=AE.
例7.如图,△ABC是正三角形,D、E、F分别是AB、BC、CA上的点,且AD=BE=CF,试说明△DEF是等边三角形.
思路分析:利用等边三角形的性质可推出,边、角的等量关系,从而易证三角形全等。进而说明△DEF是等边三角形.
证明:∵△ABC是正三角形,∴AB=BC=CA,∠A=∠B=∠C=60°,
又∵AD=BE=CF,
∴BD=EC=AF,
∴△ADF≌△BED≌△CFE,
∴DE=EF=DF
∴△DEF是等边三角形.
例8.如图,△ABD、
△AEC都是等边三角形,求证:
△AFG是等边三角形.
思路分析:利用等边三角形的性质可推出,边、角的等量关系,从而易证三角形全等,进而说明△AFG是等边三角形.
证明:∵△ABD
和△AED是正三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=60°,
∴
∠CAD=∠BAD+∠CAB=60°+∠CAB,
∠BAE=∠CAE+∠CAB=60°+∠CAB,
∴
∠CAD=∠BAE,
△ADC≌△BAE,
∴
∠ADF=∠GBA.
又∵AD=AB,
∠FAG=180°-∠BAD-∠CAE=60°,
∠FAG=∠DAF=60°,
∴△ADF≌△BAG,
∴AF=AG,
又∵∠FAG=60°,
∴△DEF是等边三角形.
例9.
求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
提示:本题为文字命题,首先应根据题意作图;写出已知,求证.
已知:∠CAE为△ABC的外角,∠1=∠2,
AD∥BC.求证:AB=AC
A
B
C
D
E
1
2
思路分析:欲证AB=AC
可
先证∠B=∠C,又∠1=∠2,所以应设法寻求∠B、∠C
与∠1、∠2的关系,又由
AD∥BC易得结论.
证明:
∵AD∥BC,
∴∠1=∠B(两直线平行,
同位角相等),
∠2=∠C(两直线平行,
内错角相等).
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等边对等角).
A
B
C
D
E
1
2
例10.已知:△ABC中,∠ABC=3∠C,
∠1=∠2,BE⊥AE.
求证:AC-AB=2BE.
思路分析:延长BE与AC交于点F,构造全等三角形∴△ABE≌△AFE,则2BE=BF,AC-AB=CF,我们只要判定△FBC为等腰三角形即可.
F
证明:延长BE与AC交于点F,
∵BE⊥AE.
∴∠AEB=∠AEF=90°
,
∵∠1=∠2,AE=AE,
∴△ABE≌△AFE,
∴2BE=BF,AB=AF,
∴AC-AB=AC-AF=FC,
∴∠ABF=∠AFB=∠FBC+∠C.
∵∠ABC=3∠C,
∴∠ABF+∠FBC=3∠C,
∴∠FBC+∠C+∠FBC=3∠C,
∴∠FBC=∠C,
∴BF=FC,
∴AC-AB=2BE.
本专题考察的知识点
1.等腰三角形的性质与应用
2.等边三角形的性质与应用
3.含30°直角三角形的性质
4.分类讨论的思想方法在等腰三角形中的应用
例1.
已知等腰三角形的一个角是70°,求其余两角.
思路分析:已知等腰三角形的一个角是70°,那么这个70°的角可能为等腰三角形的底角或为等腰三角形的顶角;由三角形内角和定理易求出其余两角.
70°、40°或55°、55°
;
引申:
已知等腰三角形的一个角是110°,求其余两角.
答案:其余两角为35°、35°.
归纳:等腰三角形的顶角可以是锐角、直角和钝角;
底角只能是锐角.所以,看到等腰三角形中的一个角的度数时,要注意判断这个角可能是顶角还是底角,是否需要分类讨论.
例2.如图:△ABC中,AB=AC,BD平分∠ABC交AC于D,若∠BDC=120°,求∠DBC的度数.
思路分析:由BD平分∠ABC,易知∠1=∠2,
则设∠1=∠2
=x,由AB=AC可得∠C=∠1+∠2=2x,在△DBC中由三角形内角和定理可列出x的方程,求出x.
例3.
在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.求∠A的度数.
思路分析:
由题设中的等边关系(AB=AC,BD=BC=AD),可以推出角的等量或倍数关系,在利用方程思想,可求出图中各角的度数.
1
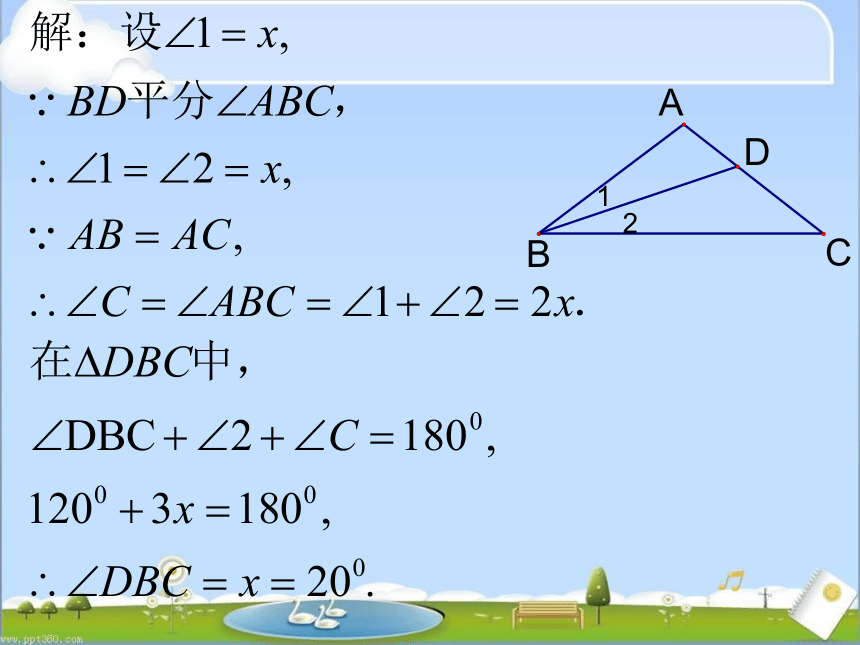
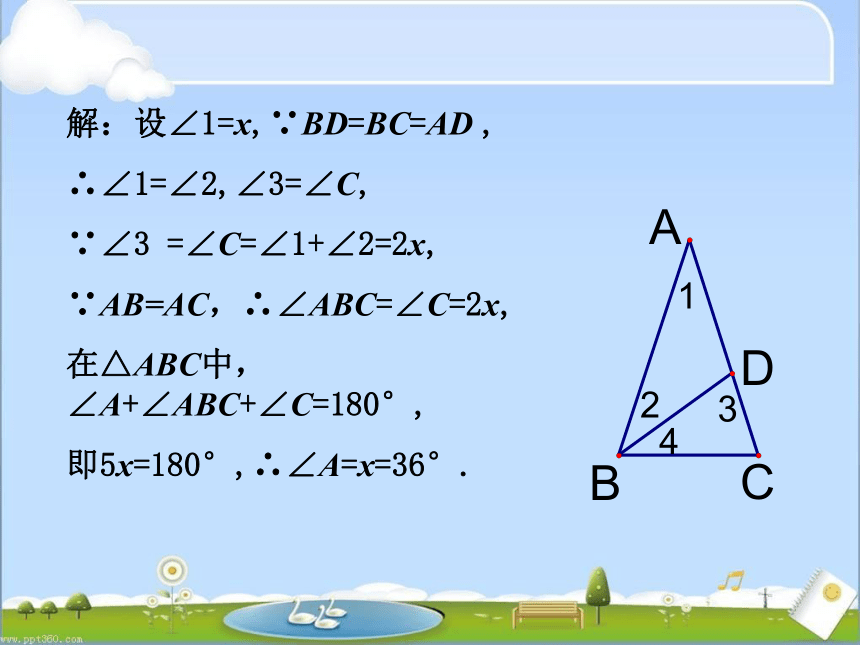
解:设∠1=x,∵BD=BC=AD
,
∴∠1=∠2,∠3=∠C,
∵∠3
=∠C=∠1+∠2=2x,
∵AB=AC,∴∠ABC=∠C=2x,
在△ABC中,∠A+∠ABC+∠C=180°,
即5x=180°,∴∠A=x=36°.
例4.
证明:等腰三角形底边中点到两腰的距离相等.
提示:
本题为文字命题,解题时应分为以下
三个步骤:
(1)根据题意作图;
(2)写出已知,
(3)进行求证.
例5.如图:在三角形ABC中,AB=AC,
BD⊥AC于D,求证:∠DBC=
∠A.
思路分析:由等腰三角形“三线合一”可联想到作底边的高,可推出1/2∠BAC=∠EAC,
由BD⊥AC,AE为高可知∠EAC和∠DBC都与∠C互余,推出∠DBC=∠EAC=1/2∠BAC.
E
E
证明:过点A作AE⊥BC于点E,
又∵AB=AC,
∴∠EAC
=1/2∠BAC,
∵BD⊥AC,AE为高可知,
∴∠EAC和∠DBC都与∠C互余,
∴∠DBC=∠EAC=1/2∠A
课间休息十分钟……
例6.在△ABC中,AB=AC,D是
CA延长线上一点,DF⊥BC于F,
交AB于E,求证:AE=AD.
思路分析:由等腰三角形“三线合一”可联想到作底边的高AM,可推出∠1=∠2,由DF⊥AC,AM⊥BC可知DF∥AM,从而∠3=∠4,证出结论.
M
1
3
4
2
3
4
1
2
证明:过点A作AM⊥BC于M,
∵AB=AC,
∴∠1=∠2,
∵DF⊥AC,AM⊥BC,
∴DF∥AM,
∴∠3=∠1,
∠2=∠4
∴∠3=∠4
,
∴AD=AE.
例7.如图,△ABC是正三角形,D、E、F分别是AB、BC、CA上的点,且AD=BE=CF,试说明△DEF是等边三角形.
思路分析:利用等边三角形的性质可推出,边、角的等量关系,从而易证三角形全等。进而说明△DEF是等边三角形.
证明:∵△ABC是正三角形,∴AB=BC=CA,∠A=∠B=∠C=60°,
又∵AD=BE=CF,
∴BD=EC=AF,
∴△ADF≌△BED≌△CFE,
∴DE=EF=DF
∴△DEF是等边三角形.
例8.如图,△ABD、
△AEC都是等边三角形,求证:
△AFG是等边三角形.
思路分析:利用等边三角形的性质可推出,边、角的等量关系,从而易证三角形全等,进而说明△AFG是等边三角形.
证明:∵△ABD
和△AED是正三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=60°,
∴
∠CAD=∠BAD+∠CAB=60°+∠CAB,
∠BAE=∠CAE+∠CAB=60°+∠CAB,
∴
∠CAD=∠BAE,
△ADC≌△BAE,
∴
∠ADF=∠GBA.
又∵AD=AB,
∠FAG=180°-∠BAD-∠CAE=60°,
∠FAG=∠DAF=60°,
∴△ADF≌△BAG,
∴AF=AG,
又∵∠FAG=60°,
∴△DEF是等边三角形.
例9.
求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
提示:本题为文字命题,首先应根据题意作图;写出已知,求证.
已知:∠CAE为△ABC的外角,∠1=∠2,
AD∥BC.求证:AB=AC
A
B
C
D
E
1
2
思路分析:欲证AB=AC
可
先证∠B=∠C,又∠1=∠2,所以应设法寻求∠B、∠C
与∠1、∠2的关系,又由
AD∥BC易得结论.
证明:
∵AD∥BC,
∴∠1=∠B(两直线平行,
同位角相等),
∠2=∠C(两直线平行,
内错角相等).
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等边对等角).
A
B
C
D
E
1
2
例10.已知:△ABC中,∠ABC=3∠C,
∠1=∠2,BE⊥AE.
求证:AC-AB=2BE.
思路分析:延长BE与AC交于点F,构造全等三角形∴△ABE≌△AFE,则2BE=BF,AC-AB=CF,我们只要判定△FBC为等腰三角形即可.
F
证明:延长BE与AC交于点F,
∵BE⊥AE.
∴∠AEB=∠AEF=90°
,
∵∠1=∠2,AE=AE,
∴△ABE≌△AFE,
∴2BE=BF,AB=AF,
∴AC-AB=AC-AF=FC,
∴∠ABF=∠AFB=∠FBC+∠C.
∵∠ABC=3∠C,
∴∠ABF+∠FBC=3∠C,
∴∠FBC+∠C+∠FBC=3∠C,
∴∠FBC=∠C,
∴BF=FC,
∴AC-AB=2BE.
