4.5 相似三角形判定定理的证明 同步练习(含解析)
文档属性
| 名称 | 4.5 相似三角形判定定理的证明 同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 15:21:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学北师大版九年级上学期 第四章 4.5 相似三角形判定定理的证明
单选题
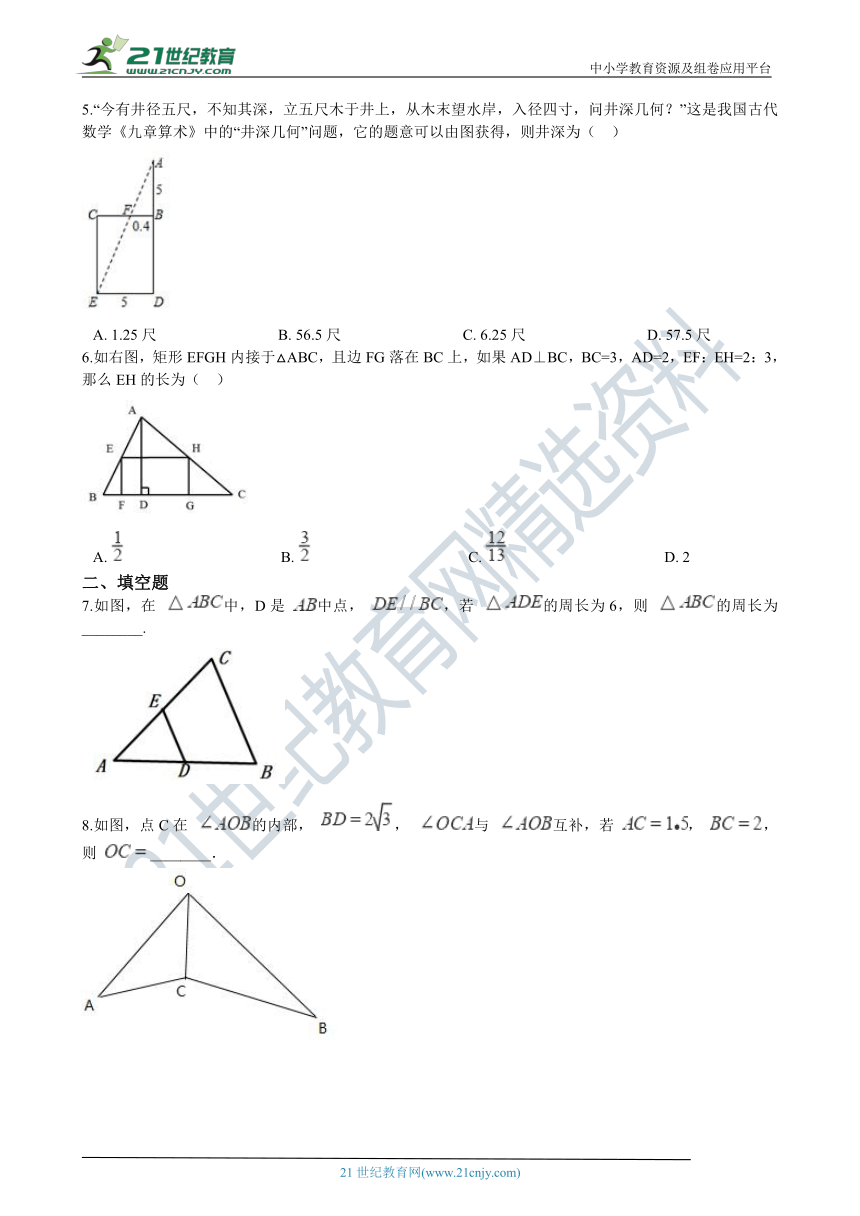
1.如图,在 中, ,四边形 的面积为21,则 的面积是(??? )
A.?????????????????????????????????????????B.?25????????????????????????????????????????C.?35????????????????????????????????????????D.?63
2.如图,正方形ABCD中,点E为BC右侧一点,∠AEC=90°,作DF⊥AE于点F,若CE=AF=2则正方形的面积为(??? ) 【来源:21·世纪·教育·网】
A.?16?????????????????????????????????????????B.?18?????????????????????????????????????????C.?20?????????????????????????????????????????D.?25
3.如图,点D,E分别_??????ABCè??_AB,AC上的一点,且DE∥BC,S△ADE=4,S四边形DBCE=5,则△ADE与△ABC相似比为(? ) 21·世纪*教育网
A.?5:9???????????????????????????????????B.?4:9???????????????????????????????????C.?16:81???????????????????????????????????D.?2:3
4.如图,在三角形ABC中,M,N分别是边AB,AC上的点,AM= AB,AN= AC,则三角形AMN的面积与四边形MBCN的面积比(??? ) 21*cnjy*com
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
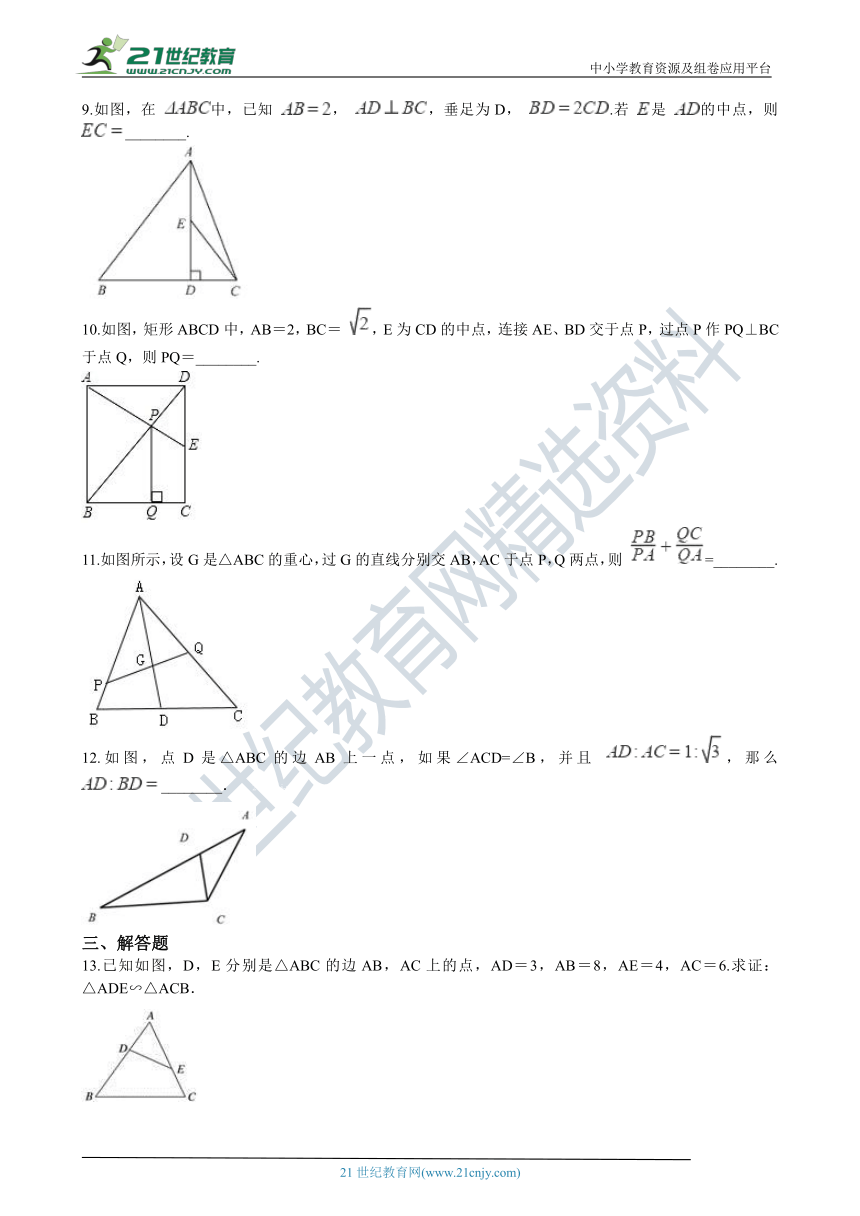
5.“今有井径五尺,不_???????·±?????????_尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为(?? )
A.?1.25尺????????????????????????????????B.?56.5尺????????????????????????????????C.?6.25尺????????????????????????????????D.?57.5尺
6.如右图,矩形EFGH内_?????????ABC_,且边FG落在BC上,如果AD⊥BC,BC=3,AD=2,EF:EH=2:3,那么EH的长为(?? ) 【版权所有:21教育】
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?2
二、填空题
7.如图,在 中,D是 中点, ,若 的周长为6,则 的周长为________.
?
8.如图,点C在 的内部, , 与 互补,若 , ,则 ________.
9.如图,在 中,已知 , ,垂足为D, .若 是 的中点,则 ________. 21*cnjy*com
10.如图,矩形ABCD中,AB=2,BC= ,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=________.
11.如图所示,设G是△ABC的重心,过G的直线分别交AB,AC于点P,Q两点,则 =________.
12.如图,点D是△ABC的边AB上一点,如果∠ACD=∠B,并且 ,那么 ________. 2-1-c-n-j-y
三、解答题
13.已知如图,D,E分别是△ABC的边AB,AC上的点,AD=3,AB=8,AE=4,AC=6.求证:△ADE∽△ACB.
四、综合题
14.已知,如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.
(1)求证:△ABD∽△CBA;
(2)在原图上作DE∥AB交AC与点E,请直接写出另一个与△ABD相似的三角形,并求出DE的长.
15.如图,在△AB_C??????AB???_AC , AD是边BC上的中线,BE⊥AC于点E , 交AD于点H过点C作CF∥AB交BE的延长线于点F . 21·cn·jy·com
(1)求证:△ABH∽△BFC;
(2)求证:BH2=HE?HF;
(3)若AB=2,∠BAC=45°,求BH的长.
答案解析部分
一、单选题
1.答案: B
解析:∵
∴
∴
∵
∴
∴
∴
∵
∴
∴
故答案为:B .
【分析】在 中, ,即可判断 ,然后由相似三角形的面积比等于相似比的平方,即可得出结果.
2.答案: C
解析:设AE和BC交于点M,
∵正方形ABCD,
∴设AD=AB=BC=x,∠DAF+∠MAB=90°,∠B=90°???
∵DF⊥AE
∴∠MAB+∠AMB=90°,∠B=∠DFA=90°
∴∠AMB=∠DAF
∴△DFA∽△ABM
∴即
解之:
同理可证△DFA∽△CEM
∴即
解之:
∵CM+BM=BC
∴
解之:x2=20
经检验x2=20是原方程的根.
∴正方形的面积为20.
故答案为:C. 2·1·c·n·j·y
【分析】设A_E???BC??¤???_点M,利用正方形的性质可知设AD=AB=BC=x,∠DAF+∠MAB=90°,∠B=90° ;再证明∠AMB=∠DAF,∠B=∠DFA,由此可证得△DFA∽△ABM,利用相似三角形的对应边成比例可表示出BM的长,同理可证△DFA∽△CEM,利用相似三角形的性质可表示出CM的长;然后根据CM+BM=BC,建立关于x的方程,解方程求出x2即可。【出处:21教育名师】
3.答案: D
解析:∵DE∥BC,
∴△ADE∽△ABC,
∴
∴ ,
即△ADE与△ABC相似比为2:3.
故答案为:D.
【分析】先说明△ADE∽△ABC,然后利用相似三角形的性质求解即可.
4.答案: B
解析:∵AM= AB,AN= AC,∠MAN=∠BAC,
∴ = , = ,
∴△MAN∽△BAC,
∴ =( )2= ,
∴三角形AMN的面积与四边形MBCN的面积比为1:15,
故答案为:B.
【分析】根据AM= AB,AN= AC,∠MAN=∠BAC,可以得到△MAN∽△BAC,然后相似三角形的面积之比等于相似比的平方,从而可以得到△AMN和△ABC的面积之比,然后即可得到三角形AMN的面积与四边形MBCN的面积比,本题得以解决.21教育名师原创作品
5.答案: D
解析:依题意有△ABF∽△ADE,
∴AB:AD=BF:DE,
即5:AD=0.4:5,
解得AD=62.5,
BD=AD?AB=62.5?5=57.5尺.
故答案为:D.
【分析】根据平行与三角形一边_?????????(?????¤_边的延长线)和其他两边相交,所构成的三角形与原三角形相似可得△ABF∽△ADE,于是可得比例式AB:AD=BF:DE求得AD的值,再根据BD=AD?AB可求解.
6.答案: B
解析:∵四边形EFGH是矩形,
∴EH//BC,
∴△AEH∽△ABC,
∵AM⊥EH,AD⊥BC,
∴
设EH=3x,则有EF=2x,AM=AD-EF=2-2x,
∴
解得:x= ,
则EH=3x= .
故答案为B.
【分析】设EH=3x_??????EF=2_x,△AEH的边EH上的高为AM=AD-EF,再由三角形AEH与三角形ABC相似,利用相似三角形对应边上的高之比等于相似比求出x的值,进而求得EH的长.
二、填空题
7.答案: 12
解析:∵ ,
∴ ,
又∵D是 中点,
∴ ,即 与 的相似比为1:2,
∴ 与 的周长比为1:2,
∵ 的周长为6,
∴ 的周长为12,
故答案为:12.
【分析】由 ,可知 ,再由D是 中点,可得到相似比,即可求出 的周长.
8.答案:
解析:∵∠OCA=∠OCB,∠OCA与∠AOB互补,
∴∠OCA+∠AOB=180°,∠OCB+∠AOB=180°,
∵∠OCA+∠COA+∠OAC=180°,∠OCB+∠OBC+∠COB=180°,
∴∠AOB=∠COA+∠OAC,∠AOB=∠OBC+∠COB,
∴∠AOC=∠OBC,∠COB=∠OAC,
∴△ACO∽△OCB,
∴ ,
∴OC2=2× =3,
∴OC= ,
故答案为: .
【分析】通过证明△ACO∽△OCB,可得 ,可求出OC.
9.答案: 1
解析:
为 的中点,
,
∴ ,
,
故答案为:1.
【分析】根据“两边对应成比例,夹角相等的两个三角形相似”证明△ADB∽△EDC,得 ,由AB=2则可求出结论.21cnjy.com
10.答案:
解析:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,AD=BC,∠BAD=90°,
∵E为CD的中点,
∴DE= CD= AB,
∴△ABP∽△EDP,
∴ = ,
∴ = ,
∴ = ,
∵PQ⊥BC,
∴PQ∥CD,
∴△BPQ∽△DBC,
∴ = = ,
∵CD=2,
∴PQ= ,
故答案为: .
【分析】根据矩形的性质得到AB∥CD,AB=CD,AD=BC,∠BAD=90°,根据线段中点的定义得到DE= CD= AB,易得△BPQ∽△DBC,根据相似三角形的性质可得比例式求解.21教育网
11.答案: 1
解析:过点B,C作BE∥AD,CF∥AD,交直线PQ于点E,F
∴四边形BEFC是梯形
∵G是重心,
∴点D是BC的中点,点G是EF的中点,AG=2DG,???
∴DG是梯形BEFC的中位线
∴BE+CF=2DG
∵BE∥AD,CF∥AD
∴
故答案为:1.
【分析】 过点B,C作BE∥AD,CF∥AD,交直线PQ于点E,F,易证四边形BEFC是梯形,再利用重心的定义及性质,可得点D是BC的中点,点G是EF的中点,AG=2DG,利用梯形的中位线定理可得到BE+CF=2DG,利用平行线分线段成比例定理可求出的值。www.21-cn-jy.com
12.答案:
解析:在△ACD与△ABC中,
∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴
∴AD= ,AB= AC
∴BD=AB-AD=
∴ ∶ =1∶2
故答案为1∶2.
【分析】根据两角分别相等的两个三角形相似,可得△ACD∽△ABC的关系,最后根据相似三角形的性质和线段的和差即可解答.21世纪教育网版权所有
三、解答题
13.答案: 证明:∵AD=3,AB=8,AE=4,AC=6,
∴ = = ,
又∵∠DAE=∠CAB,
∴△ADE∽△ACB.
解析:根据已知的线段长度知 = ,又∠DAE=∠CAB可得△ADE∽△ACB.
四、综合题
14.答案: (1)证明:∵AB=2,BC=4,BD=1
∴AB:CB=BD:BA
∵∠ABD=∠CBA
∴△ABD∽△CBA;
(2)解:∵DE∥AB
∴△CDE∽△CBA
∴△ABD∽△CDE
∴AB:BD=CD:D
∴2:1=3:DE
∴DE=1.5.
解析:(1_?????¨???ABD_与△CBA中,有∠B=∠B , 根据已知边的条件,只需证明夹此角的两边对应成比例即可;(2)由(1)知△ABD∽△CBA , 又DE∥AB , 易证△CDE∽△CBA , 则:△ABD∽△CDE , 然后根据相似三角形的对应边成比例得出DE的长.www-2-1-cnjy-com
15.答案: (1)证明:∵AB=AC,AD是边BC上的中线,
∴∠BAD=∠CAD,AD⊥BC,
∵BE⊥AC,
∴∠BDH=∠AEH=90°,
∵∠AHE=∠BHD,
∴∠DBH=∠DAC=∠BAD,
∵CF∥AB,
∴∠ABH=∠F,
∴△ABH∽△BFC;
(2)证明:连接CH.∵AD⊥BC,BD=DC,
∴BH=HC,
∴∠HBC=∠HCB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABH=∠ACH,
∵CF∥AB,
∴∠ABH=∠F,
∴∠HCE=∠F,
∵∠CHE=∠CHF,
∴△CHE∽△FHC,
∴ ,
∴HC2=HE?HF,
∵BH=HC,
∴BH2=HE?HF;
(3)解:延长CH交AB于M,由题意CM⊥AB,
∵BE⊥AC,∠BAC=45°,
∴∠ABE=45°,
∴AE=AB?cos45°=2× = ,
∵∠HAM=∠HAE,∠HMA=∠HEA,∠AMH=∠AEH=90°,
∴△AHM≌△AHE(AAS),
∴AM=AE= ,
∴BM=AB﹣AM=2﹣ ,
在Rt△BHM中,BH= =2 ﹣2.
解析:_???1??????_据两角对应相等两三角形相似证明即可;(2)连接CH , 首先证明BH=HC , 再证明△CHE∽△FHC可得结论;(3)延长CH交AB于M , 由题意CM⊥AB . 利用全等三角形的性质证明AM=AE=2,求出BM即可解决问题.【来源:21cnj*y.co*m】
_21?????????è?????(www.21cnjy.com)_
初中数学北师大版九年级上学期 第四章 4.5 相似三角形判定定理的证明
单选题
1.如图,在 中, ,四边形 的面积为21,则 的面积是(??? )
A.?????????????????????????????????????????B.?25????????????????????????????????????????C.?35????????????????????????????????????????D.?63
2.如图,正方形ABCD中,点E为BC右侧一点,∠AEC=90°,作DF⊥AE于点F,若CE=AF=2则正方形的面积为(??? ) 【来源:21·世纪·教育·网】
A.?16?????????????????????????????????????????B.?18?????????????????????????????????????????C.?20?????????????????????????????????????????D.?25
3.如图,点D,E分别_??????ABCè??_AB,AC上的一点,且DE∥BC,S△ADE=4,S四边形DBCE=5,则△ADE与△ABC相似比为(? ) 21·世纪*教育网
A.?5:9???????????????????????????????????B.?4:9???????????????????????????????????C.?16:81???????????????????????????????????D.?2:3
4.如图,在三角形ABC中,M,N分别是边AB,AC上的点,AM= AB,AN= AC,则三角形AMN的面积与四边形MBCN的面积比(??? ) 21*cnjy*com
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
5.“今有井径五尺,不_???????·±?????????_尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为(?? )
A.?1.25尺????????????????????????????????B.?56.5尺????????????????????????????????C.?6.25尺????????????????????????????????D.?57.5尺
6.如右图,矩形EFGH内_?????????ABC_,且边FG落在BC上,如果AD⊥BC,BC=3,AD=2,EF:EH=2:3,那么EH的长为(?? ) 【版权所有:21教育】
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?2
二、填空题
7.如图,在 中,D是 中点, ,若 的周长为6,则 的周长为________.
?
8.如图,点C在 的内部, , 与 互补,若 , ,则 ________.
9.如图,在 中,已知 , ,垂足为D, .若 是 的中点,则 ________. 21*cnjy*com
10.如图,矩形ABCD中,AB=2,BC= ,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=________.
11.如图所示,设G是△ABC的重心,过G的直线分别交AB,AC于点P,Q两点,则 =________.
12.如图,点D是△ABC的边AB上一点,如果∠ACD=∠B,并且 ,那么 ________. 2-1-c-n-j-y
三、解答题
13.已知如图,D,E分别是△ABC的边AB,AC上的点,AD=3,AB=8,AE=4,AC=6.求证:△ADE∽△ACB.
四、综合题
14.已知,如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.
(1)求证:△ABD∽△CBA;
(2)在原图上作DE∥AB交AC与点E,请直接写出另一个与△ABD相似的三角形,并求出DE的长.
15.如图,在△AB_C??????AB???_AC , AD是边BC上的中线,BE⊥AC于点E , 交AD于点H过点C作CF∥AB交BE的延长线于点F . 21·cn·jy·com
(1)求证:△ABH∽△BFC;
(2)求证:BH2=HE?HF;
(3)若AB=2,∠BAC=45°,求BH的长.
答案解析部分
一、单选题
1.答案: B
解析:∵
∴
∴
∵
∴
∴
∴
∵
∴
∴
故答案为:B .
【分析】在 中, ,即可判断 ,然后由相似三角形的面积比等于相似比的平方,即可得出结果.
2.答案: C
解析:设AE和BC交于点M,
∵正方形ABCD,
∴设AD=AB=BC=x,∠DAF+∠MAB=90°,∠B=90°???
∵DF⊥AE
∴∠MAB+∠AMB=90°,∠B=∠DFA=90°
∴∠AMB=∠DAF
∴△DFA∽△ABM
∴即
解之:
同理可证△DFA∽△CEM
∴即
解之:
∵CM+BM=BC
∴
解之:x2=20
经检验x2=20是原方程的根.
∴正方形的面积为20.
故答案为:C. 2·1·c·n·j·y
【分析】设A_E???BC??¤???_点M,利用正方形的性质可知设AD=AB=BC=x,∠DAF+∠MAB=90°,∠B=90° ;再证明∠AMB=∠DAF,∠B=∠DFA,由此可证得△DFA∽△ABM,利用相似三角形的对应边成比例可表示出BM的长,同理可证△DFA∽△CEM,利用相似三角形的性质可表示出CM的长;然后根据CM+BM=BC,建立关于x的方程,解方程求出x2即可。【出处:21教育名师】
3.答案: D
解析:∵DE∥BC,
∴△ADE∽△ABC,
∴
∴ ,
即△ADE与△ABC相似比为2:3.
故答案为:D.
【分析】先说明△ADE∽△ABC,然后利用相似三角形的性质求解即可.
4.答案: B
解析:∵AM= AB,AN= AC,∠MAN=∠BAC,
∴ = , = ,
∴△MAN∽△BAC,
∴ =( )2= ,
∴三角形AMN的面积与四边形MBCN的面积比为1:15,
故答案为:B.
【分析】根据AM= AB,AN= AC,∠MAN=∠BAC,可以得到△MAN∽△BAC,然后相似三角形的面积之比等于相似比的平方,从而可以得到△AMN和△ABC的面积之比,然后即可得到三角形AMN的面积与四边形MBCN的面积比,本题得以解决.21教育名师原创作品
5.答案: D
解析:依题意有△ABF∽△ADE,
∴AB:AD=BF:DE,
即5:AD=0.4:5,
解得AD=62.5,
BD=AD?AB=62.5?5=57.5尺.
故答案为:D.
【分析】根据平行与三角形一边_?????????(?????¤_边的延长线)和其他两边相交,所构成的三角形与原三角形相似可得△ABF∽△ADE,于是可得比例式AB:AD=BF:DE求得AD的值,再根据BD=AD?AB可求解.
6.答案: B
解析:∵四边形EFGH是矩形,
∴EH//BC,
∴△AEH∽△ABC,
∵AM⊥EH,AD⊥BC,
∴
设EH=3x,则有EF=2x,AM=AD-EF=2-2x,
∴
解得:x= ,
则EH=3x= .
故答案为B.
【分析】设EH=3x_??????EF=2_x,△AEH的边EH上的高为AM=AD-EF,再由三角形AEH与三角形ABC相似,利用相似三角形对应边上的高之比等于相似比求出x的值,进而求得EH的长.
二、填空题
7.答案: 12
解析:∵ ,
∴ ,
又∵D是 中点,
∴ ,即 与 的相似比为1:2,
∴ 与 的周长比为1:2,
∵ 的周长为6,
∴ 的周长为12,
故答案为:12.
【分析】由 ,可知 ,再由D是 中点,可得到相似比,即可求出 的周长.
8.答案:
解析:∵∠OCA=∠OCB,∠OCA与∠AOB互补,
∴∠OCA+∠AOB=180°,∠OCB+∠AOB=180°,
∵∠OCA+∠COA+∠OAC=180°,∠OCB+∠OBC+∠COB=180°,
∴∠AOB=∠COA+∠OAC,∠AOB=∠OBC+∠COB,
∴∠AOC=∠OBC,∠COB=∠OAC,
∴△ACO∽△OCB,
∴ ,
∴OC2=2× =3,
∴OC= ,
故答案为: .
【分析】通过证明△ACO∽△OCB,可得 ,可求出OC.
9.答案: 1
解析:
为 的中点,
,
∴ ,
,
故答案为:1.
【分析】根据“两边对应成比例,夹角相等的两个三角形相似”证明△ADB∽△EDC,得 ,由AB=2则可求出结论.21cnjy.com
10.答案:
解析:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,AD=BC,∠BAD=90°,
∵E为CD的中点,
∴DE= CD= AB,
∴△ABP∽△EDP,
∴ = ,
∴ = ,
∴ = ,
∵PQ⊥BC,
∴PQ∥CD,
∴△BPQ∽△DBC,
∴ = = ,
∵CD=2,
∴PQ= ,
故答案为: .
【分析】根据矩形的性质得到AB∥CD,AB=CD,AD=BC,∠BAD=90°,根据线段中点的定义得到DE= CD= AB,易得△BPQ∽△DBC,根据相似三角形的性质可得比例式求解.21教育网
11.答案: 1
解析:过点B,C作BE∥AD,CF∥AD,交直线PQ于点E,F
∴四边形BEFC是梯形
∵G是重心,
∴点D是BC的中点,点G是EF的中点,AG=2DG,???
∴DG是梯形BEFC的中位线
∴BE+CF=2DG
∵BE∥AD,CF∥AD
∴
故答案为:1.
【分析】 过点B,C作BE∥AD,CF∥AD,交直线PQ于点E,F,易证四边形BEFC是梯形,再利用重心的定义及性质,可得点D是BC的中点,点G是EF的中点,AG=2DG,利用梯形的中位线定理可得到BE+CF=2DG,利用平行线分线段成比例定理可求出的值。www.21-cn-jy.com
12.答案:
解析:在△ACD与△ABC中,
∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴
∴AD= ,AB= AC
∴BD=AB-AD=
∴ ∶ =1∶2
故答案为1∶2.
【分析】根据两角分别相等的两个三角形相似,可得△ACD∽△ABC的关系,最后根据相似三角形的性质和线段的和差即可解答.21世纪教育网版权所有
三、解答题
13.答案: 证明:∵AD=3,AB=8,AE=4,AC=6,
∴ = = ,
又∵∠DAE=∠CAB,
∴△ADE∽△ACB.
解析:根据已知的线段长度知 = ,又∠DAE=∠CAB可得△ADE∽△ACB.
四、综合题
14.答案: (1)证明:∵AB=2,BC=4,BD=1
∴AB:CB=BD:BA
∵∠ABD=∠CBA
∴△ABD∽△CBA;
(2)解:∵DE∥AB
∴△CDE∽△CBA
∴△ABD∽△CDE
∴AB:BD=CD:D
∴2:1=3:DE
∴DE=1.5.
解析:(1_?????¨???ABD_与△CBA中,有∠B=∠B , 根据已知边的条件,只需证明夹此角的两边对应成比例即可;(2)由(1)知△ABD∽△CBA , 又DE∥AB , 易证△CDE∽△CBA , 则:△ABD∽△CDE , 然后根据相似三角形的对应边成比例得出DE的长.www-2-1-cnjy-com
15.答案: (1)证明:∵AB=AC,AD是边BC上的中线,
∴∠BAD=∠CAD,AD⊥BC,
∵BE⊥AC,
∴∠BDH=∠AEH=90°,
∵∠AHE=∠BHD,
∴∠DBH=∠DAC=∠BAD,
∵CF∥AB,
∴∠ABH=∠F,
∴△ABH∽△BFC;
(2)证明:连接CH.∵AD⊥BC,BD=DC,
∴BH=HC,
∴∠HBC=∠HCB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABH=∠ACH,
∵CF∥AB,
∴∠ABH=∠F,
∴∠HCE=∠F,
∵∠CHE=∠CHF,
∴△CHE∽△FHC,
∴ ,
∴HC2=HE?HF,
∵BH=HC,
∴BH2=HE?HF;
(3)解:延长CH交AB于M,由题意CM⊥AB,
∵BE⊥AC,∠BAC=45°,
∴∠ABE=45°,
∴AE=AB?cos45°=2× = ,
∵∠HAM=∠HAE,∠HMA=∠HEA,∠AMH=∠AEH=90°,
∴△AHM≌△AHE(AAS),
∴AM=AE= ,
∴BM=AB﹣AM=2﹣ ,
在Rt△BHM中,BH= =2 ﹣2.
解析:_???1??????_据两角对应相等两三角形相似证明即可;(2)连接CH , 首先证明BH=HC , 再证明△CHE∽△FHC可得结论;(3)延长CH交AB于M , 由题意CM⊥AB . 利用全等三角形的性质证明AM=AE=2,求出BM即可解决问题.【来源:21cnj*y.co*m】
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
