4.8 图形的位似 同步练习（含解析）

中小学教育资源及组卷应用平台
初中数学北师大版九年级上学期 第四章 4.8 图形的位似
一、单选题
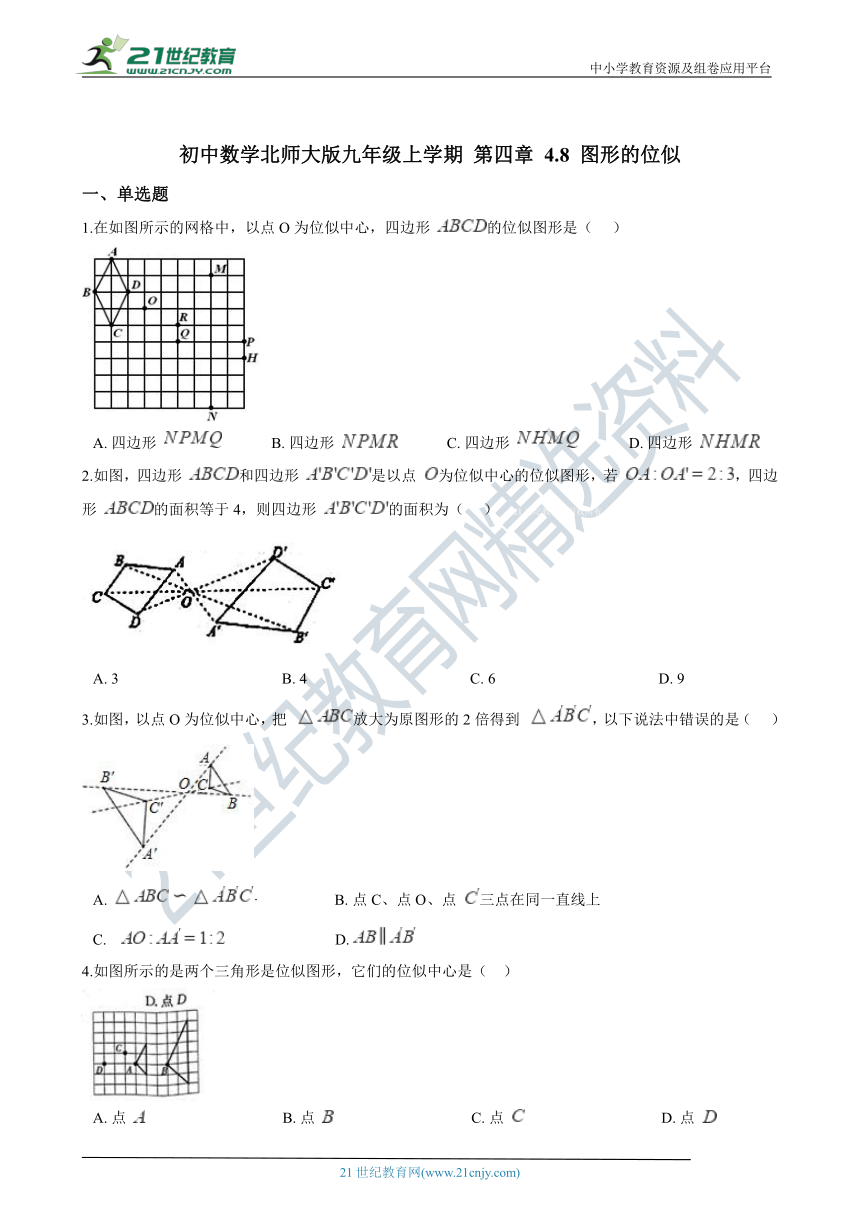
1.在如图所示的网格中，以点O为位似中心，四边形 的位似图形是（??? ）
A.?四边形 ?????????????B.?四边形 ?????????????C.?四边形 ?????????????D.?四边形
2.如图，四边形 和四边形 是以点 为位似中心的位似图形，若 ，四边形 的面积等于4，则四边形 的面积为（??? ） 21世纪教育网版权所有
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?6???????????????????????????????????????????D.?9
3.如图，以点O为位似中心，把 放大为原图形的2倍得到 ，以下说法中错误的是（??? ）
A.?·????????????????????B.?点C、点O、点 三点在同一直线上
C.?? ??? ??D.?21教育网
4.如图所示的是两个三角形是位似图形，它们的位似中心是（ ??）
A.?点 ????????????????????????????????????B.?点 ????????????????????????????????????C.?点 ????????????????????????????????????D.?点
二、填空题
5.在平面直角坐标系中， 和 的相似比等于 ，并且是关于原点O的位似图形，若点A的坐标为 ，则其对应点 的坐标是________． www.21-cn-jy.com
6.如图，以点O为位似中心，将 放大后得到 ， ，则 ________．
7.如图，△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形，且 = ，已知点A（﹣1，0），点C（ ，1），则A'C'=________. 21·世纪*教育网
8.如图，在平面直角坐标系中，_??????AB??¤???_端点的坐标分别为A（2.5，5），B（5，0），以坐标原点为位似中心，将线段AB在第一象限内缩小得到线段CD，其中点A对应点C，点B对应点D，若点C的坐标为（1.25，2.5），则点D的坐标为________． www-2-1-cnjy-com
9.如图，在平面直角坐标系中，_???ABC??????_A′B′C′是以坐标原点O为位似中心的位似图形，且点B(3，1)，B′(6，2)，若点A′(5，6)，则A的坐标为________. 2-1-c-n-j-y
三、作图题
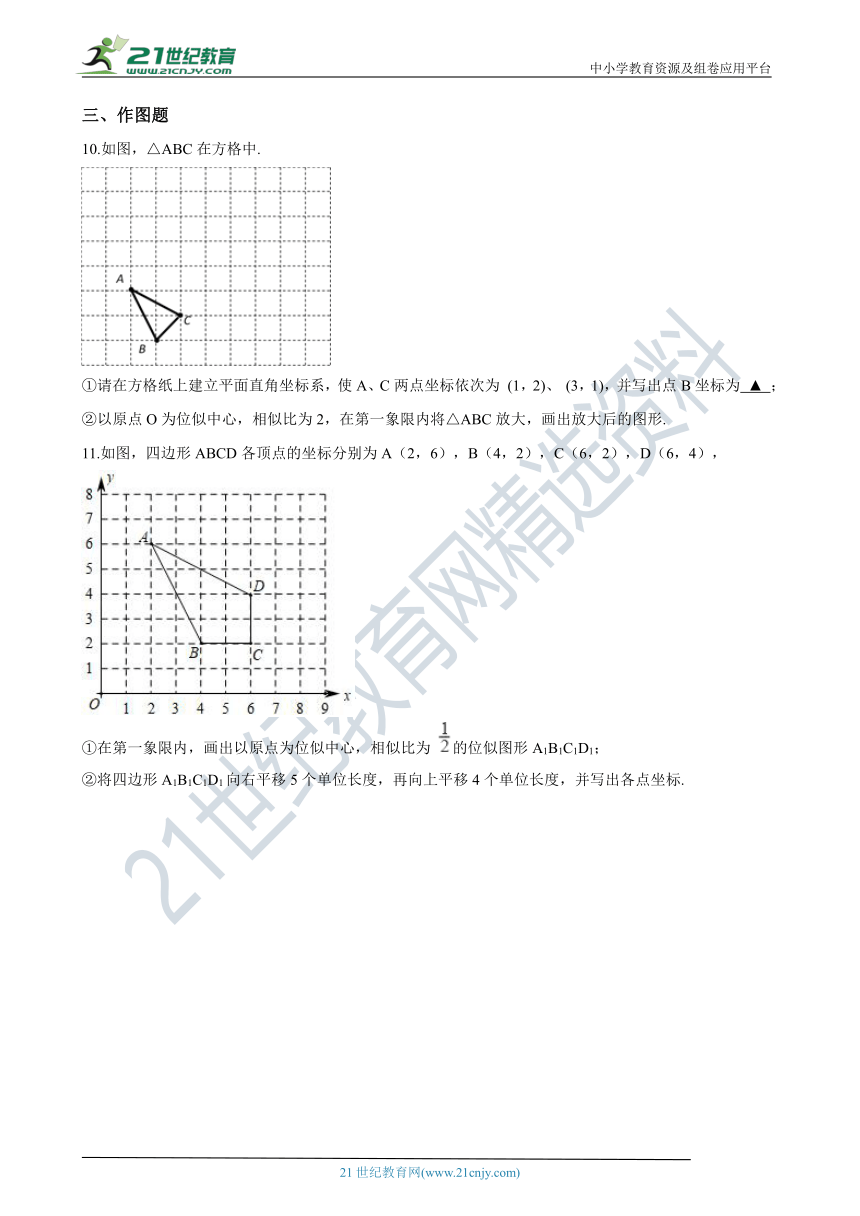
10.如图，△ABC在方格中.
①请在方格纸上建立平面直角坐标系，使A、C两点坐标依次为 (1，2)、 (3，1)，并写出点B坐标为 ▲ ；
②以原点O为位似中心，相似比为2，在第一象限内将△ABC放大，画出放大后的图形.
11.如图，四边形ABCD各顶点的坐标分别为A（2，6），B（4，2），C（6，2），D（6，4），
①在第一象限内，画出以原点为位似中心，相似比为 的位似图形A1B1C1D1；
②将四边形A1B1C1D1向右平移5个单位长度，再向上平移4个单位长度，并写出各点坐标.
答案解析部分
一、单选题
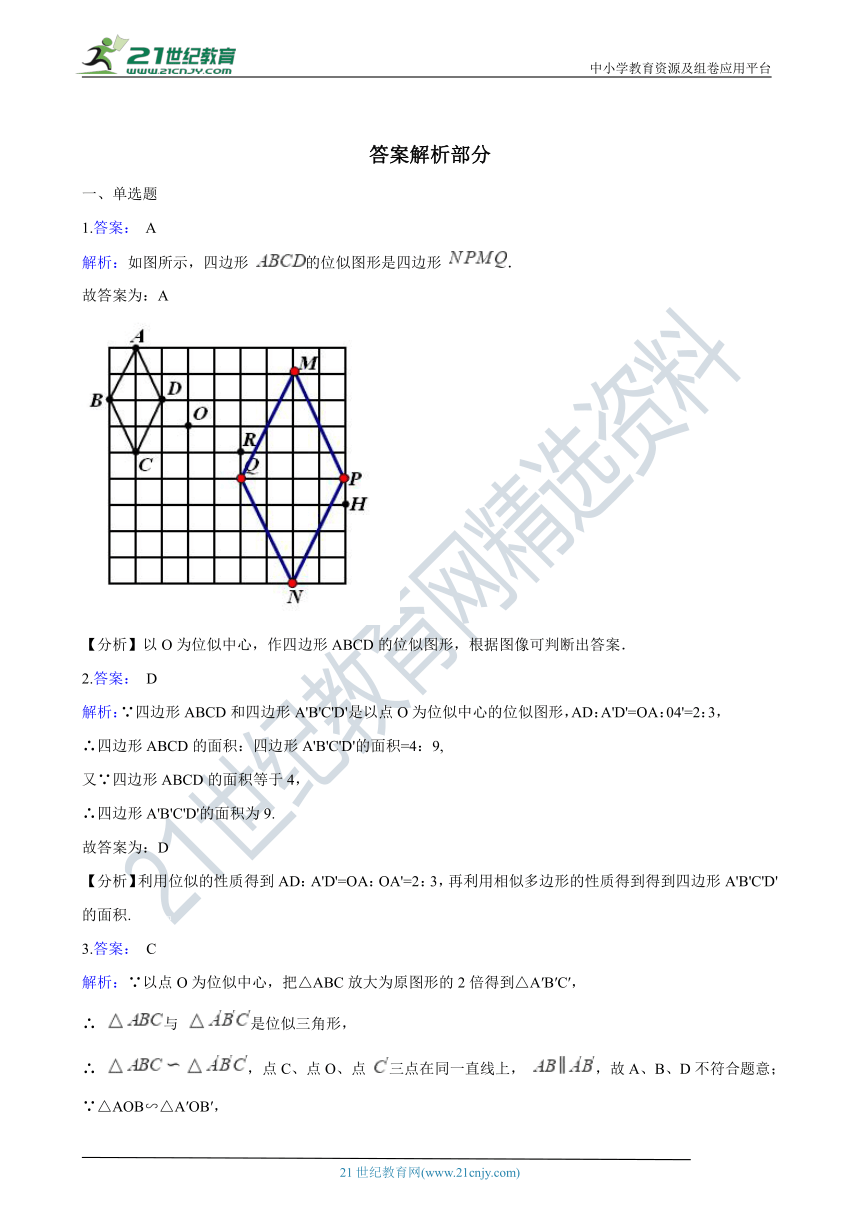
1.答案： A
解析：如图所示，四边形 的位似图形是四边形 ．
故答案为：A
【分析】以O为位似中心，作四边形ABCD的位似图形，根据图像可判断出答案．
2.答案： D
解析：∵四边形ABCD和四边形A'B'C'D'是以点O为位似中心的位似图形，AD：A'D'=OA：04'=2：3， 21*cnjy*com
∴四边形ABCD的面积：四边形A'B'C'D'的面积=4：9,
又∵四边形ABCD的面积等于4，
∴四边形A'B'C'D'的面积为9.
故答案为：D
【分析】利用位似的性质得到AD：A'D'=OA：OA'=2：3，再利用相似多边形的性质得到得到四边形A'B'C'D'的面积.21cnjy.com
3.答案： C
解析：∵以点O为位似中心，把△ABC放大为原图形的2倍得到△A′B′C′，
∴ 与 是位似三角形，
∴ ，点C、点O、点 三点在同一直线上， ，故A、B、D不符合题意；
∵△AOB∽△A′OB′，
∴OA：OA′=AB：A′B′=1：2，
∴OA：AA′=1：3，故C符合题意；
故答案为：C．
【分析】根据位似的性质解答即可．
4.答案： D
解析：如图所示，它们的位似中心是点D
故答案为：D.
【分析】根据位似中心的定义“对应顶点的连线相交于一点，这一点即为位似中心”可求解.
二、填空题
5.答案： （4，8）或（﹣4，﹣8）
解析：在同一象限内，
∵ ABC与 是以原点O为位似中心的位似图形，其中相似比等于 ，A坐标为（2，4），
∴则点 的坐标为：（4，8），
不在同一象限内，
∵ ABC与 是以原点O为位似中心的位似图形，其中相似比等于 ，A坐标为（2，4），
∴则点A′的坐标为：（﹣4，﹣8），
故答案为：（4，8）或（﹣4，﹣8）．
【分析】根据在平面直角坐标系_??????????????????_变换是以原点为位似中心，相似比为k ， 那么位似图形对应点的坐标的比等于k或﹣k ， 即可求得答案．2·1·c·n·j·y
6.答案：
解析：∵以点O为位似中心，将 放大后得到 ， ，
∴ ．
故答案为： ．
【分析】直接利用位似图形的性质进而分析得出答案．
7.答案：
解析：过点C'作C'D⊥x轴于点D,

∵△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形， =
∴点C是OC'的中点，点A是OA'的中点
∵点A（﹣1，0），点C（ ，1）
∴点A'（-2，0），点C'（1，2）
∴OA'=2，DC'=2，OD=1,
∴A'D=OA'+OD=2+1=3,
∴A'C'=.
故答案为：.
【分析】过点C'作C'D⊥x轴于点D，根据已知△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形，由OA于OA'的比值可知点C是OC'的中点，点A是OA'的中点，由点A，C的坐标，就可求出点A'，C'的坐标，由此可求出OA'，DC'，OD，A'D的长，然后利用勾股定理求出A'C'的长。
8.答案： （2.5，0）
解析：∵将线段AB缩小得到线段CD，点A（2.5，5）的对应点C的坐标为（1.25，2.5），
∴线段AB缩小 得到线段CD，
∴点D的坐标为（2.5，0）．
故答案为：（2.5，0）．
【分析】利用点A和点C的坐标之间的关系得到线段AB缩小 得到线段CD，然后确定D点坐标．
9.答案： (2.5，3)
解析：∵点B(3，1)，B′(6，2)，点A′(5，6)，
∴A的坐标为：(2.5，3).
故答案为：(2.5，3).
【分析】利用点B(3，1)，B′(6，2)即可得出位似比进而得出A的坐标.
三、作图题
10.答案： 解：如图所示，△A′B′C′即为所求.
则B的坐标为：（2，0）；
解析：（1）直接利用A、C两点坐标得出原点位置进而得出答案；
（2）利用位似图形的性质得出对应点位置进而得出答案.21·cn·jy·com
11.答案： 解：如图所示，四边形A1B1C1D1、四边形A2B2C2D2即为所求.
其中A2（6，7）、B2（7，5）、C2（8，5）、D2（8，6）.
解析：_??????????????????_换的概念分别作出四个顶点的对应点，再首尾顺次连接即可得；②根据平移变换的概念作出变换后的对应点，再首尾顺次连接即可得.【来源：21·世纪·教育·网】
_21?????????è?????(www.21cnjy.com)_