湘教版八年级数学上册第2章三角形单元测试卷(word版含答案)
文档属性
| 名称 | 湘教版八年级数学上册第2章三角形单元测试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 547.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 16:44:25 | ||
图片预览




文档简介
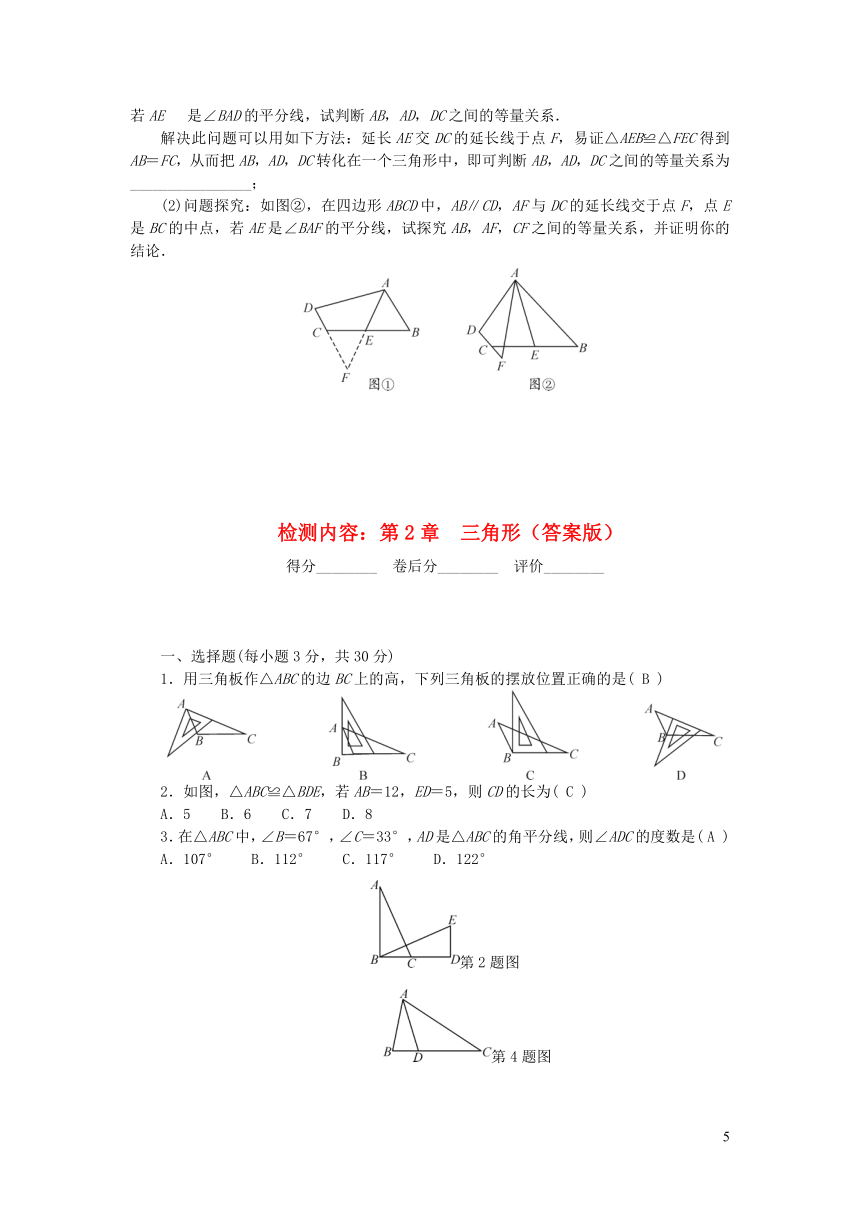
检测内容:第2章 三角形
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是(
)
2.如图,△ABC≌△BDE,若AB=12,ED=5,则CD的长为(
)
A.5
B.6
C.7
D.8
3.在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠ADC的度数是(
)
A.107°
B.112°
C.117°
D.122°
第2题图
第4题图
第8题图
第9题图
4.(苏州中考)如图,在△ABC中,点D在边BC上,AB=AD=DC,∠B=80°,则∠C的度数为(
)
A.30°
B.40°
C.45°
D.60°
5.在△ABC中,∠A=∠B=∠C,则此三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
6.已知不等边三角形的两边长分别是2
cm和9
cm,如果第三边的长为整数,那么第三边的长为(
)
A.8
cm
B.10
cm
C.8
cm或10
cm
D.8
cm或9
cm
7.下列条件中,能作出唯一三角形的是(
)
A.已知三边作三角形
B.已知两边及一角作三角形
C.已知两角及一边作三角形
D.已知一锐角和一直角边作直角三角形
8.如图,在△ABC中,∠A=30°,∠C=90°,AB的垂直平分线交AC于点D,交AB于点E,则下列结论错误的是(
)
A.AD=DB
B.∠BDE=60°
C.BC=AD
D.△ADE≌△BDC
9.如图,∠ADB=∠ACB=90°,OA=OB,且AC,BD交于点O.有下列说法:①AD=BC;②AC=BD;③∠DCA=∠CDB;④AB∥CD.其中正确的说法有(
)
A.1个
B.2个
C.3个
D.4个
10.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③EF=AP;④S四边形AEPF=S△ABC.当∠EPF在△ABC内绕P旋转时(点E不与A,B重合),上述结论始终正确的有(
)
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共24分)
11.如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.你添加的条件是________________
(不再添加辅助线和字母).
12.命题“互为相反数的两个数之和等于0”的逆命题是:___________________________________________________,它是________________命题(填“真”或“假”).
13.在△ABC中,三边的长分别为a,b,c,且满足(a-b)2+(b-c)2=0,则这个三角形一定是________________.
14.如图,△AOB≌△DOC,△AOB的周长为10,且BC=4,则△DBC的周长为________________.
15.(2019·江西)如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE=________________.
16.如图,在长方形ABCD中,把△DBC沿BD折叠得△BDC′,则图中共有________________对全等三角形.
17.如图,AB∥CD,∠BAC与∠ACD的平分线相交于点O,OE⊥AC于点E,且OE=5
cm,则直线AB与CD之间的距离为________________
cm.
18.如图,△ABC的面积为4
cm2,BP平分∠ABC,且AP⊥BP于点P,则△PBC的面积为________________cm2.
三、解答题(共66分)
19.(6分)如图,已知∠MON,点A,B在OM上,点C在∠MON的平分线上,且点C到A,B两点的距离相等,用尺规作图画出点C.(不写作法,但要保留作图痕迹)
20.(6分)如图,AD是△ABC的角平分线,∠B=45°,点E在BC的延长线上且EH⊥AD于点H.若∠ACB=85°,求∠E的度数.
21.(6分)如图,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,请你找出图中的全等的三角形,并证明你的结论.
22.(8分)如图所示,点D为码头,A,B为灯塔,A,B两个灯塔到码头D的距离相等,DA,DB为海岸线.一轮船离开码头,计划沿∠ADB的平分线航行.在航行途中C点处,测得轮船到灯塔A和灯塔B的距离相等.试问:轮船航行时,是否偏离了预定的航线,请说明理由.
23.(8分)王强同学用10块高度都是2
cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.
24.(10分)(2019·杭州)如图,在△ABC中,AC<AB<BC.
(1)已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B;
(2)以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连接AQ.若∠AQC=3∠B,求∠B的度数.
25.(10分)如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点E在线段CA上由C点向A点运动.当点E的运动速度为多少厘米/秒时,能够在某一时刻使△BPD与△CEP全等.
26.(12分)(2019·安顺)(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE
是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC得到AB=FC,从而把AB,AD,DC转化在一个三角形中,即可判断AB,AD,DC之间的等量关系为________________;
(2)问题探究:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,点E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
检测内容:第2章 三角形(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是(
B
)
2.如图,△ABC≌△BDE,若AB=12,ED=5,则CD的长为(
C
)
A.5
B.6
C.7
D.8
3.在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠ADC的度数是(
A
)
A.107°
B.112°
C.117°
D.122°
第2题图
第4题图
第8题图
第9题图
4.(苏州中考)如图,在△ABC中,点D在边BC上,AB=AD=DC,∠B=80°,则∠C的度数为(
B
)
A.30°
B.40°
C.45°
D.60°
5.在△ABC中,∠A=∠B=∠C,则此三角形是(
B
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
6.已知不等边三角形的两边长分别是2
cm和9
cm,如果第三边的长为整数,那么第三边的长为(
C
)
A.8
cm
B.10
cm
C.8
cm或10
cm
D.8
cm或9
cm
7.下列条件中,能作出唯一三角形的是(
A
)
A.已知三边作三角形
B.已知两边及一角作三角形
C.已知两角及一边作三角形
D.已知一锐角和一直角边作直角三角形
8.如图,在△ABC中,∠A=30°,∠C=90°,AB的垂直平分线交AC于点D,交AB于点E,则下列结论错误的是(
C
)
A.AD=DB
B.∠BDE=60°
C.BC=AD
D.△ADE≌△BDC
9.如图,∠ADB=∠ACB=90°,OA=OB,且AC,BD交于点O.有下列说法:①AD=BC;②AC=BD;③∠DCA=∠CDB;④AB∥CD.其中正确的说法有(
D
)
A.1个
B.2个
C.3个
D.4个
10.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③EF=AP;④S四边形AEPF=S△ABC.当∠EPF在△ABC内绕P旋转时(点E不与A,B重合),上述结论始终正确的有(
C
)
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共24分)
11.如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.你添加的条件是__∠B=∠C(答案不唯一)__(不再添加辅助线和字母).
12.命题“互为相反数的两个数之和等于0”的逆命题是:__如果两个数之和等于0,那么这两个数互为相反数__,它是__真__命题(填“真”或“假”).
13.在△ABC中,三边的长分别为a,b,c,且满足(a-b)2+(b-c)2=0,则这个三角形一定是__等边三角形__.
14.如图,△AOB≌△DOC,△AOB的周长为10,且BC=4,则△DBC的周长为__14__.
15.(2019·江西)如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE=__20°__.
16.如图,在长方形ABCD中,把△DBC沿BD折叠得△BDC′,则图中共有__4__对全等三角形.
17.如图,AB∥CD,∠BAC与∠ACD的平分线相交于点O,OE⊥AC于点E,且OE=5
cm,则直线AB与CD之间的距离为__10__
cm.
18.如图,△ABC的面积为4
cm2,BP平分∠ABC,且AP⊥BP于点P,则△PBC的面积为__2__cm2.
三、解答题(共66分)
19.(6分)如图,已知∠MON,点A,B在OM上,点C在∠MON的平分线上,且点C到A,B两点的距离相等,用尺规作图画出点C.(不写作法,但要保留作图痕迹)
解:如图所示,点C即为所求
20.(6分)如图,AD是△ABC的角平分线,∠B=45°,点E在BC的延长线上且EH⊥AD于点H.若∠ACB=85°,求∠E的度数.
解:∵AD是△ABC的角平分线,∴∠BAD=∠CAD=∠BAC.∵∠ACB=85°,∠B=45°,且∠ACB+∠B+∠BAC=180°,∴∠BAC=50°,∴∠CAD=25°.∵∠ACB+∠CAD+∠ADC=180°,∴∠ADC=70°.∵EH⊥AD,∴∠E+∠ADC=90°,
∴∠E=90°-70°=20°
21.(6分)如图,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,请你找出图中的全等的三角形,并证明你的结论.
解:△ACD≌△BCE.证明如下:∵△ACB和△ECD都是等腰直角三角形,∴AC=BC,CD=CE,∠ACB=∠ECD=90°,∴∠ACD=∠ECB.在△ACD和△BCE中,∴△ACD≌△BCE(SAS)
22.(8分)如图所示,点D为码头,A,B为灯塔,A,B两个灯塔到码头D的距离相等,DA,DB为海岸线.一轮船离开码头,计划沿∠ADB的平分线航行.在航行途中C点处,测得轮船到灯塔A和灯塔B的距离相等.试问:轮船航行时,是否偏离了预定的航线,请说明理由.
解:轮船航行时,没有偏离航线.理由如下:由题意知DA=DB,AC=BC.在△ADC和△BDC中,∴△ADC≌△BDC(SSS),∴∠ADC=∠BDC,即DC为∠ADB的平分线,∴轮船航行时,没有偏离航线
23.(8分)王强同学用10块高度都是2
cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.
解:由题意得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,∴∠BCE=∠DAC,在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),∴AD=EC=6
cm,DC=BE=14
cm,∴DE=DC+CE=20(cm),答:两堵木墙之间的距离为20
cm
24.(10分)(2019·杭州)如图,在△ABC中,AC<AB<BC.
(1)已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B;
(2)以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连接AQ.若∠AQC=3∠B,求∠B的度数.
解:(1)证明:∵线段AB的垂直平分线与BC边交于点P,∴PA=PB,∴∠B=∠BAP,∵∠APC=∠B+∠BAP.∴∠APC=2∠B
(2)根据题意可知BA=BQ,∴∠BAQ=∠BQA.∵∠AQC=3∠B,∠AQC=∠B+∠BAQ,∴∠BQA=2∠B.∵∠BAQ+∠BQA+∠B=180°,∴5∠B=180°,∴∠B=36°
25.(10分)如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点E在线段CA上由C点向A点运动.当点E的运动速度为多少厘米/秒时,能够在某一时刻使△BPD与△CEP全等.
解:设点E运动的时间为t
s,点E运动的速度为x
cm/s,则BP=4t
cm,PC=16-4t
cm,CE=tx
cm,∵AB=AC=24
cm,∴∠B=∠C.∵点D为AB的中点,∴BD=AB=12,根据“SAS”:①当CP=BD,CE=BP时,得16-4t=12,tx=4t,解得t=1,x=4;②当CP=BP,CE=BD时,得16-4t=4t,tx=12,解得t=2,x=6,综上所述,当点E的运动速度为4厘米/秒或6厘米/秒时,能够在某一时刻使△BPD与△CEP全等
26.(12分)(2019·安顺)(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE
是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC得到AB=FC,从而把AB,AD,DC转化在一个三角形中,即可判断AB,AD,DC之间的等量关系为________________;
(2)问题探究:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,点E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
解:(1)AD=AB+DC,理由如下:∵AB∥CD,∴∠F=∠BAE.∵∠DAE=∠BAE,∴∠DAE=∠F,∴AD=DF.∵CE=BE,且∠F=∠BAE,∠AEB=∠CEF,∴△CEF≌△BEA(AAS),∴AB=CF,∴AD=CD+CF=CD+AB
(2)AB=AF+CF,理由如下:如图②,延长AE交DF的延长线于点G,∵AB∥DC,∴∠BAE=∠G.又∵BE=CE,∠AEB=∠GEC,∴△AEB≌△GEC(AAS),∴AB=GC.∵AE是∠BAF的平分线,∴∠BAG=∠FAG.∵∠BAG=∠G,∴∠FAG=∠G,∴FA=FG.∵CG=CF+FG,
∴AB=AF+CF
5
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是(
)
2.如图,△ABC≌△BDE,若AB=12,ED=5,则CD的长为(
)
A.5
B.6
C.7
D.8
3.在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠ADC的度数是(
)
A.107°
B.112°
C.117°
D.122°
第2题图
第4题图
第8题图
第9题图
4.(苏州中考)如图,在△ABC中,点D在边BC上,AB=AD=DC,∠B=80°,则∠C的度数为(
)
A.30°
B.40°
C.45°
D.60°
5.在△ABC中,∠A=∠B=∠C,则此三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
6.已知不等边三角形的两边长分别是2
cm和9
cm,如果第三边的长为整数,那么第三边的长为(
)
A.8
cm
B.10
cm
C.8
cm或10
cm
D.8
cm或9
cm
7.下列条件中,能作出唯一三角形的是(
)
A.已知三边作三角形
B.已知两边及一角作三角形
C.已知两角及一边作三角形
D.已知一锐角和一直角边作直角三角形
8.如图,在△ABC中,∠A=30°,∠C=90°,AB的垂直平分线交AC于点D,交AB于点E,则下列结论错误的是(
)
A.AD=DB
B.∠BDE=60°
C.BC=AD
D.△ADE≌△BDC
9.如图,∠ADB=∠ACB=90°,OA=OB,且AC,BD交于点O.有下列说法:①AD=BC;②AC=BD;③∠DCA=∠CDB;④AB∥CD.其中正确的说法有(
)
A.1个
B.2个
C.3个
D.4个
10.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③EF=AP;④S四边形AEPF=S△ABC.当∠EPF在△ABC内绕P旋转时(点E不与A,B重合),上述结论始终正确的有(
)
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共24分)
11.如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.你添加的条件是________________
(不再添加辅助线和字母).
12.命题“互为相反数的两个数之和等于0”的逆命题是:___________________________________________________,它是________________命题(填“真”或“假”).
13.在△ABC中,三边的长分别为a,b,c,且满足(a-b)2+(b-c)2=0,则这个三角形一定是________________.
14.如图,△AOB≌△DOC,△AOB的周长为10,且BC=4,则△DBC的周长为________________.
15.(2019·江西)如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE=________________.
16.如图,在长方形ABCD中,把△DBC沿BD折叠得△BDC′,则图中共有________________对全等三角形.
17.如图,AB∥CD,∠BAC与∠ACD的平分线相交于点O,OE⊥AC于点E,且OE=5
cm,则直线AB与CD之间的距离为________________
cm.
18.如图,△ABC的面积为4
cm2,BP平分∠ABC,且AP⊥BP于点P,则△PBC的面积为________________cm2.
三、解答题(共66分)
19.(6分)如图,已知∠MON,点A,B在OM上,点C在∠MON的平分线上,且点C到A,B两点的距离相等,用尺规作图画出点C.(不写作法,但要保留作图痕迹)
20.(6分)如图,AD是△ABC的角平分线,∠B=45°,点E在BC的延长线上且EH⊥AD于点H.若∠ACB=85°,求∠E的度数.
21.(6分)如图,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,请你找出图中的全等的三角形,并证明你的结论.
22.(8分)如图所示,点D为码头,A,B为灯塔,A,B两个灯塔到码头D的距离相等,DA,DB为海岸线.一轮船离开码头,计划沿∠ADB的平分线航行.在航行途中C点处,测得轮船到灯塔A和灯塔B的距离相等.试问:轮船航行时,是否偏离了预定的航线,请说明理由.
23.(8分)王强同学用10块高度都是2
cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.
24.(10分)(2019·杭州)如图,在△ABC中,AC<AB<BC.
(1)已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B;
(2)以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连接AQ.若∠AQC=3∠B,求∠B的度数.
25.(10分)如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点E在线段CA上由C点向A点运动.当点E的运动速度为多少厘米/秒时,能够在某一时刻使△BPD与△CEP全等.
26.(12分)(2019·安顺)(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE
是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC得到AB=FC,从而把AB,AD,DC转化在一个三角形中,即可判断AB,AD,DC之间的等量关系为________________;
(2)问题探究:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,点E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
检测内容:第2章 三角形(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是(
B
)
2.如图,△ABC≌△BDE,若AB=12,ED=5,则CD的长为(
C
)
A.5
B.6
C.7
D.8
3.在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠ADC的度数是(
A
)
A.107°
B.112°
C.117°
D.122°
第2题图
第4题图
第8题图
第9题图
4.(苏州中考)如图,在△ABC中,点D在边BC上,AB=AD=DC,∠B=80°,则∠C的度数为(
B
)
A.30°
B.40°
C.45°
D.60°
5.在△ABC中,∠A=∠B=∠C,则此三角形是(
B
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
6.已知不等边三角形的两边长分别是2
cm和9
cm,如果第三边的长为整数,那么第三边的长为(
C
)
A.8
cm
B.10
cm
C.8
cm或10
cm
D.8
cm或9
cm
7.下列条件中,能作出唯一三角形的是(
A
)
A.已知三边作三角形
B.已知两边及一角作三角形
C.已知两角及一边作三角形
D.已知一锐角和一直角边作直角三角形
8.如图,在△ABC中,∠A=30°,∠C=90°,AB的垂直平分线交AC于点D,交AB于点E,则下列结论错误的是(
C
)
A.AD=DB
B.∠BDE=60°
C.BC=AD
D.△ADE≌△BDC
9.如图,∠ADB=∠ACB=90°,OA=OB,且AC,BD交于点O.有下列说法:①AD=BC;②AC=BD;③∠DCA=∠CDB;④AB∥CD.其中正确的说法有(
D
)
A.1个
B.2个
C.3个
D.4个
10.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③EF=AP;④S四边形AEPF=S△ABC.当∠EPF在△ABC内绕P旋转时(点E不与A,B重合),上述结论始终正确的有(
C
)
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共24分)
11.如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.你添加的条件是__∠B=∠C(答案不唯一)__(不再添加辅助线和字母).
12.命题“互为相反数的两个数之和等于0”的逆命题是:__如果两个数之和等于0,那么这两个数互为相反数__,它是__真__命题(填“真”或“假”).
13.在△ABC中,三边的长分别为a,b,c,且满足(a-b)2+(b-c)2=0,则这个三角形一定是__等边三角形__.
14.如图,△AOB≌△DOC,△AOB的周长为10,且BC=4,则△DBC的周长为__14__.
15.(2019·江西)如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE=__20°__.
16.如图,在长方形ABCD中,把△DBC沿BD折叠得△BDC′,则图中共有__4__对全等三角形.
17.如图,AB∥CD,∠BAC与∠ACD的平分线相交于点O,OE⊥AC于点E,且OE=5
cm,则直线AB与CD之间的距离为__10__
cm.
18.如图,△ABC的面积为4
cm2,BP平分∠ABC,且AP⊥BP于点P,则△PBC的面积为__2__cm2.
三、解答题(共66分)
19.(6分)如图,已知∠MON,点A,B在OM上,点C在∠MON的平分线上,且点C到A,B两点的距离相等,用尺规作图画出点C.(不写作法,但要保留作图痕迹)
解:如图所示,点C即为所求
20.(6分)如图,AD是△ABC的角平分线,∠B=45°,点E在BC的延长线上且EH⊥AD于点H.若∠ACB=85°,求∠E的度数.
解:∵AD是△ABC的角平分线,∴∠BAD=∠CAD=∠BAC.∵∠ACB=85°,∠B=45°,且∠ACB+∠B+∠BAC=180°,∴∠BAC=50°,∴∠CAD=25°.∵∠ACB+∠CAD+∠ADC=180°,∴∠ADC=70°.∵EH⊥AD,∴∠E+∠ADC=90°,
∴∠E=90°-70°=20°
21.(6分)如图,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,请你找出图中的全等的三角形,并证明你的结论.
解:△ACD≌△BCE.证明如下:∵△ACB和△ECD都是等腰直角三角形,∴AC=BC,CD=CE,∠ACB=∠ECD=90°,∴∠ACD=∠ECB.在△ACD和△BCE中,∴△ACD≌△BCE(SAS)
22.(8分)如图所示,点D为码头,A,B为灯塔,A,B两个灯塔到码头D的距离相等,DA,DB为海岸线.一轮船离开码头,计划沿∠ADB的平分线航行.在航行途中C点处,测得轮船到灯塔A和灯塔B的距离相等.试问:轮船航行时,是否偏离了预定的航线,请说明理由.
解:轮船航行时,没有偏离航线.理由如下:由题意知DA=DB,AC=BC.在△ADC和△BDC中,∴△ADC≌△BDC(SSS),∴∠ADC=∠BDC,即DC为∠ADB的平分线,∴轮船航行时,没有偏离航线
23.(8分)王强同学用10块高度都是2
cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.
解:由题意得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,∴∠BCE=∠DAC,在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),∴AD=EC=6
cm,DC=BE=14
cm,∴DE=DC+CE=20(cm),答:两堵木墙之间的距离为20
cm
24.(10分)(2019·杭州)如图,在△ABC中,AC<AB<BC.
(1)已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B;
(2)以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连接AQ.若∠AQC=3∠B,求∠B的度数.
解:(1)证明:∵线段AB的垂直平分线与BC边交于点P,∴PA=PB,∴∠B=∠BAP,∵∠APC=∠B+∠BAP.∴∠APC=2∠B
(2)根据题意可知BA=BQ,∴∠BAQ=∠BQA.∵∠AQC=3∠B,∠AQC=∠B+∠BAQ,∴∠BQA=2∠B.∵∠BAQ+∠BQA+∠B=180°,∴5∠B=180°,∴∠B=36°
25.(10分)如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点E在线段CA上由C点向A点运动.当点E的运动速度为多少厘米/秒时,能够在某一时刻使△BPD与△CEP全等.
解:设点E运动的时间为t
s,点E运动的速度为x
cm/s,则BP=4t
cm,PC=16-4t
cm,CE=tx
cm,∵AB=AC=24
cm,∴∠B=∠C.∵点D为AB的中点,∴BD=AB=12,根据“SAS”:①当CP=BD,CE=BP时,得16-4t=12,tx=4t,解得t=1,x=4;②当CP=BP,CE=BD时,得16-4t=4t,tx=12,解得t=2,x=6,综上所述,当点E的运动速度为4厘米/秒或6厘米/秒时,能够在某一时刻使△BPD与△CEP全等
26.(12分)(2019·安顺)(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE
是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC得到AB=FC,从而把AB,AD,DC转化在一个三角形中,即可判断AB,AD,DC之间的等量关系为________________;
(2)问题探究:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,点E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
解:(1)AD=AB+DC,理由如下:∵AB∥CD,∴∠F=∠BAE.∵∠DAE=∠BAE,∴∠DAE=∠F,∴AD=DF.∵CE=BE,且∠F=∠BAE,∠AEB=∠CEF,∴△CEF≌△BEA(AAS),∴AB=CF,∴AD=CD+CF=CD+AB
(2)AB=AF+CF,理由如下:如图②,延长AE交DF的延长线于点G,∵AB∥DC,∴∠BAE=∠G.又∵BE=CE,∠AEB=∠GEC,∴△AEB≌△GEC(AAS),∴AB=GC.∵AE是∠BAF的平分线,∴∠BAG=∠FAG.∵∠BAG=∠G,∴∠FAG=∠G,∴FA=FG.∵CG=CF+FG,
∴AB=AF+CF
5
同课章节目录
