人教新课标数学六年级下册《成正比例的量 3》ppt课件
文档属性
| 名称 | 人教新课标数学六年级下册《成正比例的量 3》ppt课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-24 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
成正比例的量
教学目标
1. 理解成正比例的意义,能正确判断两种量是否成正比例。
2. 培养同学们分析、归纳、判断能力。
3. 渗透函数思想,进行辨证唯物主义的启蒙教育。
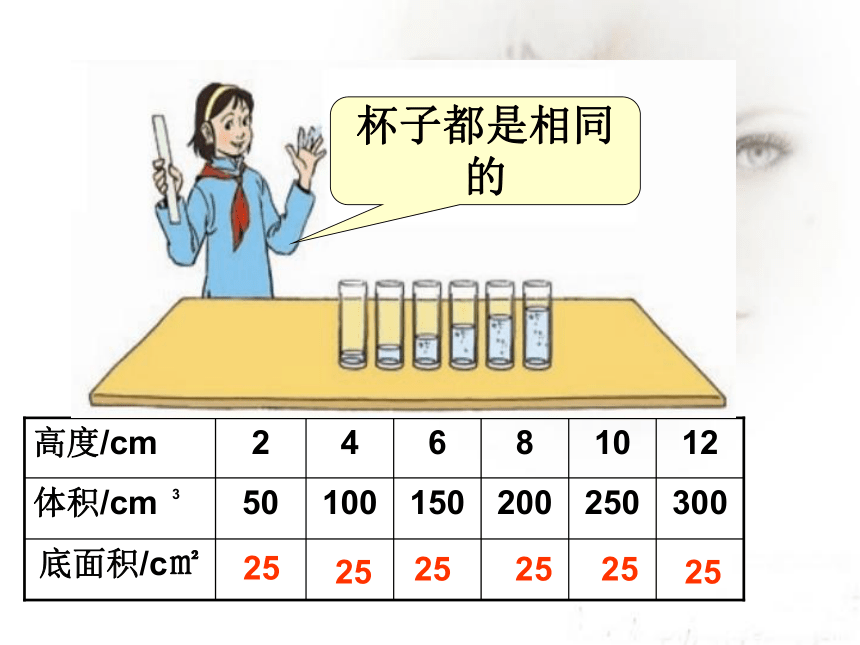
底面积/c㎡
300
250
200
150
100
50
体积/cm
12
10
8
6
4
2
高度/cm
3
25
25
25
25
25
25
杯子都是相同的
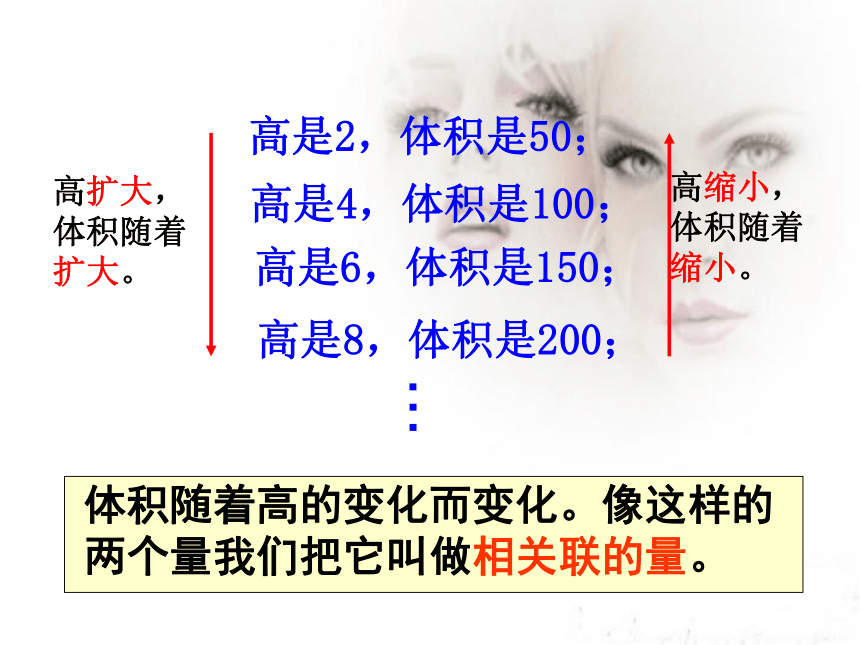
高是2,体积是50;
高是4,体积是100;
高是6,体积是150;
高是8,体积是200;
高扩大,
体积随着
扩大。
高缩小,
体积随着
缩小。
体积随着高的变化而变化。像这样的两个量我们把它叫做相关联的量。
体积和高的比值:
50
2
=25
100
4
=25
150
6
=25
…
(1)水的体积随着高度的变化而变化;
(2)水的高度增加,体积随着增加;水的高度降低,体积也随着减少;
(3)体积和高的比值都是25。
体积和高的比值:
50
2
=25
100
4
=25
150
6
=25
…
体积
高
=底面积
(一定)
两种量,一种量变化,另一种量也随着变化,而且这两种量的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
体积
高
=底面积
(一定)
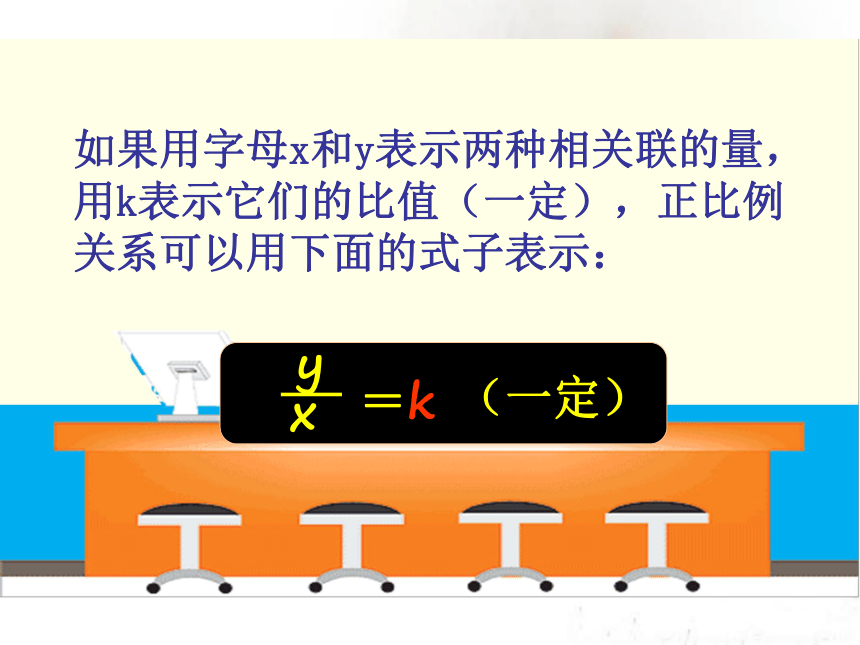
y
x
=k
(一定)
如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
判定方法:
判定两个量是不是成正比例,主
要是看它们的商是不是一定的。
我的收获
1.判定两个量是否成正比例,
主要看它们的( )是否一定。
2.苹果的单价一定,苹果的数量和总价。( )和( )是相关联的量。
所以( )和( )是成正比例的量。
( )
( )
=( )(一定)
底面积/c㎡
300
250
200
150
100
50
体积/cm
12
10
8
6
4
2
高度/cm
3
25
25
25
25
25
25
把实验结果用图像表示
2 4 6 8 10 12 14
300
250
200
150
100
50
0
体积/cm
3
高度/cm
(1) 从图中你发现了什么
(2) 不计算,根据图像判断,如果杯中 水的高度是7cm,那么水的体积是多少 225立方厘米的水有多高
一辆汽车行驶的时间和所行路程如下表。
时间(时)
路程(千米)
1
80
2
160
3
240
4
320
5
400
6
480
7
560
…
…
(1)写出几组路程和相对应的时间的比,并比
较比值的大小。说一说这个比值表示什么。
(2)表中的路程和时间成正比例吗?为什么
(3)在图中描出表示路程和相应时间的点,然后
把它们按顺序连起来。并估计下行驶120km
大约要用多长时间。
1 2 3 4 5 6 7
480
400
320
240
160
80
0
路程/km
时间/时
长方形的宽一定,长和它的面积。
长
轮船行驶的速度一定,行驶的路程和时间。
判断下面每题中的两种量是不是成正比例,并说明理由。
苹果的单价一定,购买苹果的数量和总价。
小新跳高的高度和他的身高。
小麦每公顷的产量一定,小麦的公顷数和总产量。
矿泉水瓶中喝掉的水和剩下的水。
圆的半径和它的面积。
r
成正比例的量
教学目标
1. 理解成正比例的意义,能正确判断两种量是否成正比例。
2. 培养同学们分析、归纳、判断能力。
3. 渗透函数思想,进行辨证唯物主义的启蒙教育。
底面积/c㎡
300
250
200
150
100
50
体积/cm
12
10
8
6
4
2
高度/cm
3
25
25
25
25
25
25
杯子都是相同的
高是2,体积是50;
高是4,体积是100;
高是6,体积是150;
高是8,体积是200;
高扩大,
体积随着
扩大。
高缩小,
体积随着
缩小。
体积随着高的变化而变化。像这样的两个量我们把它叫做相关联的量。
体积和高的比值:
50
2
=25
100
4
=25
150
6
=25
…
(1)水的体积随着高度的变化而变化;
(2)水的高度增加,体积随着增加;水的高度降低,体积也随着减少;
(3)体积和高的比值都是25。
体积和高的比值:
50
2
=25
100
4
=25
150
6
=25
…
体积
高
=底面积
(一定)
两种量,一种量变化,另一种量也随着变化,而且这两种量的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
体积
高
=底面积
(一定)
y
x
=k
(一定)
如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
判定方法:
判定两个量是不是成正比例,主
要是看它们的商是不是一定的。
我的收获
1.判定两个量是否成正比例,
主要看它们的( )是否一定。
2.苹果的单价一定,苹果的数量和总价。( )和( )是相关联的量。
所以( )和( )是成正比例的量。
( )
( )
=( )(一定)
底面积/c㎡
300
250
200
150
100
50
体积/cm
12
10
8
6
4
2
高度/cm
3
25
25
25
25
25
25
把实验结果用图像表示
2 4 6 8 10 12 14
300
250
200
150
100
50
0
体积/cm
3
高度/cm
(1) 从图中你发现了什么
(2) 不计算,根据图像判断,如果杯中 水的高度是7cm,那么水的体积是多少 225立方厘米的水有多高
一辆汽车行驶的时间和所行路程如下表。
时间(时)
路程(千米)
1
80
2
160
3
240
4
320
5
400
6
480
7
560
…
…
(1)写出几组路程和相对应的时间的比,并比
较比值的大小。说一说这个比值表示什么。
(2)表中的路程和时间成正比例吗?为什么
(3)在图中描出表示路程和相应时间的点,然后
把它们按顺序连起来。并估计下行驶120km
大约要用多长时间。
1 2 3 4 5 6 7
480
400
320
240
160
80
0
路程/km
时间/时
长方形的宽一定,长和它的面积。
长
轮船行驶的速度一定,行驶的路程和时间。
判断下面每题中的两种量是不是成正比例,并说明理由。
苹果的单价一定,购买苹果的数量和总价。
小新跳高的高度和他的身高。
小麦每公顷的产量一定,小麦的公顷数和总产量。
矿泉水瓶中喝掉的水和剩下的水。
圆的半径和它的面积。
r
