教科版(2019)高中信息技术必修一 4.1算法及特征 课件(21张ppt)
文档属性
| 名称 | 教科版(2019)高中信息技术必修一 4.1算法及特征 课件(21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 824.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2020-09-08 00:00:00 | ||
图片预览







文档简介
第4单元计算与问题解决
人类必将生活在一种程序设计的世界里。在这个世界里,人类文化与程序设计不仅并行存在,而且会互相联系,融合为一种全新的人类思想。 ——叶尔肖夫 ( Yershow)
计算科学是关于计算的学问,它主要研究哪些问题是可计算的以及怎样去计算。计算是获得信息的一种过程,所以计算是动态的,信息的获得是计算的延伸。可以说,问题解决的过程,实质上是描述和变换信息的过程。
本单元我们将对“计算”进行更多探究。我们将进一步了解计算与算法的关系,明确算法的基本特征,尝试用枚举的思想实现简单算法;掌握数值类及非数值类问题求解中的常用算法思想;学会分析问题,针对问题的解决选择合理的算法,运用已学的计算知识解决实际问题。
4.1 算法及特征
算法并不遥远,它就在我们身边。日常生活中,很多看似平常的做法都蕴含着一定的道理,如果将这些做法抽象成数学描述可能就是一些非常有效的算法。算法可能是一个计算公式,可能是一个赢得游戏的策略,也可能是一个解决综合问题的复杂方案。
学习目标
★熟悉将解决问题的方法归结为一系列清晰、 准确的步骤的过程。
★了解算法的基本要素和重要特征。
★运用恰当的方式描述算法。
★运用Python语言实现简单算法,解决问题。
新知导入
软件设计师是业务领域和技术领城的专家。面对客户需求,软件设计师要对问题进行整体分析以找到解决方案,通过恰当的方式与客户沟通;面对技术问题,软件设计师需要借助计算机编程解决实际问题。我们将通过“软件开发社招新”项目讨论计算机编程解决问题的过程。
本项目主要包含“探讨面试题的解决方案”和“求解‘谁是冠军’”两个任务。
任务一 探讨面试题的解决方案
※活动1寻找 “开关对应关系”
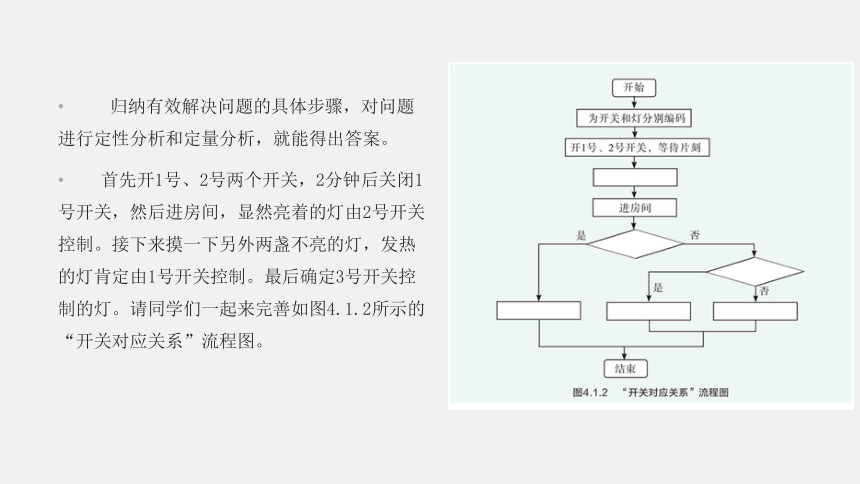
软件开发社团要招募新成员,报名的同学要经过面试才能加入。第一关面试题是: “一个房间有3盏灯,房间外有3个开关分别控制这3盏灯,如图4.1.1所示。在只允许进房间一次的情况下,如何判断哪个开关控制哪盏灯?”
设计算法是解决问题的核心,它的基本任务是对问题进行定性分析和定量分析,遵循算法的特征和约定,寻求计算的方法和规则,明确解决问题的途径。
从表面上看,灯只有亮、灭两种状态,但是灯又具有一种特殊性,即开灯的同时会伴随发光发热,因此灯被触摸时还有冷、热两种状态。综上所述,一盏灯可能有4种不同的状态。而在房间内共有3盏灯,完全可以保证每盏灯的状态都是唯一的。由于题目中并没有限制开关按动次数,所以3个开关的闭合状态是可以随意改变的。如何能使3盏灯处于不同的状态?
请在下框中写下你的步骤,在小组中比比谁的方法更快捷、更合理。
第一步:
第二步:
......
归纳有效解决问题的具体步骤,对问题进行定性分析和定量分析,就能得出答案。
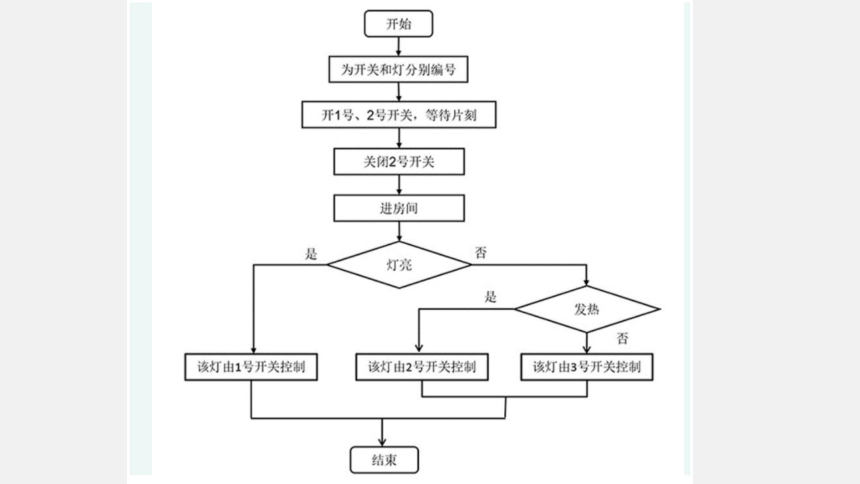
首先开1号、2号两个开关,2分钟后关闭1号开关,然后进房间,显然亮着的灯由2号开关控制。接下来摸一下另外两盏不亮的灯,发热的灯肯定由1号开关控制。最后确定3号开关控制的灯。请同学们一起来完善如图4.1.2所示的“开关对应关系”流程图。
算法的重要特征
有穷性。算法必须能在执行有限个步骤之后终止。
确切性。算法中的每一次运算都有明确的定义,具有无二义性,并且可以通过计算得到唯一的结果。
输入项。一个算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输人是指算法本身给出了初始条 件。
输出项。算法一定要有输出。任何算法都不能“无功而返”。
可行性。算法中执行的任何计算都可以在有限时间内完成(也称为有效性)。算法中的运算都必须是可以实现的。
从某种意义上说,算法也是一种数学模型。一般而言,问题求解的第一步是数学建模。用数学语言描述实际现象,将现实世界的问题抽象成数学模型,就可能发现问题的本质并判定其能否求解,继而找到求解该问题的方法和算法。
※活动2定量分析, 寻找“被污染的药丸”
面试的第二关是实验题。如图4.1.3所示, 有4个分别装了4种药丸的药瓶,里面每颗药丸都有单颗标准质量,其中有一个药瓶中的所有药丸都被污染了。每颗被污染的要玩比正常的药丸增重1g,请只允许城中一次的情况下,判断哪个药瓶中的药丸被污染了。
如果从每个药瓶中取出1颗药丸分别进行称重,肯定可以判断出哪颗药丸被污染了,但是这种做法显然不符合“只能称量一次”的要求。你能改进判断方法吗?
活动2定量分析, 寻找“被污染的药丸”
考虑1颗药丸的重量变化,如果药丸被污染,则增重____克, 否则增重____克。
从某一个药瓶中取出n颗药丸,如果被污染,则增重 克,否则增重___克。
如果我们从不同的药瓶中取出不同颗数的药丸,你能根据增重情况找出被污染的药丸吗?
从第1个药瓶中取出1颗药丸,从第2个药瓶中取出2颗药丸,从第3个药瓶中取出3颗药丸,从第4个药瓶中取出4颗药丸,共10颗药丸。
如果增重____克, 则____ 号 药瓶中的药丸被污染。
回顾算法的特点,思考一下,在这个问题中,哪些信息属于输入、哪些信息属于输出呢?
请设计程序并运行,使输入10颗药丸的总重量及4种药丸的单颗标准质量就可以看到结果,找到被污染的药丸。
d=int(input('请输入每颗药丸的标准重量:'))
w=int(input('请输入药丸称得的重量:'))
x=w-10*d
print('被污染的药瓶序号是:',x)
input("运行完毕,请按回车键退出...")
※活动3巧用运算, 寻找“误删的ID号”
面试的第三关是程序设计题。学校历届校友的数据存储在学校网络中心服务器中(共10000条,无重复数据),某管理员由于误操作删除了一位校友的ID号(8位整数)。恰好在备份文件中保存了所有人员的ID号(无重复数据,无序)。怎样快速找出被误删的ID号以便恢复数据?仔细分析问题,我们发现实际需要参与分析及处理的只有ID号,而且这些ID号的特征也很明显。请归纳ID号的特征,写在下面的横线上。
D号的特征
①数据类型及大小范围:
②数据在两个文件中出现的次数:
③备份文件中ID号总和与故障文件中的ID号总和的差值为:
target=0 #设置初始值
f1=open("copy.txt","r") #打开备份文件
list1=f1.readlines() #读取每行数据
for line in list1:
target=target+int(line) #将读取的数据做和运算
f1.close() #关闭备份文件
f2=open("trouble.txt","r") #打开故障文件
list2=f2.readlines() #读取每行数据
for line in list2:
target=target-int(line) #将读取的数据做减运算
f2.close() #关闭故障文件
print("被删除的ID号是:",target) #输出被删除的ID号
input("运行完毕,请按回车键退出...")
运行效果
文件打开模式
任务二 求解谁是冠军
※活动尝试枚举
这次面试的冠军在A、B、C、D四位同学中。
A说:不是我。
B说:是C。
C说:是D。
D说:C说的不对。
已知四人中有一人说了假话。你能判断出到底谁是冠军吗?说出你的结论和判断过程。
枚举
champion=['A','B','C','D'] #设置选手列表
for i in champion: #循环读取选手编号
cond=(i!='A') +(i=='C') + (i=='D')+(i!='D') #查找符合条件的选手
if cond==3: #说真话是否是3人
print("冠军是:",i) #输出冠军
input("运行完毕,请按回车键退出...")
●枚举
我们常利用计算机运算速度快、精确度高的特点解决实际问题。在设计算法时,最简单的方法就是“直译”我们的思维过程。有一种算法是把所有可能的答案一一列举, 合适就保留,不合适就丢弃。这种方法
称作“枚举”或“穷举”
在不知道谁说真话、谁说假话的情况下,最简单的方法就是把所有可能都枚举出来。因为只有一位冠军,所以可以枚举选手的编号,并对A、B、C、D四个人的话进行判断。
计算的本质是完成一系列算术运算和逻辑运算。因此在进行计算时,首先要将各种类型的数值问题转化为计算机能够执行的基本运算。在本任务中,我们需要把每个人说的话转化成计算机能够执行的表达式。如A说:“不是我。 ”可以表示为i!=“A”, 其中i为枚举的冠军选手编号。
请分析以下代码的含义,理解解题思路,并在横线上填写语句的功能。
华容道
1、历经中外科学家姜长英、藤村幸三郎、清水达雄、马丁加达纳等几十年的努力,游戏解法已由六十多年前的87步减少至81步。
2、美国一个律师托马斯.莱曼(Thomas B.Lenann)发现一个新的解法,由加德纳公布在1964年3月《科学美国人》上,有81步,称加德纳解法。
3、华容道的最快走法在中国是100步,在日本是82步。后来美国人用计算机,使用穷举法找出了最终解法,不可能有再快的解法了,81步。美国人在用计算机找到最终解法后,跟中国人开玩笑说美国一位著名的博士找到了最终解法,这位博士名叫computer。
人类必将生活在一种程序设计的世界里。在这个世界里,人类文化与程序设计不仅并行存在,而且会互相联系,融合为一种全新的人类思想。 ——叶尔肖夫 ( Yershow)
计算科学是关于计算的学问,它主要研究哪些问题是可计算的以及怎样去计算。计算是获得信息的一种过程,所以计算是动态的,信息的获得是计算的延伸。可以说,问题解决的过程,实质上是描述和变换信息的过程。
本单元我们将对“计算”进行更多探究。我们将进一步了解计算与算法的关系,明确算法的基本特征,尝试用枚举的思想实现简单算法;掌握数值类及非数值类问题求解中的常用算法思想;学会分析问题,针对问题的解决选择合理的算法,运用已学的计算知识解决实际问题。
4.1 算法及特征
算法并不遥远,它就在我们身边。日常生活中,很多看似平常的做法都蕴含着一定的道理,如果将这些做法抽象成数学描述可能就是一些非常有效的算法。算法可能是一个计算公式,可能是一个赢得游戏的策略,也可能是一个解决综合问题的复杂方案。
学习目标
★熟悉将解决问题的方法归结为一系列清晰、 准确的步骤的过程。
★了解算法的基本要素和重要特征。
★运用恰当的方式描述算法。
★运用Python语言实现简单算法,解决问题。
新知导入
软件设计师是业务领域和技术领城的专家。面对客户需求,软件设计师要对问题进行整体分析以找到解决方案,通过恰当的方式与客户沟通;面对技术问题,软件设计师需要借助计算机编程解决实际问题。我们将通过“软件开发社招新”项目讨论计算机编程解决问题的过程。
本项目主要包含“探讨面试题的解决方案”和“求解‘谁是冠军’”两个任务。
任务一 探讨面试题的解决方案
※活动1寻找 “开关对应关系”
软件开发社团要招募新成员,报名的同学要经过面试才能加入。第一关面试题是: “一个房间有3盏灯,房间外有3个开关分别控制这3盏灯,如图4.1.1所示。在只允许进房间一次的情况下,如何判断哪个开关控制哪盏灯?”
设计算法是解决问题的核心,它的基本任务是对问题进行定性分析和定量分析,遵循算法的特征和约定,寻求计算的方法和规则,明确解决问题的途径。
从表面上看,灯只有亮、灭两种状态,但是灯又具有一种特殊性,即开灯的同时会伴随发光发热,因此灯被触摸时还有冷、热两种状态。综上所述,一盏灯可能有4种不同的状态。而在房间内共有3盏灯,完全可以保证每盏灯的状态都是唯一的。由于题目中并没有限制开关按动次数,所以3个开关的闭合状态是可以随意改变的。如何能使3盏灯处于不同的状态?
请在下框中写下你的步骤,在小组中比比谁的方法更快捷、更合理。
第一步:
第二步:
......
归纳有效解决问题的具体步骤,对问题进行定性分析和定量分析,就能得出答案。
首先开1号、2号两个开关,2分钟后关闭1号开关,然后进房间,显然亮着的灯由2号开关控制。接下来摸一下另外两盏不亮的灯,发热的灯肯定由1号开关控制。最后确定3号开关控制的灯。请同学们一起来完善如图4.1.2所示的“开关对应关系”流程图。
算法的重要特征
有穷性。算法必须能在执行有限个步骤之后终止。
确切性。算法中的每一次运算都有明确的定义,具有无二义性,并且可以通过计算得到唯一的结果。
输入项。一个算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输人是指算法本身给出了初始条 件。
输出项。算法一定要有输出。任何算法都不能“无功而返”。
可行性。算法中执行的任何计算都可以在有限时间内完成(也称为有效性)。算法中的运算都必须是可以实现的。
从某种意义上说,算法也是一种数学模型。一般而言,问题求解的第一步是数学建模。用数学语言描述实际现象,将现实世界的问题抽象成数学模型,就可能发现问题的本质并判定其能否求解,继而找到求解该问题的方法和算法。
※活动2定量分析, 寻找“被污染的药丸”
面试的第二关是实验题。如图4.1.3所示, 有4个分别装了4种药丸的药瓶,里面每颗药丸都有单颗标准质量,其中有一个药瓶中的所有药丸都被污染了。每颗被污染的要玩比正常的药丸增重1g,请只允许城中一次的情况下,判断哪个药瓶中的药丸被污染了。
如果从每个药瓶中取出1颗药丸分别进行称重,肯定可以判断出哪颗药丸被污染了,但是这种做法显然不符合“只能称量一次”的要求。你能改进判断方法吗?
活动2定量分析, 寻找“被污染的药丸”
考虑1颗药丸的重量变化,如果药丸被污染,则增重____克, 否则增重____克。
从某一个药瓶中取出n颗药丸,如果被污染,则增重 克,否则增重___克。
如果我们从不同的药瓶中取出不同颗数的药丸,你能根据增重情况找出被污染的药丸吗?
从第1个药瓶中取出1颗药丸,从第2个药瓶中取出2颗药丸,从第3个药瓶中取出3颗药丸,从第4个药瓶中取出4颗药丸,共10颗药丸。
如果增重____克, 则____ 号 药瓶中的药丸被污染。
回顾算法的特点,思考一下,在这个问题中,哪些信息属于输入、哪些信息属于输出呢?
请设计程序并运行,使输入10颗药丸的总重量及4种药丸的单颗标准质量就可以看到结果,找到被污染的药丸。
d=int(input('请输入每颗药丸的标准重量:'))
w=int(input('请输入药丸称得的重量:'))
x=w-10*d
print('被污染的药瓶序号是:',x)
input("运行完毕,请按回车键退出...")
※活动3巧用运算, 寻找“误删的ID号”
面试的第三关是程序设计题。学校历届校友的数据存储在学校网络中心服务器中(共10000条,无重复数据),某管理员由于误操作删除了一位校友的ID号(8位整数)。恰好在备份文件中保存了所有人员的ID号(无重复数据,无序)。怎样快速找出被误删的ID号以便恢复数据?仔细分析问题,我们发现实际需要参与分析及处理的只有ID号,而且这些ID号的特征也很明显。请归纳ID号的特征,写在下面的横线上。
D号的特征
①数据类型及大小范围:
②数据在两个文件中出现的次数:
③备份文件中ID号总和与故障文件中的ID号总和的差值为:
target=0 #设置初始值
f1=open("copy.txt","r") #打开备份文件
list1=f1.readlines() #读取每行数据
for line in list1:
target=target+int(line) #将读取的数据做和运算
f1.close() #关闭备份文件
f2=open("trouble.txt","r") #打开故障文件
list2=f2.readlines() #读取每行数据
for line in list2:
target=target-int(line) #将读取的数据做减运算
f2.close() #关闭故障文件
print("被删除的ID号是:",target) #输出被删除的ID号
input("运行完毕,请按回车键退出...")
运行效果
文件打开模式
任务二 求解谁是冠军
※活动尝试枚举
这次面试的冠军在A、B、C、D四位同学中。
A说:不是我。
B说:是C。
C说:是D。
D说:C说的不对。
已知四人中有一人说了假话。你能判断出到底谁是冠军吗?说出你的结论和判断过程。
枚举
champion=['A','B','C','D'] #设置选手列表
for i in champion: #循环读取选手编号
cond=(i!='A') +(i=='C') + (i=='D')+(i!='D') #查找符合条件的选手
if cond==3: #说真话是否是3人
print("冠军是:",i) #输出冠军
input("运行完毕,请按回车键退出...")
●枚举
我们常利用计算机运算速度快、精确度高的特点解决实际问题。在设计算法时,最简单的方法就是“直译”我们的思维过程。有一种算法是把所有可能的答案一一列举, 合适就保留,不合适就丢弃。这种方法
称作“枚举”或“穷举”
在不知道谁说真话、谁说假话的情况下,最简单的方法就是把所有可能都枚举出来。因为只有一位冠军,所以可以枚举选手的编号,并对A、B、C、D四个人的话进行判断。
计算的本质是完成一系列算术运算和逻辑运算。因此在进行计算时,首先要将各种类型的数值问题转化为计算机能够执行的基本运算。在本任务中,我们需要把每个人说的话转化成计算机能够执行的表达式。如A说:“不是我。 ”可以表示为i!=“A”, 其中i为枚举的冠军选手编号。
请分析以下代码的含义,理解解题思路,并在横线上填写语句的功能。
华容道
1、历经中外科学家姜长英、藤村幸三郎、清水达雄、马丁加达纳等几十年的努力,游戏解法已由六十多年前的87步减少至81步。
2、美国一个律师托马斯.莱曼(Thomas B.Lenann)发现一个新的解法,由加德纳公布在1964年3月《科学美国人》上,有81步,称加德纳解法。
3、华容道的最快走法在中国是100步,在日本是82步。后来美国人用计算机,使用穷举法找出了最终解法,不可能有再快的解法了,81步。美国人在用计算机找到最终解法后,跟中国人开玩笑说美国一位著名的博士找到了最终解法,这位博士名叫computer。
