华东师大版八年级数学上册 第13章全等三角形(word版,含答案)
文档属性
| 名称 | 华东师大版八年级数学上册 第13章全等三角形(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 496.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 17:50:15 | ||
图片预览


文档简介
检测内容:全等三角形
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.下列语句不是命题的是(
)
A.绝对值相等的两个数也相等
B.作∠AOB的平分线
C.同角的补角相等
D.长方形是轴对称图形
2.根据下列条件画三角形,不能确定唯一三角形的是(
)
A.已知三个角
B.已知三边
C.已知两角和夹边
D.已知两边和夹角
3.下列命题是假命题的有(
)
①若a2=b2,则a=b;②一个角的余角大于这个角;③若a,b是有理数,则|a+b|=|a|+|b|;④如果∠A=∠B,那么∠A与∠B是对顶角.
A.1个
B.2个
C.3个
D.4个
4.如图,已知AB=AC,AD=AE,则下列结论正确的是(
)
①EB=DC;②△BPE≌△CPD;③点P在∠BAC的平分线上.
A.①
B.②
C.①②
D.①②③
5.如图,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=(
)
A.50°
B.100°
C.120°
D.130°
6.等腰△ABC的一个外角为110°,则此等腰三角形的顶角的度数为(
)
A.40°
B.70°
C.40°或70°
D.以上都不对
7.(2020·陕西模拟)如图,已知△ABC的面积为8,在BC上截取BD=BA,作∠ABC的平分线交AD于点P,连接PC,则△BPC的面积为(
)
A.2
B.4
C.5
D.6
8.(2020·河南模拟)如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若AD=AC,∠A=80°,则∠ACB的度数为(
)
A.65°
B.70°
C.75°
D.80°
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是(
)
A.8
B.6
C.4
D.2
10.(2019·滨州)如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连结OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为(
)
A.4个
B.3个
C.2个
D.1个
二、填空题(每小题3分,共15分)
11.命题“如果两直线都和第三条直线互相平行,那么这两直线也互相平行”的逆命题是(
).
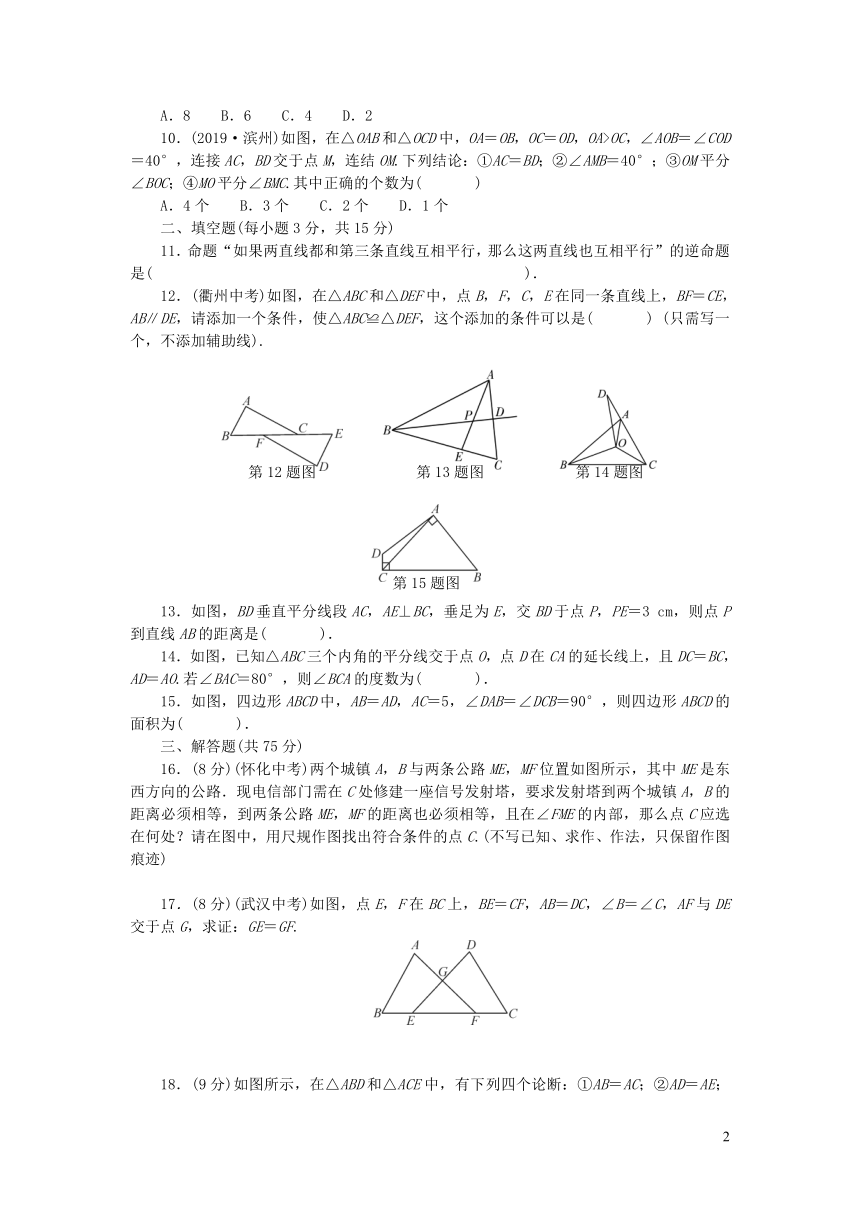
12.(衢州中考)如图,在△ABC和△DEF中,点B,F,C,E在同一条直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是(
)
(只需写一个,不添加辅助线).
13.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于点P,PE=3
cm,则点P到直线AB的距离是(
).
14.如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO.若∠BAC=80°,则∠BCA的度数为(
).
15.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为(
).
三、解答题(共75分)
16.(8分)(怀化中考)两个城镇A,B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A,B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部,那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
17.(8分)(武汉中考)如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
18.(9分)如图所示,在△ABD和△ACE中,有下列四个论断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE.请以其中三个论断作为条件,余下一个作为结论,写出一个正确的数学命题(
)
(用序号表示),
并证明.
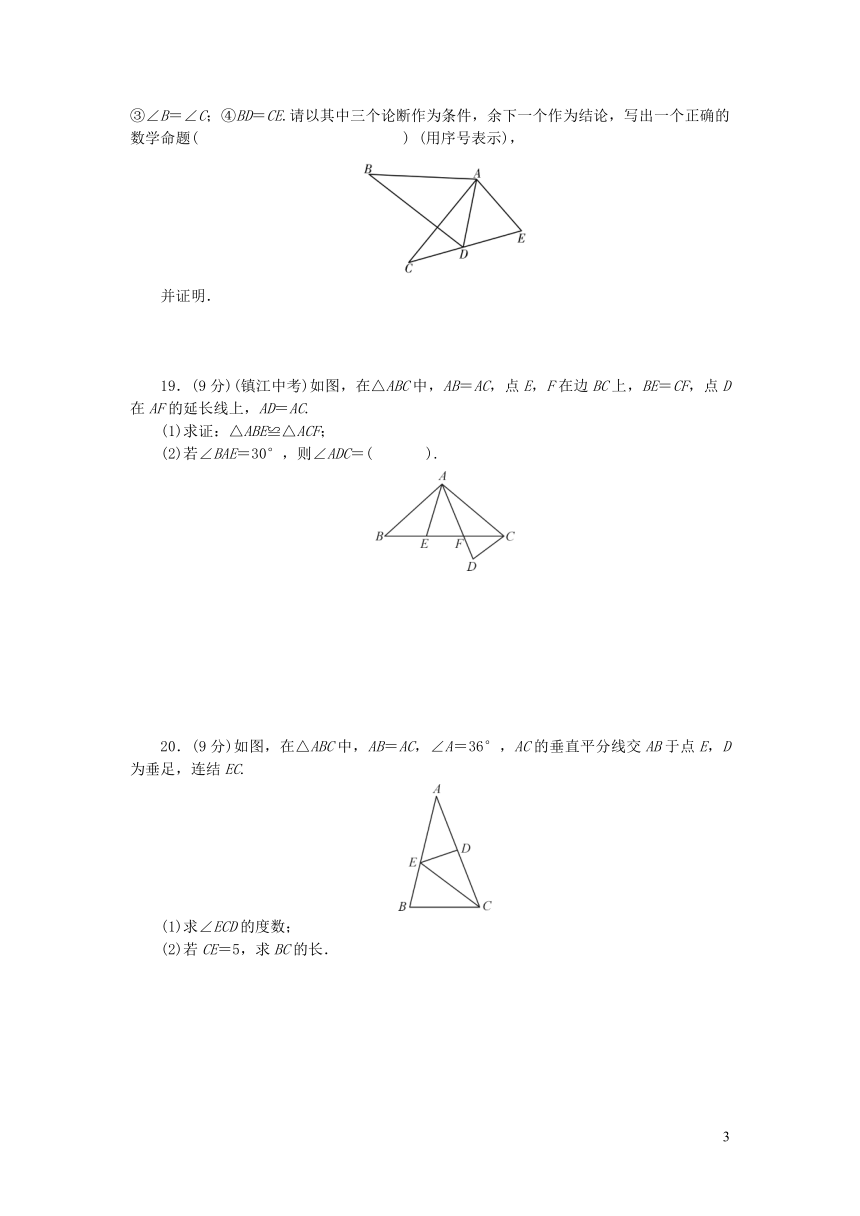
19.(9分)(镇江中考)如图,在△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC=(
).
20.(9分)如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于点E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC的长.
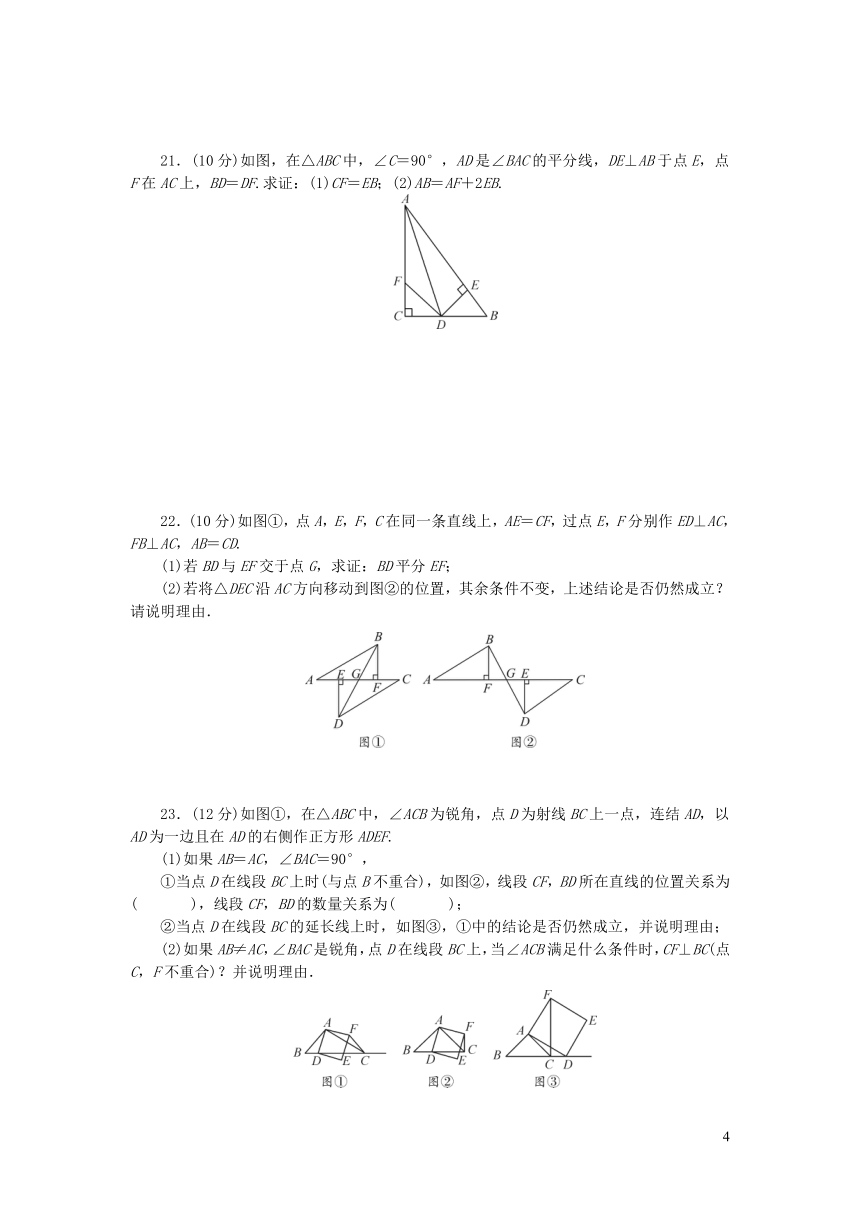
21.(10分)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,BD=DF.求证:(1)CF=EB;(2)AB=AF+2EB.
22.(10分)如图①,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作ED⊥AC,FB⊥AC,AB=CD.
(1)若BD与EF交于点G,求证:BD平分EF;
(2)若将△DEC沿AC方向移动到图②的位置,其余条件不变,上述结论是否仍然成立?请说明理由.
23.(12分)如图①,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图②,线段CF,BD所在直线的位置关系为(
),线段CF,BD的数量关系为(
);
②当点D在线段BC的延长线上时,如图③,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C,F不重合)?并说明理由.
检测内容:全等三角形(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.下列语句不是命题的是(
B
)
A.绝对值相等的两个数也相等
B.作∠AOB的平分线
C.同角的补角相等
D.长方形是轴对称图形
2.根据下列条件画三角形,不能确定唯一三角形的是(
A
)
A.已知三个角
B.已知三边
C.已知两角和夹边
D.已知两边和夹角
3.下列命题是假命题的有(
D
)
①若a2=b2,则a=b;②一个角的余角大于这个角;③若a,b是有理数,则|a+b|=|a|+|b|;④如果∠A=∠B,那么∠A与∠B是对顶角.
A.1个
B.2个
C.3个
D.4个
4.如图,已知AB=AC,AD=AE,则下列结论正确的是(
D
)
①EB=DC;②△BPE≌△CPD;③点P在∠BAC的平分线上.
A.①
B.②
C.①②
D.①②③
5.如图,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=(
B
)
A.50°
B.100°
C.120°
D.130°
6.等腰△ABC的一个外角为110°,则此等腰三角形的顶角的度数为(
C
)
A.40°
B.70°
C.40°或70°
D.以上都不对
7.(2020·陕西模拟)如图,已知△ABC的面积为8,在BC上截取BD=BA,作∠ABC的平分线交AD于点P,连接PC,则△BPC的面积为(
B
)
A.2
B.4
C.5
D.6
8.(2020·河南模拟)如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若AD=AC,∠A=80°,则∠ACB的度数为(
C
)
A.65°
B.70°
C.75°
D.80°
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是(
C
)
A.8
B.6
C.4
D.2
10.(2019·滨州)如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连结OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为(
B
)
A.4个
B.3个
C.2个
D.1个
二、填空题(每小题3分,共15分)
11.命题“如果两直线都和第三条直线互相平行,那么这两直线也互相平行”的逆命题是__如果两条直线平行,那么这两条直线都和第三条直线平行__.
12.(衢州中考)如图,在△ABC和△DEF中,点B,F,C,E在同一条直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是__AB=DE__(只需写一个,不添加辅助线).
13.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于点P,PE=3
cm,则点P到直线AB的距离是__3_cm__.
14.如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO.若∠BAC=80°,则∠BCA的度数为__60°__.
15.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为__12.5__.
三、解答题(共75分)
16.(8分)(怀化中考)两个城镇A,B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A,B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部,那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
解:如图所示
17.(8分)(武汉中考)如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
证明:∵BE=CF,∴BE+EF=CF+EF,∴BF=CE,在△ABF和△DCE中,∴△ABF≌△DCE(SAS),∴∠GEF=∠GFE,∴EG=FG
18.(9分)如图所示,在△ABD和△ACE中,有下列四个论断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE.请以其中三个论断作为条件,余下一个作为结论,写出一个正确的数学命题__由①②④得③或由①③④得②__(用序号表示),
并证明.
解:由①②④得③或由①③④得②,证明略
19.(9分)(镇江中考)如图,在△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC=____75__°.
解:(1)证明:∵AB=AC,∴∠B=∠ACF,在△ABE和△ACF中,∴△ABE≌△ACF(SAS)
20.(9分)如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于点E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC的长.
解:(1)∵DE垂直平分AC,∴AE=CE,∴∠ECD=∠A=36° (2)∵AB=AC,∠A=36°,∴∠ABC=∠ACB=72°.∵∠BEC=∠A+∠ACE=72°,∴∠B=∠BEC.∴BC=CE=5
21.(10分)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,BD=DF.求证:(1)CF=EB;(2)AB=AF+2EB.
证明:(1)∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,∴CD=ED.又∵BD=DF,∴Rt△CDF≌Rt△EDB(HL),∴CF=EB
(2)由(1)可知,CD=ED,又∵AD=AD,∴Rt△ACD≌Rt△AED(HL),∴AE=AC.又∵AC=AF+FC,AB=AE+EB,∴AB=AF+FC+EB.由(1)知EB=CF,∴AB=AF+2EB
22.(10分)如图①,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作ED⊥AC,FB⊥AC,AB=CD.
(1)若BD与EF交于点G,求证:BD平分EF;
(2)若将△DEC沿AC方向移动到图②的位置,其余条件不变,上述结论是否仍然成立?请说明理由.
解:(1)证明:∵ED⊥AC,FB⊥AC,∴∠DEG=∠BFG=90°.∵AE=CF,∴AE+EF=CF+EF,即AF=CE.在Rt△ABF和Rt△CDE中,∴Rt△ABF≌Rt△CDE(HL).∴BF=DE.又∵∠BGF=∠DGE,∴△BFG≌△DEG(AAS).∴FG=EG,即BD平分EF
(2)BD平分EF的结论仍然成立.理由:∵AE=CF,∴AE-EF=CF-EF,即AF=CE.∵ED⊥AC,FB⊥AC,∴∠AFB=∠CED=90°.在Rt△ABF和Rt△CDE中,∴Rt△ABF≌Rt△CDE(HL).∴BF=DE.易证△BFG≌△DEG(AAS),∴FG=EG,即BD平分EF
23.(12分)如图①,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图②,线段CF,BD所在直线的位置关系为____CF⊥BD__,线段CF,BD的数量关系为____CF=BD__;
②当点D在线段BC的延长线上时,如图③,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C,F不重合)?并说明理由.
解:(1)①CF⊥BD;CF=BD ②当点D在线段BC的延长线上时,①中的结论仍然成立.理由如下:由正方形ADEF得AD=AF,∠DAF=90°.∵∠BAC=90°,∴∠DAF=∠BAC,∴∠DAB=∠FAC.又∵AB=AC,∴△DAB≌△FAC,∴CF=BD,∠ACF=∠ABD.∵∠BAC=90°,AB=AC,∴△ABC是等腰直角三角形,∴∠ABC=∠ACB=45°,∴∠ACF=45°,∴∠BCF=∠ACB+∠ACF=90°,即CF⊥BD
(2)当∠ACB=45°时,CF⊥BC(如图).
理由:过点A作AG⊥AC交CB延长线于点G,则∠GAC=90°.∵∠ACB=45°,∠AGC=90°-∠ACB,∴∠AGC=90°-45°=45°,∴∠ACB=∠AGC=45°,∴△AGC是等腰直角三角形,∴AC=AG.又∵∠DAG=∠FAC(同角的余角相等),AD=AF,∴△GAD≌△CAF,∴∠ACF=∠AGC=45°,∴∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC
5
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.下列语句不是命题的是(
)
A.绝对值相等的两个数也相等
B.作∠AOB的平分线
C.同角的补角相等
D.长方形是轴对称图形
2.根据下列条件画三角形,不能确定唯一三角形的是(
)
A.已知三个角
B.已知三边
C.已知两角和夹边
D.已知两边和夹角
3.下列命题是假命题的有(
)
①若a2=b2,则a=b;②一个角的余角大于这个角;③若a,b是有理数,则|a+b|=|a|+|b|;④如果∠A=∠B,那么∠A与∠B是对顶角.
A.1个
B.2个
C.3个
D.4个
4.如图,已知AB=AC,AD=AE,则下列结论正确的是(
)
①EB=DC;②△BPE≌△CPD;③点P在∠BAC的平分线上.
A.①
B.②
C.①②
D.①②③
5.如图,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=(
)
A.50°
B.100°
C.120°
D.130°
6.等腰△ABC的一个外角为110°,则此等腰三角形的顶角的度数为(
)
A.40°
B.70°
C.40°或70°
D.以上都不对
7.(2020·陕西模拟)如图,已知△ABC的面积为8,在BC上截取BD=BA,作∠ABC的平分线交AD于点P,连接PC,则△BPC的面积为(
)
A.2
B.4
C.5
D.6
8.(2020·河南模拟)如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若AD=AC,∠A=80°,则∠ACB的度数为(
)
A.65°
B.70°
C.75°
D.80°
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是(
)
A.8
B.6
C.4
D.2
10.(2019·滨州)如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连结OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为(
)
A.4个
B.3个
C.2个
D.1个
二、填空题(每小题3分,共15分)
11.命题“如果两直线都和第三条直线互相平行,那么这两直线也互相平行”的逆命题是(
).
12.(衢州中考)如图,在△ABC和△DEF中,点B,F,C,E在同一条直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是(
)
(只需写一个,不添加辅助线).
13.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于点P,PE=3
cm,则点P到直线AB的距离是(
).
14.如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO.若∠BAC=80°,则∠BCA的度数为(
).
15.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为(
).
三、解答题(共75分)
16.(8分)(怀化中考)两个城镇A,B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A,B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部,那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
17.(8分)(武汉中考)如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
18.(9分)如图所示,在△ABD和△ACE中,有下列四个论断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE.请以其中三个论断作为条件,余下一个作为结论,写出一个正确的数学命题(
)
(用序号表示),
并证明.
19.(9分)(镇江中考)如图,在△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC=(
).
20.(9分)如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于点E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC的长.
21.(10分)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,BD=DF.求证:(1)CF=EB;(2)AB=AF+2EB.
22.(10分)如图①,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作ED⊥AC,FB⊥AC,AB=CD.
(1)若BD与EF交于点G,求证:BD平分EF;
(2)若将△DEC沿AC方向移动到图②的位置,其余条件不变,上述结论是否仍然成立?请说明理由.
23.(12分)如图①,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图②,线段CF,BD所在直线的位置关系为(
),线段CF,BD的数量关系为(
);
②当点D在线段BC的延长线上时,如图③,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C,F不重合)?并说明理由.
检测内容:全等三角形(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.下列语句不是命题的是(
B
)
A.绝对值相等的两个数也相等
B.作∠AOB的平分线
C.同角的补角相等
D.长方形是轴对称图形
2.根据下列条件画三角形,不能确定唯一三角形的是(
A
)
A.已知三个角
B.已知三边
C.已知两角和夹边
D.已知两边和夹角
3.下列命题是假命题的有(
D
)
①若a2=b2,则a=b;②一个角的余角大于这个角;③若a,b是有理数,则|a+b|=|a|+|b|;④如果∠A=∠B,那么∠A与∠B是对顶角.
A.1个
B.2个
C.3个
D.4个
4.如图,已知AB=AC,AD=AE,则下列结论正确的是(
D
)
①EB=DC;②△BPE≌△CPD;③点P在∠BAC的平分线上.
A.①
B.②
C.①②
D.①②③
5.如图,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=(
B
)
A.50°
B.100°
C.120°
D.130°
6.等腰△ABC的一个外角为110°,则此等腰三角形的顶角的度数为(
C
)
A.40°
B.70°
C.40°或70°
D.以上都不对
7.(2020·陕西模拟)如图,已知△ABC的面积为8,在BC上截取BD=BA,作∠ABC的平分线交AD于点P,连接PC,则△BPC的面积为(
B
)
A.2
B.4
C.5
D.6
8.(2020·河南模拟)如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若AD=AC,∠A=80°,则∠ACB的度数为(
C
)
A.65°
B.70°
C.75°
D.80°
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是(
C
)
A.8
B.6
C.4
D.2
10.(2019·滨州)如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连结OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为(
B
)
A.4个
B.3个
C.2个
D.1个
二、填空题(每小题3分,共15分)
11.命题“如果两直线都和第三条直线互相平行,那么这两直线也互相平行”的逆命题是__如果两条直线平行,那么这两条直线都和第三条直线平行__.
12.(衢州中考)如图,在△ABC和△DEF中,点B,F,C,E在同一条直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是__AB=DE__(只需写一个,不添加辅助线).
13.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于点P,PE=3
cm,则点P到直线AB的距离是__3_cm__.
14.如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO.若∠BAC=80°,则∠BCA的度数为__60°__.
15.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为__12.5__.
三、解答题(共75分)
16.(8分)(怀化中考)两个城镇A,B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A,B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部,那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
解:如图所示
17.(8分)(武汉中考)如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
证明:∵BE=CF,∴BE+EF=CF+EF,∴BF=CE,在△ABF和△DCE中,∴△ABF≌△DCE(SAS),∴∠GEF=∠GFE,∴EG=FG
18.(9分)如图所示,在△ABD和△ACE中,有下列四个论断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE.请以其中三个论断作为条件,余下一个作为结论,写出一个正确的数学命题__由①②④得③或由①③④得②__(用序号表示),
并证明.
解:由①②④得③或由①③④得②,证明略
19.(9分)(镇江中考)如图,在△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC=____75__°.
解:(1)证明:∵AB=AC,∴∠B=∠ACF,在△ABE和△ACF中,∴△ABE≌△ACF(SAS)
20.(9分)如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于点E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC的长.
解:(1)∵DE垂直平分AC,∴AE=CE,∴∠ECD=∠A=36° (2)∵AB=AC,∠A=36°,∴∠ABC=∠ACB=72°.∵∠BEC=∠A+∠ACE=72°,∴∠B=∠BEC.∴BC=CE=5
21.(10分)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,BD=DF.求证:(1)CF=EB;(2)AB=AF+2EB.
证明:(1)∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,∴CD=ED.又∵BD=DF,∴Rt△CDF≌Rt△EDB(HL),∴CF=EB
(2)由(1)可知,CD=ED,又∵AD=AD,∴Rt△ACD≌Rt△AED(HL),∴AE=AC.又∵AC=AF+FC,AB=AE+EB,∴AB=AF+FC+EB.由(1)知EB=CF,∴AB=AF+2EB
22.(10分)如图①,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作ED⊥AC,FB⊥AC,AB=CD.
(1)若BD与EF交于点G,求证:BD平分EF;
(2)若将△DEC沿AC方向移动到图②的位置,其余条件不变,上述结论是否仍然成立?请说明理由.
解:(1)证明:∵ED⊥AC,FB⊥AC,∴∠DEG=∠BFG=90°.∵AE=CF,∴AE+EF=CF+EF,即AF=CE.在Rt△ABF和Rt△CDE中,∴Rt△ABF≌Rt△CDE(HL).∴BF=DE.又∵∠BGF=∠DGE,∴△BFG≌△DEG(AAS).∴FG=EG,即BD平分EF
(2)BD平分EF的结论仍然成立.理由:∵AE=CF,∴AE-EF=CF-EF,即AF=CE.∵ED⊥AC,FB⊥AC,∴∠AFB=∠CED=90°.在Rt△ABF和Rt△CDE中,∴Rt△ABF≌Rt△CDE(HL).∴BF=DE.易证△BFG≌△DEG(AAS),∴FG=EG,即BD平分EF
23.(12分)如图①,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图②,线段CF,BD所在直线的位置关系为____CF⊥BD__,线段CF,BD的数量关系为____CF=BD__;
②当点D在线段BC的延长线上时,如图③,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C,F不重合)?并说明理由.
解:(1)①CF⊥BD;CF=BD ②当点D在线段BC的延长线上时,①中的结论仍然成立.理由如下:由正方形ADEF得AD=AF,∠DAF=90°.∵∠BAC=90°,∴∠DAF=∠BAC,∴∠DAB=∠FAC.又∵AB=AC,∴△DAB≌△FAC,∴CF=BD,∠ACF=∠ABD.∵∠BAC=90°,AB=AC,∴△ABC是等腰直角三角形,∴∠ABC=∠ACB=45°,∴∠ACF=45°,∴∠BCF=∠ACB+∠ACF=90°,即CF⊥BD
(2)当∠ACB=45°时,CF⊥BC(如图).
理由:过点A作AG⊥AC交CB延长线于点G,则∠GAC=90°.∵∠ACB=45°,∠AGC=90°-∠ACB,∴∠AGC=90°-45°=45°,∴∠ACB=∠AGC=45°,∴△AGC是等腰直角三角形,∴AC=AG.又∵∠DAG=∠FAC(同角的余角相等),AD=AF,∴△GAD≌△CAF,∴∠ACF=∠AGC=45°,∴∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC
5
