华东师大版八年级数学上册 第14章勾股定理测试题(word版,含答案)
文档属性
| 名称 | 华东师大版八年级数学上册 第14章勾股定理测试题(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 00:00:00 | ||
图片预览


文档简介
检测内容:勾股定理
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.在Rt△ABC中,∠B=90°,BC=1,AC=2,则AB的长是(
)
A.1 B. C.2 D.
2.以下列各组数为边长,不能构成直角三角形的是(
)
A.3,4,5
B.1,1,
C.8,12,13
D.,,
3.若一个直角三角形的两边长分别为12和5,则第三边长为(
)
A.13
B.13或
C.13或15
D.15
4.如图,如果半圆的直径恰为直角三角形的一条直角边,那么这个半圆的面积为(
)
A.4π
cm2
B.6π
cm2
C.12π
cm2
D.24π
cm2
5.等腰三角形底边长为10,腰长为13,则此三角形的面积为(
)
A.40
B.50
C.60
D.70
6.直角三角形中,斜边长为2
cm,周长为(2+)
cm,则它的面积为(
)
A.1.5
cm2
B.2
cm2
C.3
cm2
D.6
cm2
7.如图,在Rt△ABC中,∠B=90°,AB=3
cm,AC=5
cm,将△ABC折叠,使点C与A重合,得折痕为DE,则△ABE的周长为(
)
A.5
cm
B.6
cm
C.7
cm
D.8
cm
8.用四个全等的直角三角形镶嵌而成的正方形如图所示,已知大正方形的面积为49,小正方形的面积为4,若x,y表示直角三角形的两直角边长(x>y),给出下列四个结论:①x2+y2=49;②x-y=2;③2xy=45;④x+y=9.其中正确的结论是(
)
A.①②③
B.①②③④
C.①③
D.②④
9.如图,某学校A与直线公路l的距离为3
000
m,与该公路上某车站D的距离为5
000
m,现要在公路边建一个小商店C,使之与学校A及车站D的距离相等,那么该商店与车站之间的距离是(
)
A.1
800
m
B.2
000
m
C.3
000
m
D.3
125
m
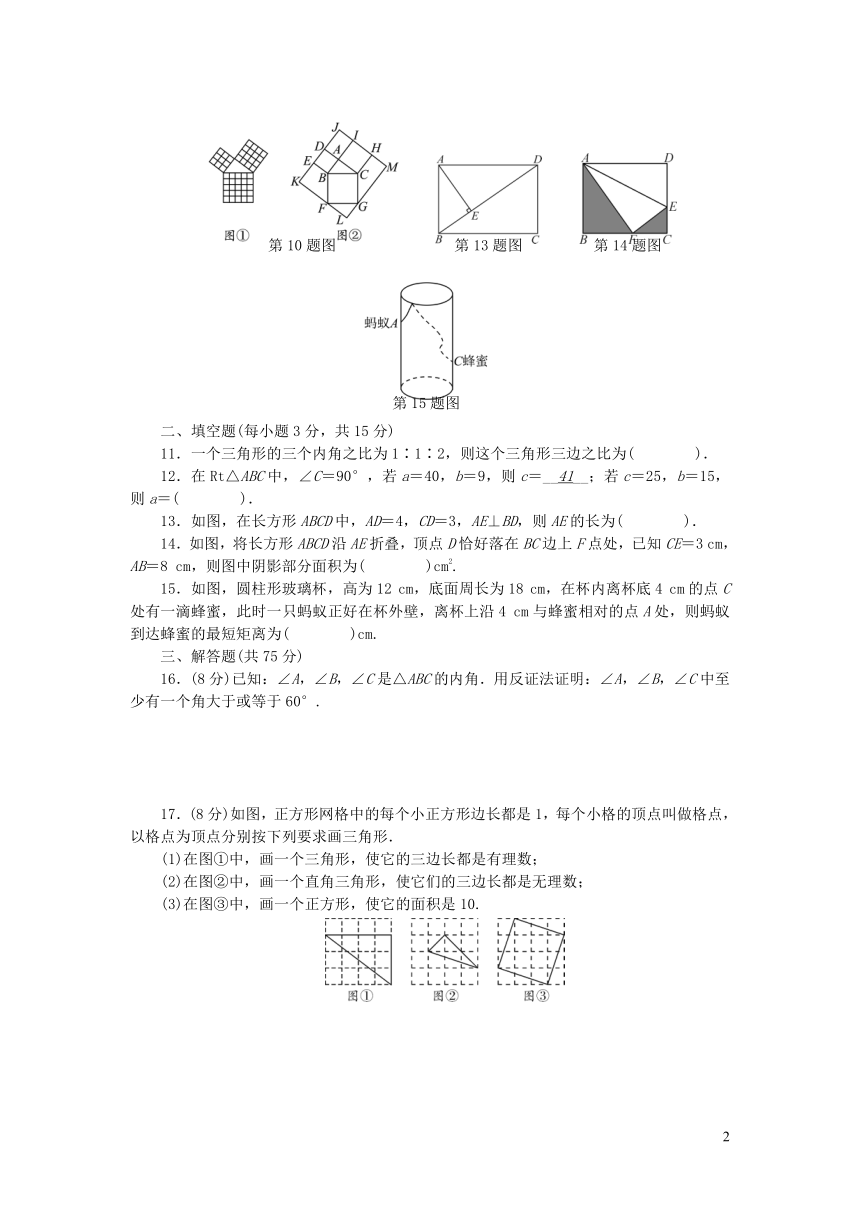
10.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图①是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图②是由图①放入长方形内得到的,∠BAC=90°,AB=3,AC=4,若D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为(
)
A.90
B.100
C.110
D.121
二、填空题(每小题3分,共15分)
11.一个三角形的三个内角之比为1∶1∶2,则这个三角形三边之比为(
).
12.在Rt△ABC中,∠C=90°,若a=40,b=9,则c=__41__;若c=25,b=15,则a=(
).
13.如图,在长方形ABCD中,AD=4,CD=3,AE⊥BD,则AE的长为(
).
14.如图,将长方形ABCD沿AE折叠,顶点D恰好落在BC边上F点处,已知CE=3
cm,AB=8
cm,则图中阴影部分面积为(
)cm2.
15.如图,圆柱形玻璃杯,高为12
cm,底面周长为18
cm,在杯内离杯底4
cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4
cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短矩离为(
)cm.
三、解答题(共75分)
16.(8分)已知:∠A,∠B,∠C是△ABC的内角.用反证法证明:∠A,∠B,∠C中至少有一个角大于或等于60°.
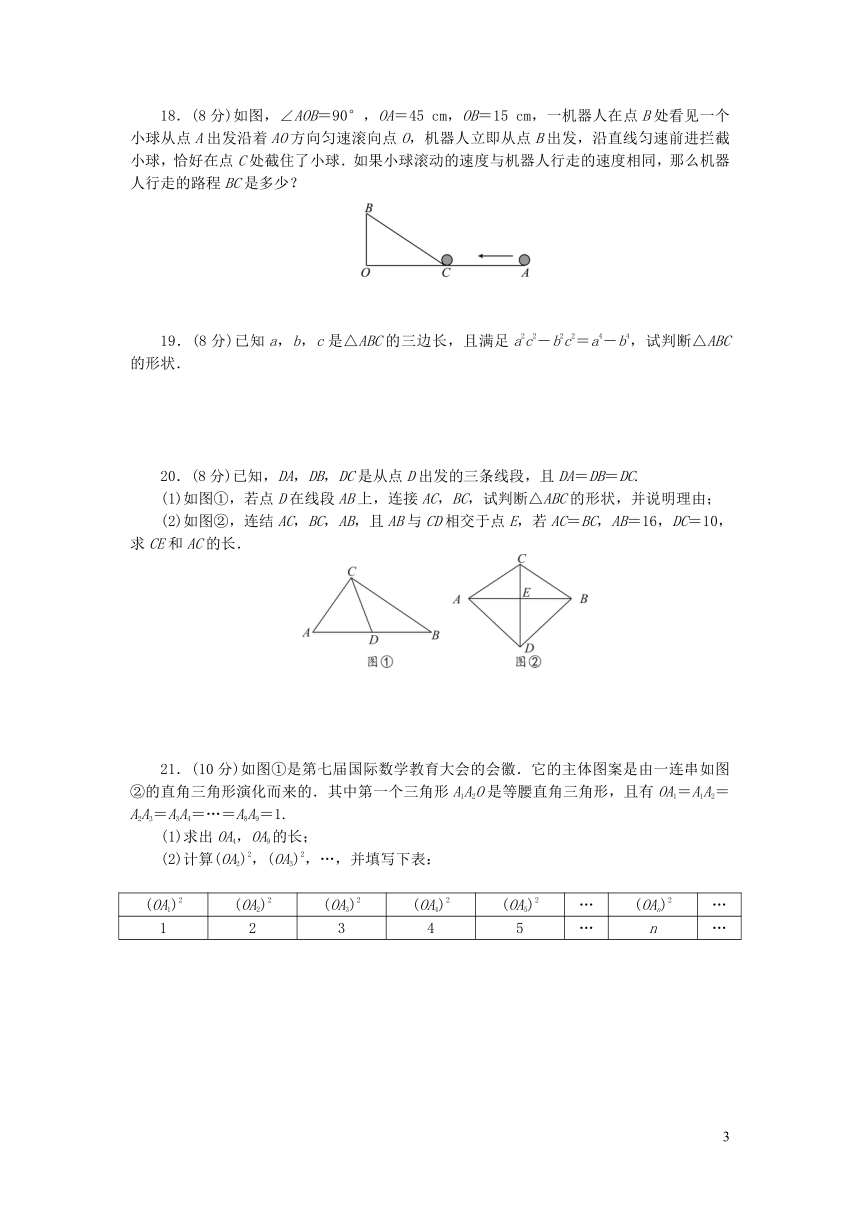
17.(8分)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图①中,画一个三角形,使它的三边长都是有理数;
(2)在图②中,画一个直角三角形,使它们的三边长都是无理数;
(3)在图③中,画一个正方形,使它的面积是10.
18.(8分)如图,∠AOB=90°,OA=45
cm,OB=15
cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相同,那么机器人行走的路程BC是多少?
19.(8分)已知a,b,c是△ABC的三边长,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
20.(8分)已知,DA,DB,DC是从点D出发的三条线段,且DA=DB=DC.
(1)如图①,若点D在线段AB上,连接AC,BC,试判断△ABC的形状,并说明理由;
(2)如图②,连结AC,BC,AB,且AB与CD相交于点E,若AC=BC,AB=16,DC=10,求CE和AC的长.
21.(10分)如图①是第七届国际数学教育大会的会徽.它的主体图案是由一连串如图②的直角三角形演化而来的.其中第一个三角形A1A2O是等腰直角三角形,且有OA1=A1A2=A2A3=A3A4=…=A8A9=1.
(1)求出OA4,OA9的长;
(2)计算(OA2)2,(OA3)2,…,并填写下表:
(OA1)2
(OA2)2
(OA3)2
(OA4)2
(OA5)2
…
(OAn)2
…
1
2
3
4
5
…
n
…
22.(12分)在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6,8,9时,△ABC为(
)三角形;当△ABC三边分别为6,8,11时,△ABC为(
)三角形;
(2)猜想,当a2+b2(
)c2时,△ABC为锐角三角形;当a2+b2_(
)c2时,△ABC为钝角三角形;
(3)判断当a=2,b=4时△ABC的形状,并求出对应的c的取值范围.
23.(13分)阅读下面材料:
实际问题:如图①,一圆柱的底面半径为5厘米,BC是底面直径,高AB为5厘米,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.
解决方案:
路线1:侧面展开图中的线段AC,如图②所示,
设路线1的长度为l1:则l12=AC2=AB2+BC2=52+(5π)2=25+25π2;
路线2:高线AB+底面直径BC,如图①所示.
设路线2的长度为l2:则l22=(AB+dBC)2=(5+10)2=225.
为比较l1,l2的大小,我们采用“作差法”:
∵l12-l22=25(π2-8)>0,∴l12>l22,∴l1>l2,
小明认为应选择路线2较短.
(1)问题类比:小亮对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1厘米,高AB为5厘米.”请你用上述方法帮小亮比较出l1与l2的大小;
(2)问题拓展:请你帮他们继续研究:在一般情况下,当圆柱的底面半径为r厘米时,高为h厘米,蚂蚁从A点出发沿圆柱表面爬行到点C,当满足什么条件时,选择路线2最短?请说明理由;
(3)问题解决:如图③为2个相同的圆柱紧密排列在一起,高为5厘米,当蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.(注:按上面小明所设计的两条路线方式)
检测内容:勾股定理(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.在Rt△ABC中,∠B=90°,BC=1,AC=2,则AB的长是(
B
)
A.1 B. C.2 D.
2.以下列各组数为边长,不能构成直角三角形的是(
C
)
A.3,4,5
B.1,1,
C.8,12,13
D.,,
3.若一个直角三角形的两边长分别为12和5,则第三边长为(
B
)
A.13
B.13或
C.13或15
D.15
4.如图,如果半圆的直径恰为直角三角形的一条直角边,那么这个半圆的面积为(
B
)
A.4π
cm2
B.6π
cm2
C.12π
cm2
D.24π
cm2
5.等腰三角形底边长为10,腰长为13,则此三角形的面积为(
C
)
A.40
B.50
C.60
D.70
6.直角三角形中,斜边长为2
cm,周长为(2+)
cm,则它的面积为(
A
)
A.1.5
cm2
B.2
cm2
C.3
cm2
D.6
cm2
7.如图,在Rt△ABC中,∠B=90°,AB=3
cm,AC=5
cm,将△ABC折叠,使点C与A重合,得折痕为DE,则△ABE的周长为(
C
)
A.5
cm
B.6
cm
C.7
cm
D.8
cm
8.用四个全等的直角三角形镶嵌而成的正方形如图所示,已知大正方形的面积为49,小正方形的面积为4,若x,y表示直角三角形的两直角边长(x>y),给出下列四个结论:①x2+y2=49;②x-y=2;③2xy=45;④x+y=9.其中正确的结论是(
A
)
A.①②③
B.①②③④
C.①③
D.②④
9.如图,某学校A与直线公路l的距离为3
000
m,与该公路上某车站D的距离为5
000
m,现要在公路边建一个小商店C,使之与学校A及车站D的距离相等,那么该商店与车站之间的距离是(
D
)
A.1
800
m
B.2
000
m
C.3
000
m
D.3
125
m
10.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图①是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图②是由图①放入长方形内得到的,∠BAC=90°,AB=3,AC=4,若D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为(
C
)
A.90
B.100
C.110
D.121
二、填空题(每小题3分,共15分)
11.一个三角形的三个内角之比为1∶1∶2,则这个三角形三边之比为__1∶1∶__.
12.在Rt△ABC中,∠C=90°,若a=40,b=9,则c=__41__;若c=25,b=15,则a=__20__.
13.如图,在长方形ABCD中,AD=4,CD=3,AE⊥BD,则AE的长为____.
14.如图,将长方形ABCD沿AE折叠,顶点D恰好落在BC边上F点处,已知CE=3
cm,AB=8
cm,则图中阴影部分面积为__30__cm2.
15.如图,圆柱形玻璃杯,高为12
cm,底面周长为18
cm,在杯内离杯底4
cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4
cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短矩离为__15__cm.
三、解答题(共75分)
16.(8分)已知:∠A,∠B,∠C是△ABC的内角.用反证法证明:∠A,∠B,∠C中至少有一个角大于或等于60°.
证明:假设∠A,∠B,∠C中没有一个角大于或等于60°,即∠A<60°,∠B<60°,∠C<60°,则∠A+∠B+∠C<180°.这与“三角形的内角和等于180°”矛盾,所以假设不成立.因此,∠A,∠B,∠C中至少有一个角大于或等于60°
17.(8分)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图①中,画一个三角形,使它的三边长都是有理数;
(2)在图②中,画一个直角三角形,使它们的三边长都是无理数;
(3)在图③中,画一个正方形,使它的面积是10.
解:(1)三边分别为3,4,5(如图①)
(2)三边分别为,,(如图②)
(3)画一个边长为的正方形(如图③)
18.(8分)如图,∠AOB=90°,OA=45
cm,OB=15
cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相同,那么机器人行走的路程BC是多少?
解:BC=25
cm
19.(8分)已知a,b,c是△ABC的三边长,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:由已知得a4-b4-a2c2+b2c2=0,(a2+b2)(a2-b2)-c2(a2-b2)=0,(a2-b2)(a2+b2-c2)=0,∴a2=b2或a2+b2=c2,即a=b(a>0,b>0)或a2+b2=c2,∴△ABC是等腰三角形或△ABC是直角三角形
20.(8分)已知,DA,DB,DC是从点D出发的三条线段,且DA=DB=DC.
(1)如图①,若点D在线段AB上,连接AC,BC,试判断△ABC的形状,并说明理由;
(2)如图②,连结AC,BC,AB,且AB与CD相交于点E,若AC=BC,AB=16,DC=10,求CE和AC的长.
解:(1)△ABC是直角三角形,理由:∵DA=DB=DC,∴∠A=∠ACD,∠B=∠BCD,∵∠A+∠ACD+∠B+∠BCD=180°,∴∠ACD+∠BCD=90°,∴∠ACB=90°,∴△ABC是直角三角形
(2)∵DA=DB,∴点D在线段AB的垂直平分线上,∵AC=BC,∴点C在线段AB的垂直平分线上,∴CD垂直平分AB,∴∠AEC=∠AED=90°,∵AB=16,DC=10,∴AE=8,AD=CD=10,∴DE==6,∴CE=CD-DE=4,∴AC===4
21.(10分)如图①是第七届国际数学教育大会的会徽.它的主体图案是由一连串如图②的直角三角形演化而来的.其中第一个三角形A1A2O是等腰直角三角形,且有OA1=A1A2=A2A3=A3A4=…=A8A9=1.
(1)求出OA4,OA9的长;
(2)计算(OA2)2,(OA3)2,…,并填写下表:
(OA1)2
(OA2)2
(OA3)2
(OA4)2
(OA5)2
…
(OAn)2
…
1
2
3
4
5
…
n
…
解:(1)(OA4)2=(A3A4)2+(OA3)2=(A3A4)2+(A2A3)2+(OA2)2=(A3A4)2+(A2A3)2+(A1A2)2+(OA1)2=1+1+1+1=4,则OA4=2,同理得OA9=3 (2)表格从左到右依次填3,4,5,n
22.(12分)在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6,8,9时,△ABC为__锐角__三角形;当△ABC三边分别为6,8,11时,△ABC为__钝角__三角形;
(2)猜想,当a2+b2__>__c2时,△ABC为锐角三角形;当a2+b2__<__c2时,△ABC为钝角三角形;
(3)判断当a=2,b=4时△ABC的形状,并求出对应的c的取值范围.
解:(3)∵c为最长边,2+4=6,∴4≤c<6,a2+b2=22+42=20,①a2+b2>c2,即c2<20,0<c<2,∴当4≤c<2时,这个三角形是锐角三角形;②a2+b2=c2,即c2=20,c=2,∴当c=2时,这个三角形是直角三角形;③a2+b2<c2,即c2>20,c>2,∴当2<c<6时,这个三角形是钝角三角形
23.(13分)阅读下面材料:
实际问题:如图①,一圆柱的底面半径为5厘米,BC是底面直径,高AB为5厘米,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.
解决方案:
路线1:侧面展开图中的线段AC,如图②所示,
设路线1的长度为l1:则l12=AC2=AB2+BC2=52+(5π)2=25+25π2;
路线2:高线AB+底面直径BC,如图①所示.
设路线2的长度为l2:则l22=(AB+dBC)2=(5+10)2=225.
为比较l1,l2的大小,我们采用“作差法”:
∵l12-l22=25(π2-8)>0,∴l12>l22,∴l1>l2,
小明认为应选择路线2较短.
(1)问题类比:小亮对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1厘米,高AB为5厘米.”请你用上述方法帮小亮比较出l1与l2的大小;
(2)问题拓展:请你帮他们继续研究:在一般情况下,当圆柱的底面半径为r厘米时,高为h厘米,蚂蚁从A点出发沿圆柱表面爬行到点C,当满足什么条件时,选择路线2最短?请说明理由;
(3)问题解决:如图③为2个相同的圆柱紧密排列在一起,高为5厘米,当蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.(注:按上面小明所设计的两条路线方式)
解:(1)如图②.∵圆柱的底面半径为1厘米,高AB为5厘米,
∴路线1:l12=AC2=AB2+BC2=25+π2;
路线2:l2=AB+dBC=5+2=7,l22=(AB+dBC)2=49.
∵l12-l22=25+π2-49=π2-24<0,∴l12(2)如图②.∵圆柱的底面半径为r厘米,高为h厘米,
∴路线1:l12=AC2=AB2+BC2=h2+(πr)2=h2+π2r2,路线2:l22=(AB+dBC)2=(h+2r)2,
∴l12-l22=h2+(πr)2-(h+2r)2=r(π2r-4r-4h)=r[(π2-4)r-4h];
∵r恒大于0,∴当(π2-4)r-4h>0,即>时,l12>l22,即此时选择的路2最短
(3)如图③,圆柱的高为5厘米.l12=AC2=AB2+BC2=25+(2πr)2,
l22=(AB+dBC)2=(5+4r)2,由题意,得25+(2πr)2=(5+4r)2,解得r=.
即当圆柱的底面半径r为厘米时,蚂蚁从点A出发沿圆柱表面爬行到C点的两条线段相等
5
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.在Rt△ABC中,∠B=90°,BC=1,AC=2,则AB的长是(
)
A.1 B. C.2 D.
2.以下列各组数为边长,不能构成直角三角形的是(
)
A.3,4,5
B.1,1,
C.8,12,13
D.,,
3.若一个直角三角形的两边长分别为12和5,则第三边长为(
)
A.13
B.13或
C.13或15
D.15
4.如图,如果半圆的直径恰为直角三角形的一条直角边,那么这个半圆的面积为(
)
A.4π
cm2
B.6π
cm2
C.12π
cm2
D.24π
cm2
5.等腰三角形底边长为10,腰长为13,则此三角形的面积为(
)
A.40
B.50
C.60
D.70
6.直角三角形中,斜边长为2
cm,周长为(2+)
cm,则它的面积为(
)
A.1.5
cm2
B.2
cm2
C.3
cm2
D.6
cm2
7.如图,在Rt△ABC中,∠B=90°,AB=3
cm,AC=5
cm,将△ABC折叠,使点C与A重合,得折痕为DE,则△ABE的周长为(
)
A.5
cm
B.6
cm
C.7
cm
D.8
cm
8.用四个全等的直角三角形镶嵌而成的正方形如图所示,已知大正方形的面积为49,小正方形的面积为4,若x,y表示直角三角形的两直角边长(x>y),给出下列四个结论:①x2+y2=49;②x-y=2;③2xy=45;④x+y=9.其中正确的结论是(
)
A.①②③
B.①②③④
C.①③
D.②④
9.如图,某学校A与直线公路l的距离为3
000
m,与该公路上某车站D的距离为5
000
m,现要在公路边建一个小商店C,使之与学校A及车站D的距离相等,那么该商店与车站之间的距离是(
)
A.1
800
m
B.2
000
m
C.3
000
m
D.3
125
m
10.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图①是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图②是由图①放入长方形内得到的,∠BAC=90°,AB=3,AC=4,若D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为(
)
A.90
B.100
C.110
D.121
二、填空题(每小题3分,共15分)
11.一个三角形的三个内角之比为1∶1∶2,则这个三角形三边之比为(
).
12.在Rt△ABC中,∠C=90°,若a=40,b=9,则c=__41__;若c=25,b=15,则a=(
).
13.如图,在长方形ABCD中,AD=4,CD=3,AE⊥BD,则AE的长为(
).
14.如图,将长方形ABCD沿AE折叠,顶点D恰好落在BC边上F点处,已知CE=3
cm,AB=8
cm,则图中阴影部分面积为(
)cm2.
15.如图,圆柱形玻璃杯,高为12
cm,底面周长为18
cm,在杯内离杯底4
cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4
cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短矩离为(
)cm.
三、解答题(共75分)
16.(8分)已知:∠A,∠B,∠C是△ABC的内角.用反证法证明:∠A,∠B,∠C中至少有一个角大于或等于60°.
17.(8分)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图①中,画一个三角形,使它的三边长都是有理数;
(2)在图②中,画一个直角三角形,使它们的三边长都是无理数;
(3)在图③中,画一个正方形,使它的面积是10.
18.(8分)如图,∠AOB=90°,OA=45
cm,OB=15
cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相同,那么机器人行走的路程BC是多少?
19.(8分)已知a,b,c是△ABC的三边长,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
20.(8分)已知,DA,DB,DC是从点D出发的三条线段,且DA=DB=DC.
(1)如图①,若点D在线段AB上,连接AC,BC,试判断△ABC的形状,并说明理由;
(2)如图②,连结AC,BC,AB,且AB与CD相交于点E,若AC=BC,AB=16,DC=10,求CE和AC的长.
21.(10分)如图①是第七届国际数学教育大会的会徽.它的主体图案是由一连串如图②的直角三角形演化而来的.其中第一个三角形A1A2O是等腰直角三角形,且有OA1=A1A2=A2A3=A3A4=…=A8A9=1.
(1)求出OA4,OA9的长;
(2)计算(OA2)2,(OA3)2,…,并填写下表:
(OA1)2
(OA2)2
(OA3)2
(OA4)2
(OA5)2
…
(OAn)2
…
1
2
3
4
5
…
n
…
22.(12分)在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6,8,9时,△ABC为(
)三角形;当△ABC三边分别为6,8,11时,△ABC为(
)三角形;
(2)猜想,当a2+b2(
)c2时,△ABC为锐角三角形;当a2+b2_(
)c2时,△ABC为钝角三角形;
(3)判断当a=2,b=4时△ABC的形状,并求出对应的c的取值范围.
23.(13分)阅读下面材料:
实际问题:如图①,一圆柱的底面半径为5厘米,BC是底面直径,高AB为5厘米,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.
解决方案:
路线1:侧面展开图中的线段AC,如图②所示,
设路线1的长度为l1:则l12=AC2=AB2+BC2=52+(5π)2=25+25π2;
路线2:高线AB+底面直径BC,如图①所示.
设路线2的长度为l2:则l22=(AB+dBC)2=(5+10)2=225.
为比较l1,l2的大小,我们采用“作差法”:
∵l12-l22=25(π2-8)>0,∴l12>l22,∴l1>l2,
小明认为应选择路线2较短.
(1)问题类比:小亮对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1厘米,高AB为5厘米.”请你用上述方法帮小亮比较出l1与l2的大小;
(2)问题拓展:请你帮他们继续研究:在一般情况下,当圆柱的底面半径为r厘米时,高为h厘米,蚂蚁从A点出发沿圆柱表面爬行到点C,当满足什么条件时,选择路线2最短?请说明理由;
(3)问题解决:如图③为2个相同的圆柱紧密排列在一起,高为5厘米,当蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.(注:按上面小明所设计的两条路线方式)
检测内容:勾股定理(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.在Rt△ABC中,∠B=90°,BC=1,AC=2,则AB的长是(
B
)
A.1 B. C.2 D.
2.以下列各组数为边长,不能构成直角三角形的是(
C
)
A.3,4,5
B.1,1,
C.8,12,13
D.,,
3.若一个直角三角形的两边长分别为12和5,则第三边长为(
B
)
A.13
B.13或
C.13或15
D.15
4.如图,如果半圆的直径恰为直角三角形的一条直角边,那么这个半圆的面积为(
B
)
A.4π
cm2
B.6π
cm2
C.12π
cm2
D.24π
cm2
5.等腰三角形底边长为10,腰长为13,则此三角形的面积为(
C
)
A.40
B.50
C.60
D.70
6.直角三角形中,斜边长为2
cm,周长为(2+)
cm,则它的面积为(
A
)
A.1.5
cm2
B.2
cm2
C.3
cm2
D.6
cm2
7.如图,在Rt△ABC中,∠B=90°,AB=3
cm,AC=5
cm,将△ABC折叠,使点C与A重合,得折痕为DE,则△ABE的周长为(
C
)
A.5
cm
B.6
cm
C.7
cm
D.8
cm
8.用四个全等的直角三角形镶嵌而成的正方形如图所示,已知大正方形的面积为49,小正方形的面积为4,若x,y表示直角三角形的两直角边长(x>y),给出下列四个结论:①x2+y2=49;②x-y=2;③2xy=45;④x+y=9.其中正确的结论是(
A
)
A.①②③
B.①②③④
C.①③
D.②④
9.如图,某学校A与直线公路l的距离为3
000
m,与该公路上某车站D的距离为5
000
m,现要在公路边建一个小商店C,使之与学校A及车站D的距离相等,那么该商店与车站之间的距离是(
D
)
A.1
800
m
B.2
000
m
C.3
000
m
D.3
125
m
10.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图①是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图②是由图①放入长方形内得到的,∠BAC=90°,AB=3,AC=4,若D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为(
C
)
A.90
B.100
C.110
D.121
二、填空题(每小题3分,共15分)
11.一个三角形的三个内角之比为1∶1∶2,则这个三角形三边之比为__1∶1∶__.
12.在Rt△ABC中,∠C=90°,若a=40,b=9,则c=__41__;若c=25,b=15,则a=__20__.
13.如图,在长方形ABCD中,AD=4,CD=3,AE⊥BD,则AE的长为____.
14.如图,将长方形ABCD沿AE折叠,顶点D恰好落在BC边上F点处,已知CE=3
cm,AB=8
cm,则图中阴影部分面积为__30__cm2.
15.如图,圆柱形玻璃杯,高为12
cm,底面周长为18
cm,在杯内离杯底4
cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4
cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短矩离为__15__cm.
三、解答题(共75分)
16.(8分)已知:∠A,∠B,∠C是△ABC的内角.用反证法证明:∠A,∠B,∠C中至少有一个角大于或等于60°.
证明:假设∠A,∠B,∠C中没有一个角大于或等于60°,即∠A<60°,∠B<60°,∠C<60°,则∠A+∠B+∠C<180°.这与“三角形的内角和等于180°”矛盾,所以假设不成立.因此,∠A,∠B,∠C中至少有一个角大于或等于60°
17.(8分)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图①中,画一个三角形,使它的三边长都是有理数;
(2)在图②中,画一个直角三角形,使它们的三边长都是无理数;
(3)在图③中,画一个正方形,使它的面积是10.
解:(1)三边分别为3,4,5(如图①)
(2)三边分别为,,(如图②)
(3)画一个边长为的正方形(如图③)
18.(8分)如图,∠AOB=90°,OA=45
cm,OB=15
cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相同,那么机器人行走的路程BC是多少?
解:BC=25
cm
19.(8分)已知a,b,c是△ABC的三边长,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:由已知得a4-b4-a2c2+b2c2=0,(a2+b2)(a2-b2)-c2(a2-b2)=0,(a2-b2)(a2+b2-c2)=0,∴a2=b2或a2+b2=c2,即a=b(a>0,b>0)或a2+b2=c2,∴△ABC是等腰三角形或△ABC是直角三角形
20.(8分)已知,DA,DB,DC是从点D出发的三条线段,且DA=DB=DC.
(1)如图①,若点D在线段AB上,连接AC,BC,试判断△ABC的形状,并说明理由;
(2)如图②,连结AC,BC,AB,且AB与CD相交于点E,若AC=BC,AB=16,DC=10,求CE和AC的长.
解:(1)△ABC是直角三角形,理由:∵DA=DB=DC,∴∠A=∠ACD,∠B=∠BCD,∵∠A+∠ACD+∠B+∠BCD=180°,∴∠ACD+∠BCD=90°,∴∠ACB=90°,∴△ABC是直角三角形
(2)∵DA=DB,∴点D在线段AB的垂直平分线上,∵AC=BC,∴点C在线段AB的垂直平分线上,∴CD垂直平分AB,∴∠AEC=∠AED=90°,∵AB=16,DC=10,∴AE=8,AD=CD=10,∴DE==6,∴CE=CD-DE=4,∴AC===4
21.(10分)如图①是第七届国际数学教育大会的会徽.它的主体图案是由一连串如图②的直角三角形演化而来的.其中第一个三角形A1A2O是等腰直角三角形,且有OA1=A1A2=A2A3=A3A4=…=A8A9=1.
(1)求出OA4,OA9的长;
(2)计算(OA2)2,(OA3)2,…,并填写下表:
(OA1)2
(OA2)2
(OA3)2
(OA4)2
(OA5)2
…
(OAn)2
…
1
2
3
4
5
…
n
…
解:(1)(OA4)2=(A3A4)2+(OA3)2=(A3A4)2+(A2A3)2+(OA2)2=(A3A4)2+(A2A3)2+(A1A2)2+(OA1)2=1+1+1+1=4,则OA4=2,同理得OA9=3 (2)表格从左到右依次填3,4,5,n
22.(12分)在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6,8,9时,△ABC为__锐角__三角形;当△ABC三边分别为6,8,11时,△ABC为__钝角__三角形;
(2)猜想,当a2+b2__>__c2时,△ABC为锐角三角形;当a2+b2__<__c2时,△ABC为钝角三角形;
(3)判断当a=2,b=4时△ABC的形状,并求出对应的c的取值范围.
解:(3)∵c为最长边,2+4=6,∴4≤c<6,a2+b2=22+42=20,①a2+b2>c2,即c2<20,0<c<2,∴当4≤c<2时,这个三角形是锐角三角形;②a2+b2=c2,即c2=20,c=2,∴当c=2时,这个三角形是直角三角形;③a2+b2<c2,即c2>20,c>2,∴当2<c<6时,这个三角形是钝角三角形
23.(13分)阅读下面材料:
实际问题:如图①,一圆柱的底面半径为5厘米,BC是底面直径,高AB为5厘米,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.
解决方案:
路线1:侧面展开图中的线段AC,如图②所示,
设路线1的长度为l1:则l12=AC2=AB2+BC2=52+(5π)2=25+25π2;
路线2:高线AB+底面直径BC,如图①所示.
设路线2的长度为l2:则l22=(AB+dBC)2=(5+10)2=225.
为比较l1,l2的大小,我们采用“作差法”:
∵l12-l22=25(π2-8)>0,∴l12>l22,∴l1>l2,
小明认为应选择路线2较短.
(1)问题类比:小亮对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1厘米,高AB为5厘米.”请你用上述方法帮小亮比较出l1与l2的大小;
(2)问题拓展:请你帮他们继续研究:在一般情况下,当圆柱的底面半径为r厘米时,高为h厘米,蚂蚁从A点出发沿圆柱表面爬行到点C,当满足什么条件时,选择路线2最短?请说明理由;
(3)问题解决:如图③为2个相同的圆柱紧密排列在一起,高为5厘米,当蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.(注:按上面小明所设计的两条路线方式)
解:(1)如图②.∵圆柱的底面半径为1厘米,高AB为5厘米,
∴路线1:l12=AC2=AB2+BC2=25+π2;
路线2:l2=AB+dBC=5+2=7,l22=(AB+dBC)2=49.
∵l12-l22=25+π2-49=π2-24<0,∴l12
∴路线1:l12=AC2=AB2+BC2=h2+(πr)2=h2+π2r2,路线2:l22=(AB+dBC)2=(h+2r)2,
∴l12-l22=h2+(πr)2-(h+2r)2=r(π2r-4r-4h)=r[(π2-4)r-4h];
∵r恒大于0,∴当(π2-4)r-4h>0,即>时,l12>l22,即此时选择的路2最短
(3)如图③,圆柱的高为5厘米.l12=AC2=AB2+BC2=25+(2πr)2,
l22=(AB+dBC)2=(5+4r)2,由题意,得25+(2πr)2=(5+4r)2,解得r=.
即当圆柱的底面半径r为厘米时,蚂蚁从点A出发沿圆柱表面爬行到C点的两条线段相等
5
