鲁科版(2019)高中 必修 第一册 物理 课件 1.2质点和位移
文档属性
| 名称 | 鲁科版(2019)高中 必修 第一册 物理 课件 1.2质点和位移 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-09 00:00:00 | ||
图片预览










文档简介
质点和位移
一、质点
1.理想模型法:突出问题的_____________,忽略
_____________,将问题简化的方法。?
主要因素
次要因素
2.物体看作质点的条件:
(1)物体的大小和形状对所研究问题的影响可忽略不计。
(2)“物体具有质量”是主要影响因素。
备注:两条件同时满足
3.质点的内涵:用来代替物体的具有_________的点。?
4.质点与物体的关系:质点_________真实的物体,它
是一种___________的物理模型。?
质量
不是
理想化
二、位移
1.位移:
(1)物理意义:描述物体的_____________。?
(2)大小:从初位置指向末位置的有向线段的_______。?
(3)方向:由___________指向___________的箭头的方
向。?
位置变化
长度
初位置
末位置
2.标量和矢量:
(1)标量:只有_________没有_________的物理量。?
(2)矢量:既有_________又有_________的物理量。?
大小
方向
大小
方向
3.路程:
(1)物理意义:描述物体运动轨迹的长短。
(2)内涵:物体运动轨迹的_________。?
长度
4.位移和路程的区别:
关于位移和路程的说法正确的有_________。?
①路程是实际轨迹的长度,没有方向。
②一同学在操场上跑了一圈,用了2分钟,但其位移
为零。
③位移和路程都是有方向的物理量。
④3m的位移比-5m的位移大。
①②
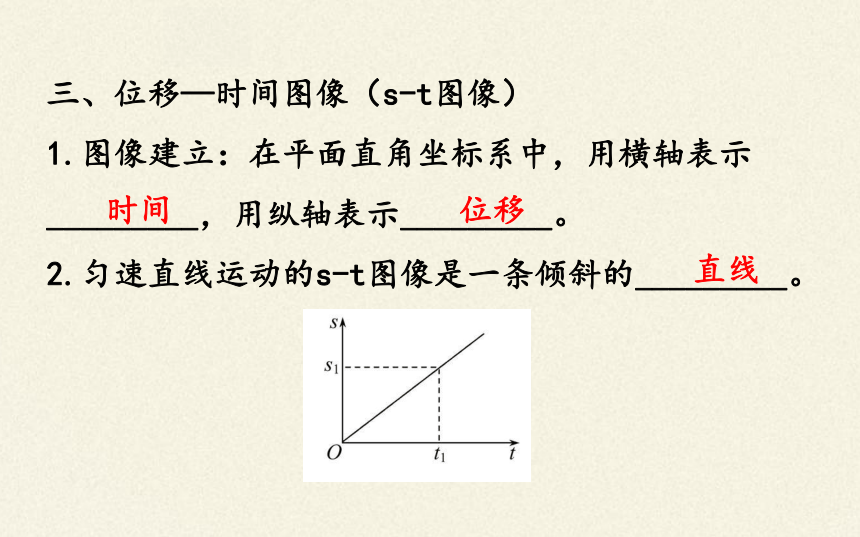
三、位移—时间图像(s-t图像)
1.图像建立:在平面直角坐标系中,用横轴表示
_________,用纵轴表示_________。?
2.匀速直线运动的s-t图像是一条倾斜的_________。?
时间
位移
直线
一、质点模型
1.理想化方法:
(1)质点是一种科学的抽象,是一种理想化的物理模型,是在研究物体运动时,抓住主要因素,忽略次要因素,对实际物体进行的近似处理。
(2)在物理学中,突出问题的主要因素,忽略次要因素,通过对事物的抽象,建立理想化“物理模型”,并将其作为研究对象,是经常采用的一种科学研究方法。
2.质点的三个特点:
(1)没有大小和形状。
(2)具有物体的全部质量。
(3)是一种理想化的物理模型,实际生活中并不存在。
3.把物体看作质点的条件:物体的大小和形状对研究问题的影响可以忽略不计时,不论物体的大小如何,都可把物体看作质点。
【思考·讨论】
情境:如图所示,正在进行中的国际马拉松比赛。
讨论:(1)教练在研究马拉松运动员的摆臂和步幅对速度的影响时,能否把他看成一个“点”?(模型建构)
提示:不能。研究运动员的摆臂和步幅对速度的影响时,他的大小和动作对研究的问题有影响,则不能看作质点。
(2)若研究运动员全程的速度变化时,能否把他看成一个“点”?(科学思维)
提示:能。研究运动员全程的速度变化时,他的大小和动作对研究的问题没有影响,则能看作质点。
【典例示范】
(多选)(2019·福州高一检测)下列说法中正确的是( )
A.研究飞机从成都飞往北京所用的时间时,飞机可视为质点
B.研究直升机螺旋桨的转动情况时,可将直升机视为质点
C.研究火车过长江大桥所用的时间时,可将火车视为质点
D.研究汽车过长江大桥所用的时间时,可将汽车视为质点
【解析】选A、D。A中飞机的大小对所研究的问题无影响,故可视为质点;B中的直升机螺旋桨是直升机的一部分,直升机的大小不能忽略不计,因此直升机不能视为质点;C中火车过桥时,火车的长度会影响火车过桥的时间,故火车不能视为质点;D中汽车过桥时,汽车的长度远远小于桥的长度,汽车的长度对汽车过桥的时间的影响非常小,故汽车可视为质点。
【规律方法】
判断一个物体能否看成质点的思路
(1)判断研究问题的性质,即题中关注的要素是什么,分析、求解的物理量是什么。
(2)假设物体的形状、大小被忽略,思考要求解的物理量、关注的要素是否受影响。
(3)若要求解的物理量不受影响,物体就能被看成质点;若受影响,则物体不能被看成质点。
【素养训练】
1.(2019·南平高一检测)下列关于质点的说法,正确的是( )
A.凡轻小的物体,皆可看作质点
B.只有体积很小的物体才能看作质点
C.质点是一个理想化模型,实际上并不存在,所以,引入这个概念没有多大意义
D.如果物体的形状和大小对所研究的问题属于无关或次要因素时,即可把物体看作质点
【解析】选D。质点是一个理想化模型,实际上并不存
在,引入这个概念可以简化我们分析的问题,不是没
有意义,所以C错误;体积大的物体也可以看作质点,
比如地球,所以B错误;轻小的物体,不一定可以看作
质点,要看它的形状对分析的问题有没有影响,所以A
错误;如果物体的形状和大小对所研究的问题属于无
关或次要因素时,即可把物体看作质点,所以D正确。
2.在以下几个奥运会比赛项目中,研究对象可视为质点的是( )
A.在撑杆跳高比赛中研究运动员手中的支撑杆在支撑地面过程中的转动情况时
B.确定马拉松运动员在比赛中的位置时
C.跆拳道比赛中研究运动员动作时
D.乒乓球比赛中研究乒乓球的旋转时
【解析】选B。能否把某物体视为质点,关键要看忽略物体的大小和形状后,对所研究的问题是否有影响。显然A、C、D项中的研究对象的大小和形状忽略后,所研究的问题将无法继续,故A、C、D项不符合题意;而B项中的研究对象的大小和形状忽略后,所研究的问题不受影响,故B项符合题意。
二、位移和路程的区别与联系
1.矢量和标量的判断:
(1)矢量的表示:
①矢量的图示:用带箭头的线段表示,线段的长短表示矢量的大小,箭头的指向表示矢量的方向。
②同一直线上的矢量:可先建立直线坐标系,在数值前面加上正负号表示矢量的方向,正号表示与坐标系规定的正方向相同,负号则表示与规定的正方向相反。
(2)大小的比较:
标量大小的比较看其自身数值大小,而矢量大小的比较要看其数值的绝对值大小,绝对值大的矢量就大。
如两位移s1=2m,s2=-3m,则两位移的大小关系为|s1|<|s2|。
2.位移和路程的比较:
位 移
路 程
区
别
描述质点的位置变化,是从初位置指向末位置的有向线段
描述质点实际运动轨迹的长度
是矢量,由起始位置指向终止位置的方向为位移的方向,这一矢量线段的长为位移的大小
是标量,只有大小,没有方向,物体运动轨迹的长度即为路程的大小
位 移
路 程
区
别
由质点的初、末位置决定,与质点运动轨迹无关
既与质点的初、末位置有关,也与运动路径有关
位 移
路 程
区
别
例:质点由A点运动到B点,由A点指向B点的有向线段的大小和方向表示质点的位移
例:质点由A点运动到B点,曲线AB的长度即为质点的路程
位 移
路 程
联
系
(1)都是描述质点运动的空间特征的物理量;
(2)都是过程量;
(3)在一个运动过程中,位移的大小不大于相应的路程,只有质点做单向直线运动时,位移的大小才等于路程
【思考·讨论】
情境:如图所示,从济南到郑州可以乘飞机,可以开车走国道。
讨论:(1)两种方式的路程相同吗?(物理观念)
提示:不相同。运动路径不一样。
(2)两种方式的位移相同吗?
提示:相同。初位置指向末位置的有向线段是相同的。
【典例示范】
(2019·泉州高一检测)建筑工地上的起重机把一筐砖先竖直向上提升40m,然后水平移动30m,此过程中关于砖及其路程和位移大小表述正确的是( )
A.砖可视为质点,路程和位移大小都是70m
B.砖不可视为质点,路程和位移大小都是50m
C.砖可视为质点,路程为70m,位移大小为50m
D.砖不可视为质点,路程为50m,位移大小为70m
【解析】选C。当物体的形状、大小对所研究的问题没
有影响或者影响不大时,物体可以看作质点。路程等
于物体运动轨迹的长度,则路程s=40m+30m=70m,
位移大小等于初末位置的距离,x=m=50 m。
则C正确,A、B、D错误。
【误区警示】位移大小不一定等于路程
(1)确定位移时应先确定起点位置和终点位置。
(2)利用几何关系确定其大小,位移大小不一定等于路程。
(3)最终位移的大小不一定是运动过程中的最大值,各段位移的大小之和不一定等于全过程位移的大小。
【素养训练】
1.如图所示,物体从A运动到C,以下说法正确的是( )
A.经1从A运动到C的位移最小
B.经2从A运动到C的位移是曲线
C.经3从A运动到C的位移最大
D.无论从哪条路线运动,位移都相同
【解析】选D。由图看出,三个运动过程物体的起点与终点相同,根据位移是从起点到终点的有向线段可知,位移都相同,位移都是A→C。故D正确,A、B、C错误。
2.(多选)(2019·三明高一检测)如图所示为某学校田径运动场跑道的示意图,其中A点是所有跑步项目的终点,也是400m、800m赛跑的起跑点,B点是100m赛跑的起跑点。在一次校运动会中,甲、乙、丙三位同学分别参加了100m、400m和800m赛跑,则从开始比赛到比赛结束时( )
A.甲的位移最大
B.丙的位移最大
C.乙、丙的路程相等
D.丙的路程最大
【解析】选A、D。甲同学的初、末位置直线距离为
100m,位移大小为100m,路程也是100m;乙同学路
程为400m,但初、末位置重合,位移大小为零;丙同
学路程为800m,初、末位置重合,位移大小也为零,
所以甲的位移最大,丙的路程最大,则A、D正确,B、
C错误。
【补偿训练】
1.从高为2m处以某一初速度竖直向下抛出一个乒乓球,乒乓球在与地面相碰后弹起,上升到高为4m处被接住,则乒乓球在这段运动过程中( )
A.它的位移为2m,方向竖直向上,路程为6m
B.它的位移为6m,方向竖直向上,路程为6m
C.它的位移为2m,方向竖直向上,路程为2m
D.它的位移为6m,方向竖直向下,路程为2m
【解析】选A。从高为2m处以某一初速度竖直向下抛出一个乒乓球,在与地面相碰后弹起,上升到高为4m处被接住,首末位置的距离为2m,所以位移的大小等于2m,方向竖直向上。运动轨迹的长度为2m+4m=6m,所以路程等于6m。故A正确,B、C、D错误。
2.教室在三楼,每天同学们都要从一楼爬到三楼上课。如图所示,假如每层的高度都是3m,楼梯的倾角为45°,一个人从楼梯沿折线从大门走到三楼房门口,他走过的位移是多少?路程又是多少?(把人爬楼过程等效为物体沿坡滑行)
【解析】如题图所示,折线为人的运动轨迹,每个斜梯长为1.5 m,路程
l=4×1.5 m=6 m=8.485m。
初位置在大门口,末位置在房门口,从初位置到末位置的有向线段为位移,所以位移大小为x=2h=6m。
【拓展例题】考查内容:平动或转动的物体能否看作质点
【典例】下列关于质点的说法正确的是( )
A.平动的物体一定可以看成质点,转动的物体不能看成质点
B.各部分运动状态完全一致的物体一定可以看成质点
C.铅球比赛中研究铅球的运动轨迹时,由于铅球的转动不能看成质点
D.平动的物体有时不能看成质点,转动的物体有时可以看成质点
【解析】选D。平动是物体各部分运动状态完全一致的
运动,平动或转动不是判断物体能否看成质点的依据,
平动或转动的物体有时可以看成质点,有时不能看成质点,A、B错误,D正确。研究铅球比赛中铅球的运动轨
迹时,铅球大小对轨迹的影响可以忽略,故铅球可以看
成质点,C错。
【课堂回眸】
谢 谢
一、质点
1.理想模型法:突出问题的_____________,忽略
_____________,将问题简化的方法。?
主要因素
次要因素
2.物体看作质点的条件:
(1)物体的大小和形状对所研究问题的影响可忽略不计。
(2)“物体具有质量”是主要影响因素。
备注:两条件同时满足
3.质点的内涵:用来代替物体的具有_________的点。?
4.质点与物体的关系:质点_________真实的物体,它
是一种___________的物理模型。?
质量
不是
理想化
二、位移
1.位移:
(1)物理意义:描述物体的_____________。?
(2)大小:从初位置指向末位置的有向线段的_______。?
(3)方向:由___________指向___________的箭头的方
向。?
位置变化
长度
初位置
末位置
2.标量和矢量:
(1)标量:只有_________没有_________的物理量。?
(2)矢量:既有_________又有_________的物理量。?
大小
方向
大小
方向
3.路程:
(1)物理意义:描述物体运动轨迹的长短。
(2)内涵:物体运动轨迹的_________。?
长度
4.位移和路程的区别:
关于位移和路程的说法正确的有_________。?
①路程是实际轨迹的长度,没有方向。
②一同学在操场上跑了一圈,用了2分钟,但其位移
为零。
③位移和路程都是有方向的物理量。
④3m的位移比-5m的位移大。
①②
三、位移—时间图像(s-t图像)
1.图像建立:在平面直角坐标系中,用横轴表示
_________,用纵轴表示_________。?
2.匀速直线运动的s-t图像是一条倾斜的_________。?
时间
位移
直线
一、质点模型
1.理想化方法:
(1)质点是一种科学的抽象,是一种理想化的物理模型,是在研究物体运动时,抓住主要因素,忽略次要因素,对实际物体进行的近似处理。
(2)在物理学中,突出问题的主要因素,忽略次要因素,通过对事物的抽象,建立理想化“物理模型”,并将其作为研究对象,是经常采用的一种科学研究方法。
2.质点的三个特点:
(1)没有大小和形状。
(2)具有物体的全部质量。
(3)是一种理想化的物理模型,实际生活中并不存在。
3.把物体看作质点的条件:物体的大小和形状对研究问题的影响可以忽略不计时,不论物体的大小如何,都可把物体看作质点。
【思考·讨论】
情境:如图所示,正在进行中的国际马拉松比赛。
讨论:(1)教练在研究马拉松运动员的摆臂和步幅对速度的影响时,能否把他看成一个“点”?(模型建构)
提示:不能。研究运动员的摆臂和步幅对速度的影响时,他的大小和动作对研究的问题有影响,则不能看作质点。
(2)若研究运动员全程的速度变化时,能否把他看成一个“点”?(科学思维)
提示:能。研究运动员全程的速度变化时,他的大小和动作对研究的问题没有影响,则能看作质点。
【典例示范】
(多选)(2019·福州高一检测)下列说法中正确的是( )
A.研究飞机从成都飞往北京所用的时间时,飞机可视为质点
B.研究直升机螺旋桨的转动情况时,可将直升机视为质点
C.研究火车过长江大桥所用的时间时,可将火车视为质点
D.研究汽车过长江大桥所用的时间时,可将汽车视为质点
【解析】选A、D。A中飞机的大小对所研究的问题无影响,故可视为质点;B中的直升机螺旋桨是直升机的一部分,直升机的大小不能忽略不计,因此直升机不能视为质点;C中火车过桥时,火车的长度会影响火车过桥的时间,故火车不能视为质点;D中汽车过桥时,汽车的长度远远小于桥的长度,汽车的长度对汽车过桥的时间的影响非常小,故汽车可视为质点。
【规律方法】
判断一个物体能否看成质点的思路
(1)判断研究问题的性质,即题中关注的要素是什么,分析、求解的物理量是什么。
(2)假设物体的形状、大小被忽略,思考要求解的物理量、关注的要素是否受影响。
(3)若要求解的物理量不受影响,物体就能被看成质点;若受影响,则物体不能被看成质点。
【素养训练】
1.(2019·南平高一检测)下列关于质点的说法,正确的是( )
A.凡轻小的物体,皆可看作质点
B.只有体积很小的物体才能看作质点
C.质点是一个理想化模型,实际上并不存在,所以,引入这个概念没有多大意义
D.如果物体的形状和大小对所研究的问题属于无关或次要因素时,即可把物体看作质点
【解析】选D。质点是一个理想化模型,实际上并不存
在,引入这个概念可以简化我们分析的问题,不是没
有意义,所以C错误;体积大的物体也可以看作质点,
比如地球,所以B错误;轻小的物体,不一定可以看作
质点,要看它的形状对分析的问题有没有影响,所以A
错误;如果物体的形状和大小对所研究的问题属于无
关或次要因素时,即可把物体看作质点,所以D正确。
2.在以下几个奥运会比赛项目中,研究对象可视为质点的是( )
A.在撑杆跳高比赛中研究运动员手中的支撑杆在支撑地面过程中的转动情况时
B.确定马拉松运动员在比赛中的位置时
C.跆拳道比赛中研究运动员动作时
D.乒乓球比赛中研究乒乓球的旋转时
【解析】选B。能否把某物体视为质点,关键要看忽略物体的大小和形状后,对所研究的问题是否有影响。显然A、C、D项中的研究对象的大小和形状忽略后,所研究的问题将无法继续,故A、C、D项不符合题意;而B项中的研究对象的大小和形状忽略后,所研究的问题不受影响,故B项符合题意。
二、位移和路程的区别与联系
1.矢量和标量的判断:
(1)矢量的表示:
①矢量的图示:用带箭头的线段表示,线段的长短表示矢量的大小,箭头的指向表示矢量的方向。
②同一直线上的矢量:可先建立直线坐标系,在数值前面加上正负号表示矢量的方向,正号表示与坐标系规定的正方向相同,负号则表示与规定的正方向相反。
(2)大小的比较:
标量大小的比较看其自身数值大小,而矢量大小的比较要看其数值的绝对值大小,绝对值大的矢量就大。
如两位移s1=2m,s2=-3m,则两位移的大小关系为|s1|<|s2|。
2.位移和路程的比较:
位 移
路 程
区
别
描述质点的位置变化,是从初位置指向末位置的有向线段
描述质点实际运动轨迹的长度
是矢量,由起始位置指向终止位置的方向为位移的方向,这一矢量线段的长为位移的大小
是标量,只有大小,没有方向,物体运动轨迹的长度即为路程的大小
位 移
路 程
区
别
由质点的初、末位置决定,与质点运动轨迹无关
既与质点的初、末位置有关,也与运动路径有关
位 移
路 程
区
别
例:质点由A点运动到B点,由A点指向B点的有向线段的大小和方向表示质点的位移
例:质点由A点运动到B点,曲线AB的长度即为质点的路程
位 移
路 程
联
系
(1)都是描述质点运动的空间特征的物理量;
(2)都是过程量;
(3)在一个运动过程中,位移的大小不大于相应的路程,只有质点做单向直线运动时,位移的大小才等于路程
【思考·讨论】
情境:如图所示,从济南到郑州可以乘飞机,可以开车走国道。
讨论:(1)两种方式的路程相同吗?(物理观念)
提示:不相同。运动路径不一样。
(2)两种方式的位移相同吗?
提示:相同。初位置指向末位置的有向线段是相同的。
【典例示范】
(2019·泉州高一检测)建筑工地上的起重机把一筐砖先竖直向上提升40m,然后水平移动30m,此过程中关于砖及其路程和位移大小表述正确的是( )
A.砖可视为质点,路程和位移大小都是70m
B.砖不可视为质点,路程和位移大小都是50m
C.砖可视为质点,路程为70m,位移大小为50m
D.砖不可视为质点,路程为50m,位移大小为70m
【解析】选C。当物体的形状、大小对所研究的问题没
有影响或者影响不大时,物体可以看作质点。路程等
于物体运动轨迹的长度,则路程s=40m+30m=70m,
位移大小等于初末位置的距离,x=m=50 m。
则C正确,A、B、D错误。
【误区警示】位移大小不一定等于路程
(1)确定位移时应先确定起点位置和终点位置。
(2)利用几何关系确定其大小,位移大小不一定等于路程。
(3)最终位移的大小不一定是运动过程中的最大值,各段位移的大小之和不一定等于全过程位移的大小。
【素养训练】
1.如图所示,物体从A运动到C,以下说法正确的是( )
A.经1从A运动到C的位移最小
B.经2从A运动到C的位移是曲线
C.经3从A运动到C的位移最大
D.无论从哪条路线运动,位移都相同
【解析】选D。由图看出,三个运动过程物体的起点与终点相同,根据位移是从起点到终点的有向线段可知,位移都相同,位移都是A→C。故D正确,A、B、C错误。
2.(多选)(2019·三明高一检测)如图所示为某学校田径运动场跑道的示意图,其中A点是所有跑步项目的终点,也是400m、800m赛跑的起跑点,B点是100m赛跑的起跑点。在一次校运动会中,甲、乙、丙三位同学分别参加了100m、400m和800m赛跑,则从开始比赛到比赛结束时( )
A.甲的位移最大
B.丙的位移最大
C.乙、丙的路程相等
D.丙的路程最大
【解析】选A、D。甲同学的初、末位置直线距离为
100m,位移大小为100m,路程也是100m;乙同学路
程为400m,但初、末位置重合,位移大小为零;丙同
学路程为800m,初、末位置重合,位移大小也为零,
所以甲的位移最大,丙的路程最大,则A、D正确,B、
C错误。
【补偿训练】
1.从高为2m处以某一初速度竖直向下抛出一个乒乓球,乒乓球在与地面相碰后弹起,上升到高为4m处被接住,则乒乓球在这段运动过程中( )
A.它的位移为2m,方向竖直向上,路程为6m
B.它的位移为6m,方向竖直向上,路程为6m
C.它的位移为2m,方向竖直向上,路程为2m
D.它的位移为6m,方向竖直向下,路程为2m
【解析】选A。从高为2m处以某一初速度竖直向下抛出一个乒乓球,在与地面相碰后弹起,上升到高为4m处被接住,首末位置的距离为2m,所以位移的大小等于2m,方向竖直向上。运动轨迹的长度为2m+4m=6m,所以路程等于6m。故A正确,B、C、D错误。
2.教室在三楼,每天同学们都要从一楼爬到三楼上课。如图所示,假如每层的高度都是3m,楼梯的倾角为45°,一个人从楼梯沿折线从大门走到三楼房门口,他走过的位移是多少?路程又是多少?(把人爬楼过程等效为物体沿坡滑行)
【解析】如题图所示,折线为人的运动轨迹,每个斜梯长为1.5 m,路程
l=4×1.5 m=6 m=8.485m。
初位置在大门口,末位置在房门口,从初位置到末位置的有向线段为位移,所以位移大小为x=2h=6m。
【拓展例题】考查内容:平动或转动的物体能否看作质点
【典例】下列关于质点的说法正确的是( )
A.平动的物体一定可以看成质点,转动的物体不能看成质点
B.各部分运动状态完全一致的物体一定可以看成质点
C.铅球比赛中研究铅球的运动轨迹时,由于铅球的转动不能看成质点
D.平动的物体有时不能看成质点,转动的物体有时可以看成质点
【解析】选D。平动是物体各部分运动状态完全一致的
运动,平动或转动不是判断物体能否看成质点的依据,
平动或转动的物体有时可以看成质点,有时不能看成质点,A、B错误,D正确。研究铅球比赛中铅球的运动轨
迹时,铅球大小对轨迹的影响可以忽略,故铅球可以看
成质点,C错。
【课堂回眸】
谢 谢
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
