数学:同步授课课件 15.4.1《提公因式法》(人教实验版八年级上)
文档属性
| 名称 | 数学:同步授课课件 15.4.1《提公因式法》(人教实验版八年级上) |
|
|
| 格式 | zip | ||
| 文件大小 | 576.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-24 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
15.4 因式分解
15.4.1 提公因式法
整式的乘法
计算下列各式:
x(x+1)=
(x+1)(x-1)=
x2 + x
x2-1
温故知新
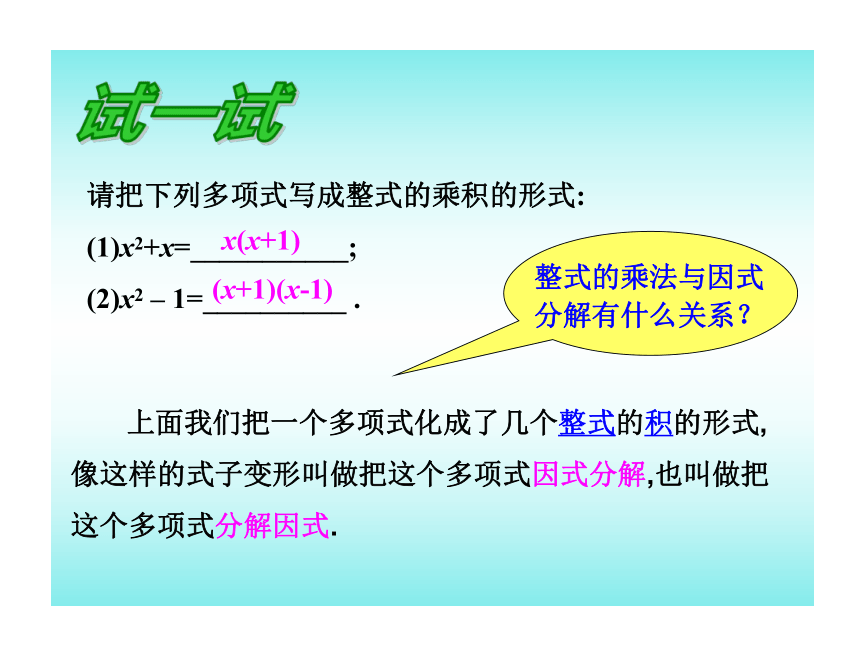
请把下列多项式写成整式的乘积的形式:
(1)x2+x=___________;
(2)x2 – 1=__________ .
x(x+1)
(x+1)(x-1)
上面我们把一个多项式化成了几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.
整式的乘法与因式分解有什么关系?
x2-1
因式分解
整式乘法
(x+1)(x-1)
因式分解与整式乘法是相反方向的变形
由m(a+b+c) = ma+mb+mc可得:ma+mb+mc =m(a+b+c)
这样就把ma+mb+mc分解成两个因式乘积的形式,其中一个因式是各项的公因式m,另一个因式(a+b+c)是ma+mb+mc除以 m所得的商,像这种分解因式的方法叫做 ____________ .
它的各项都有一个公共的因式m,我们把因式m叫做这个多项式的 _________ .
ma+mb+mc
公因式
提公因式法
例1 把8a3b2 + 12ab3c 分解因式.
分析:找公因式
1、系数的最大公约数 4
2、找相同字母 ab
3、相同字母的最低指数 a1b2
公因式为:4ab2
典例解析
解:8a3b2+12ab3c
=4ab2 2a2+4ab2 3bc
=4ab2(2a2+3bc)
解:a(x-3)+2b(x-3)
=(x-3)(a+2b)
例2:把a(x-3)+2b(x-3)分解因式
分析:这个多项式整体而言可分为两大项,即a(x-3)与2b(x-3),每项中都含有(x-3),因此可以把(x-3)作为公因式提出来.
例3:把下列各式分解因式:
(1)a(x-y)+b(y-x);
分析:虽然a(x-y)与b(y-x)看上去没有公因式,但仔细观察可以看出(x-y)与(y-x)是互为相反数,如果把其中一个提取一个“-”号,则可以出现公因式,如:y-x=-(x-y)
解:(1)a(x-y)+b(y-x)
=a(x-y)-b(x-y)
=(x-y)(a-b)
解:(2)6(m-n)3-12(n-m)2
=6(m-n)3-12[-(m-n)]2
=6(m-n)3-12(m-n)2
=6(m-n)2(m-n-2).
(2)6(m-n)3-12(n-m)2
典例解析
1、填空
请在下列各式等号右边的括号前填入“+”或“-”号,使等式成立:
(1)2-a=______(a-2);
(2)y-x=_____(x-y);
(3)b+a=______(a+b);
(4)(b-a)2=_____(a-b)2;
(5)-m-n=_____(m+n);
(6)-s2+t2=_____(s2-t2).
-
-
+
+
-
-
巩固训练
2.写出下列多项式各项的公因式.
(1)ma+mb
(2)4kx-8ky
(3)5y3+20y2
(4)a2b-2ab2+ab
m
4k
5y2
ab
3.把下列各式分解因式
(1)8x-72
(2)a2b-5ab
(3)4m3-6m2
(4)a2b-5ab+9b
(5)-a2+ab-ac
(6)-2x3+4x2-2x
=8(x-9)
=ab(a-5)
=2m2(2m-3)
=b(a2-5a+9)
=-(a2-ab+ac)=-a(a-b+c)
=-(2x3-4x2+2x)=-2x(x2-2x+1)
解:原式=(a+b-c)(a-b+c)-(b-a+c)(a-b+c)
=(a-b+c)[(a+b-c)-(b-a+c)]
=(a-b+c)(a+b-c-b+a-c)
=(a-b+c)(2a-2c)
=2(a-b+c)(a-c)
把(a+b-c)(a-b+c)+(b-a+c)·(b-a-c)分解因式
能力挑战
把一个多项式化成了几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.
提公因式法
分解因式的方法:
注意符号变化
课堂小结
15.4 因式分解
15.4.1 提公因式法
整式的乘法
计算下列各式:
x(x+1)=
(x+1)(x-1)=
x2 + x
x2-1
温故知新
请把下列多项式写成整式的乘积的形式:
(1)x2+x=___________;
(2)x2 – 1=__________ .
x(x+1)
(x+1)(x-1)
上面我们把一个多项式化成了几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.
整式的乘法与因式分解有什么关系?
x2-1
因式分解
整式乘法
(x+1)(x-1)
因式分解与整式乘法是相反方向的变形
由m(a+b+c) = ma+mb+mc可得:ma+mb+mc =m(a+b+c)
这样就把ma+mb+mc分解成两个因式乘积的形式,其中一个因式是各项的公因式m,另一个因式(a+b+c)是ma+mb+mc除以 m所得的商,像这种分解因式的方法叫做 ____________ .
它的各项都有一个公共的因式m,我们把因式m叫做这个多项式的 _________ .
ma+mb+mc
公因式
提公因式法
例1 把8a3b2 + 12ab3c 分解因式.
分析:找公因式
1、系数的最大公约数 4
2、找相同字母 ab
3、相同字母的最低指数 a1b2
公因式为:4ab2
典例解析
解:8a3b2+12ab3c
=4ab2 2a2+4ab2 3bc
=4ab2(2a2+3bc)
解:a(x-3)+2b(x-3)
=(x-3)(a+2b)
例2:把a(x-3)+2b(x-3)分解因式
分析:这个多项式整体而言可分为两大项,即a(x-3)与2b(x-3),每项中都含有(x-3),因此可以把(x-3)作为公因式提出来.
例3:把下列各式分解因式:
(1)a(x-y)+b(y-x);
分析:虽然a(x-y)与b(y-x)看上去没有公因式,但仔细观察可以看出(x-y)与(y-x)是互为相反数,如果把其中一个提取一个“-”号,则可以出现公因式,如:y-x=-(x-y)
解:(1)a(x-y)+b(y-x)
=a(x-y)-b(x-y)
=(x-y)(a-b)
解:(2)6(m-n)3-12(n-m)2
=6(m-n)3-12[-(m-n)]2
=6(m-n)3-12(m-n)2
=6(m-n)2(m-n-2).
(2)6(m-n)3-12(n-m)2
典例解析
1、填空
请在下列各式等号右边的括号前填入“+”或“-”号,使等式成立:
(1)2-a=______(a-2);
(2)y-x=_____(x-y);
(3)b+a=______(a+b);
(4)(b-a)2=_____(a-b)2;
(5)-m-n=_____(m+n);
(6)-s2+t2=_____(s2-t2).
-
-
+
+
-
-
巩固训练
2.写出下列多项式各项的公因式.
(1)ma+mb
(2)4kx-8ky
(3)5y3+20y2
(4)a2b-2ab2+ab
m
4k
5y2
ab
3.把下列各式分解因式
(1)8x-72
(2)a2b-5ab
(3)4m3-6m2
(4)a2b-5ab+9b
(5)-a2+ab-ac
(6)-2x3+4x2-2x
=8(x-9)
=ab(a-5)
=2m2(2m-3)
=b(a2-5a+9)
=-(a2-ab+ac)=-a(a-b+c)
=-(2x3-4x2+2x)=-2x(x2-2x+1)
解:原式=(a+b-c)(a-b+c)-(b-a+c)(a-b+c)
=(a-b+c)[(a+b-c)-(b-a+c)]
=(a-b+c)(a+b-c-b+a-c)
=(a-b+c)(2a-2c)
=2(a-b+c)(a-c)
把(a+b-c)(a-b+c)+(b-a+c)·(b-a-c)分解因式
能力挑战
把一个多项式化成了几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.
提公因式法
分解因式的方法:
注意符号变化
课堂小结
