北师大版数学八年级上册7.1 为什么要证明 课件(34张)
文档属性
| 名称 | 北师大版数学八年级上册7.1 为什么要证明 课件(34张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 16:45:40 | ||
图片预览











文档简介
7.1 为什么要证明
a
b
c
d
现实生活中,我们常用观察的方法来了解世界.数学学习中,我们也用观察、实验、归纳的方法得出了很多结论.观察、实验、归纳的方法得到的结论一定正确吗?如果不是,那么,用什么方法证明它呢?
导入新知
1.了解推理的意义,知道要判断一个数学结论是否正确,必须进行推理.
2. 会用实验验证、举出反例、推理等方法简单地验证一个数学结论是否正确.
素养目标
3. 培养合作交流并探讨的学习品质,培养用科学的态度审视在数学活动中遇到的不确定结论的习惯.
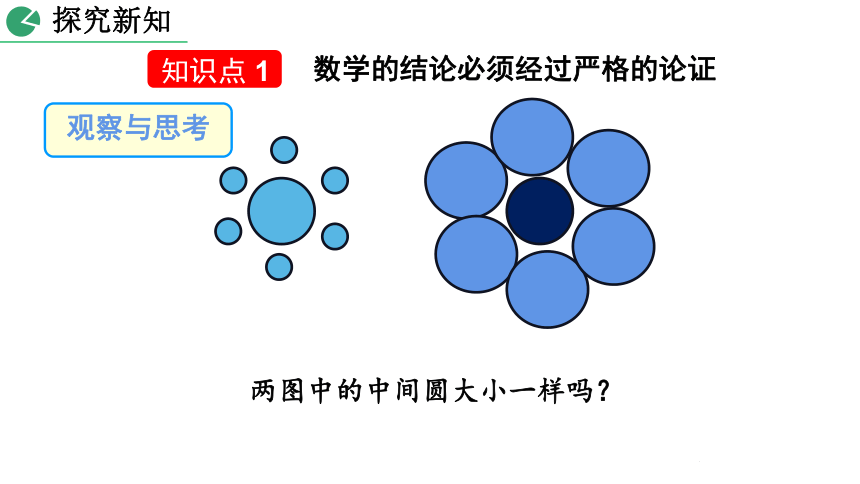
观察与思考
两图中的中间圆大小一样吗?
探究新知
知识点 1
数学的结论必须经过严格的论证
探究新知
线是直还是曲?
观察与思考
图中的四边形是正方形吗?
探究新知
观察与思考
是静还是动?
探究新知
观察与思考
平行线:不敢相信图中的横线是平行的,不过它们就是平行线!
你觉得观察得到的结论正确吗?
探究新知
观察与思考
判断一个数学结论是否正确,仅观察、猜想、
实验还不够;
必须经过一步一步、 有根有据的证明.
请举例说明,你用到过的推理.
探究新知
做一做
如图,假如用一根比地球的赤道长1m的铁丝将地球赤道围起来,那么铁丝与地球赤道之间的间隙能有多大?(地球看成球形)能放进一个红枣吗?能放进一个拳头吗?
解:设赤道周长为C,铁丝与地球赤道
之间的间隙为 :
它们的间隙不仅能放进一个红枣,而且也能放进一个拳头.
探究新知
费 马
对于所有自然数n, 的值都是质数.
当n=0,1,2,3,4时,
= 3,5,17,257,65 537
都是质数.
欧 拉
当n=5时,
= 4 294 967 297=
641×6 700 417
举出反例是检验错误数学结论的有效方法.
大数学家也有失误
探究新知
这个故事告诉我们:
1. 学习欧拉的求实精神与严谨的科学态度.
2.没有严格的推理,仅由若干特例归纳、猜测的结论可能潜藏着错误,未必正确.
3.要证明一个结论是错误的,举反例就是一种常用方法.
探究新知
归纳总结
例1 先观察再验证.
(1)图①中实线是直的还是弯曲的?
(2)图②中两条线段a与b哪一条更长?
(3)图③中的直线AB与直线CD平行吗?
知识点 2
检验数学结论的常用方法
探究新知
素养考点 1
实验验证法
解:观察可能得出的结论是:
①实线是弯曲的;
②a更长一些;
③AB与DC不平行.
而我们用科学的方法验证后发现:
①实线是直的;
② a与b一样长;
③ AB平行于CD.
探究新知
归纳总结
有时视觉受周围环境的影响,往往误导我们,让我们得出错误的结论,所以仅靠经验、观察是不够的,只有通过科学的实验进行严格的推理,才能得出最准确的结论.
探究新知
a = b
巩固练习
图中两条线段a与b的长度相等吗?
变式训练
变式训练
a
b
a
b
考考你的眼力
线段a与线段b哪个
比较长?
a
b
c
d
谁与线段d在
一条直线上?
巩固练习
变式训练
a
b
a
b
c
d
检验你的结论
a=b
巩固练习
例2 当n为正整数时,代数式(n2-5n+5)2的值都等于1吗?
解:当n=1时,(n2-5n+5)2=12=1;
当n=2时,(n2-5n+5)2=(-1)2=1;
当n=3时,(n2-5n+5)2=(-1)2=1;
当n=4时,(n2-5n+5)2=12=1;
当n=5时,(n2-5n+5)2=52=25≠1.
所以当n为正整数时,(n2-5n+5)2的值不一定等于1.
探究新知
方法总结:验证特例是判断一个结论错误的最好方法.
素养考点 2
推理证明法
当n=0,1,2,3,4,5时,代数式n2 -n+11的值是质数吗?
你能否得到结论:对于所有自然数n,代数式n2-n+11的值都是质数?
n
0
1
2
3
4
5
n2 -n+11
11
11
13
17
23
31
代数式n2-n+11的值都是质数吗?
巩固练习
n
6
7
8
9
10
11
n2 -n+11
41
53
67
83
101
121
对于所有自然数n,代数式n2-n+11的值不一定都是质数.
变式训练
例3 如图,从点O出发作出四条射线OA,OB,OC,OD,已知OA⊥OC,OB⊥OD.
(1)若∠BOC=30°,求∠AOB和∠COD的度数.
(2)若∠BOC=54°,求∠AOB和∠COD的度数.
(3)由(1)、(2)你发现了什么?
(4)你能肯定上述的发现吗?
分析:图中∠AOB,∠COD均与∠BOC互余,根据角的和、差关系,可求得∠AOB与∠COD的度数.通过计算发现∠AOB=∠COD,于是可以归纳∠AOB=∠COD.
探究新知
解:(1)因为OA⊥OC,OB⊥OD,
所以∠AOC=∠BOD=90°.
因为∠BOC=30°,
所以∠AOB=∠AOC-∠BOC
=90°-30°=60°,
∠COD=∠BOD-∠BOC
=90°-30°=60°.
例3 如图,从点O出发作出四条射线OA,OB,OC,OD,已知OA⊥OC,OB⊥OD.
(1)若∠BOC=30°,求∠AOB和∠COD的度数;
探究新知
解:(2)∠AOB=∠AOC-∠BOC
=90°-54°=36°,
∠COD=∠BOD-∠BOC
=90°-54°=36°.
例3 如图,从点O出发作出四条射线OA,OB,OC,OD,已知OA⊥OC,OB⊥OD.
(2)若∠BOC=54°,求∠AOB和∠COD的度数;
探究新知
解:(3)由(1)、(2)可发现:
∠AOB=∠COD.
例3 如图,从点O出发作出四条射线OA,OB,OC,OD,已知OA⊥OC,OB⊥OD.
(3)由(1)、(2)你发现了什么?
(4)你能肯定上述的发现吗?
探究新知
(4)因为 ∠AOB+∠BOC=∠AOC=90°,
∠BOC+∠COD=∠BOD=90°
所以∠AOB+∠BOC=∠BOC+∠COD.
所以∠AOB=∠COD.
方法总结:检验数学结论具体经历的过程是:
观察、度量、实验→猜想归纳→结论→推理→正确结论.
如图,在△ABC中,点D,E分别是AB,AC的中点.连接DE,DE与BC有怎样的位置关系?有怎样的数量关系?先猜一猜,再设法检验你的猜想.你能肯定你的结论对所有△ABC都成立吗?与同伴进行交流.
解:DE与BC平行,DE的长度等于BC
的一半.通过测量检验这个结论是正确的.这个结论对所有三角形都成立.
巩固练习
变式训练
1.(2018?淄博)甲、乙、丙、丁4人进行乒乓球单循环比赛(每两个人都要比赛一场),结果甲胜了丁,并且甲、乙、丙胜的场次相同,则丁胜的场次是( )
A. 3 B. 2 C. 1 D.0
连接中考
D
2.(2018?广安)为了从2018枚外形相同的金蛋中找出唯一的有奖金蛋,检查员将这些金蛋按1﹣2018的顺序进行标号.第一次先取出编号为单数的金蛋,发现其中没有有奖金蛋,他将剩下的金蛋在原来的位置上又按1﹣1009编了号(即原来的2号变为1号,原来的4号变为2号……原来的2018号变为1009号),又从中取出新的编号为单数的金蛋进行检验,仍没有发现有奖金蛋……如此下去,检查到最后一枚金蛋才是有奖金蛋,问这枚有奖金蛋最初的编号是_______.
1024
1.下列结论中你能肯定的是( )
A.今天下雨,明天必然还下雨
B.三个连续整数的积一定能被6整除
C.小明在数学竞赛中一定能获奖
D.两张相片看起来佷像,则肯定照的是同一个人
2.顺次连接等腰梯形四边中点,所得到的四边形是( )
A.平行四边形 B.矩形 C.正方形 D.菱形
B
D
课堂检测
基础巩固题
3.下列问题用到推理的是( )
A.根据a=10,b=10,得到a=b
B.观察得到三角形有三个角
C.老师告诉我们关于金字塔的许多奥秘
D.由经验可知过两点有且只有一条直线
A
基础巩固题
课堂检测
4.当x为任意实数时,x2+4x+5的值都大于零吗?
解:x2+4x+5=x2+4x+4+1=(x+2)2+1.
因为(x+2)2≥0,所以(x+2)2+1>0.
所以当x为任意实数时,x2+4x+5的值都大于零.
课堂检测
5.当n为正整数时,n2+3n+1的值一定是质数吗?
解:不是,当n=6时, n2+3n+1=55不是质数.
基础巩固题
6. 如图,有A,B,C,D,E,F六个人坐在一张圆桌周围共进午餐.已知C坐在①号位,E和C相隔一人且坐在C的右边,D坐在A的对面,B与F相隔一人且坐在F的右边,F与A不相邻.请问A,B,C,D,E,F各坐在哪个位置?
C ①
⑥
③
④
②
⑤
E
A
F
D
B
基础巩固题
课堂检测
如图,在△ABC中,已知∠ACB=90°,CA=CB,AD⊥CE于点D,BE⊥CE于点E.求证:AD=CE.
解:因为∠ACB=90°,
所以∠BCE+∠ACD=90°(互余的定义).
因为AD⊥CE,
所以∠ADC=90°(垂直的定义).
所以∠ACD+∠CAD=90°(直角三角形两锐角互余).
所以∠CAD=∠BCE(同角的余角相等).
因为BE⊥CE,所以∠CEB=∠ADC=90°(垂直的定义).
因为CA=CB,所以△ACD≌△CBE(AAS).
所以AD=CE(全等三角形的对应边相等).
能力提升题
课堂检测
从2开始,连续的偶数相加,和的情况如下:
2+4=6=2×3;
2+4+6=12=3×4;
2+4+6+8=20=4×5;……
(1)请推测从2开始,n个连续偶数相加,和是多少.
(2)取n=6,验证(1)的结论是否正确.
课堂检测
解:(1)2+4+6+…+2n=n(n+1).
(2)当n=6时,按规律应是2+4+6+8+10+12=42=6×7,按(1)的结论是n(n+1)=6×(6+1),所以(1)的结论是正确的.
拓广探索题
为什么要证明
数学结论必须经过严格的论证
实验验证
举出反例
推理证明
论证方法
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
a
b
c
d
现实生活中,我们常用观察的方法来了解世界.数学学习中,我们也用观察、实验、归纳的方法得出了很多结论.观察、实验、归纳的方法得到的结论一定正确吗?如果不是,那么,用什么方法证明它呢?
导入新知
1.了解推理的意义,知道要判断一个数学结论是否正确,必须进行推理.
2. 会用实验验证、举出反例、推理等方法简单地验证一个数学结论是否正确.
素养目标
3. 培养合作交流并探讨的学习品质,培养用科学的态度审视在数学活动中遇到的不确定结论的习惯.
观察与思考
两图中的中间圆大小一样吗?
探究新知
知识点 1
数学的结论必须经过严格的论证
探究新知
线是直还是曲?
观察与思考
图中的四边形是正方形吗?
探究新知
观察与思考
是静还是动?
探究新知
观察与思考
平行线:不敢相信图中的横线是平行的,不过它们就是平行线!
你觉得观察得到的结论正确吗?
探究新知
观察与思考
判断一个数学结论是否正确,仅观察、猜想、
实验还不够;
必须经过一步一步、 有根有据的证明.
请举例说明,你用到过的推理.
探究新知
做一做
如图,假如用一根比地球的赤道长1m的铁丝将地球赤道围起来,那么铁丝与地球赤道之间的间隙能有多大?(地球看成球形)能放进一个红枣吗?能放进一个拳头吗?
解:设赤道周长为C,铁丝与地球赤道
之间的间隙为 :
它们的间隙不仅能放进一个红枣,而且也能放进一个拳头.
探究新知
费 马
对于所有自然数n, 的值都是质数.
当n=0,1,2,3,4时,
= 3,5,17,257,65 537
都是质数.
欧 拉
当n=5时,
= 4 294 967 297=
641×6 700 417
举出反例是检验错误数学结论的有效方法.
大数学家也有失误
探究新知
这个故事告诉我们:
1. 学习欧拉的求实精神与严谨的科学态度.
2.没有严格的推理,仅由若干特例归纳、猜测的结论可能潜藏着错误,未必正确.
3.要证明一个结论是错误的,举反例就是一种常用方法.
探究新知
归纳总结
例1 先观察再验证.
(1)图①中实线是直的还是弯曲的?
(2)图②中两条线段a与b哪一条更长?
(3)图③中的直线AB与直线CD平行吗?
知识点 2
检验数学结论的常用方法
探究新知
素养考点 1
实验验证法
解:观察可能得出的结论是:
①实线是弯曲的;
②a更长一些;
③AB与DC不平行.
而我们用科学的方法验证后发现:
①实线是直的;
② a与b一样长;
③ AB平行于CD.
探究新知
归纳总结
有时视觉受周围环境的影响,往往误导我们,让我们得出错误的结论,所以仅靠经验、观察是不够的,只有通过科学的实验进行严格的推理,才能得出最准确的结论.
探究新知
a = b
巩固练习
图中两条线段a与b的长度相等吗?
变式训练
变式训练
a
b
a
b
考考你的眼力
线段a与线段b哪个
比较长?
a
b
c
d
谁与线段d在
一条直线上?
巩固练习
变式训练
a
b
a
b
c
d
检验你的结论
a=b
巩固练习
例2 当n为正整数时,代数式(n2-5n+5)2的值都等于1吗?
解:当n=1时,(n2-5n+5)2=12=1;
当n=2时,(n2-5n+5)2=(-1)2=1;
当n=3时,(n2-5n+5)2=(-1)2=1;
当n=4时,(n2-5n+5)2=12=1;
当n=5时,(n2-5n+5)2=52=25≠1.
所以当n为正整数时,(n2-5n+5)2的值不一定等于1.
探究新知
方法总结:验证特例是判断一个结论错误的最好方法.
素养考点 2
推理证明法
当n=0,1,2,3,4,5时,代数式n2 -n+11的值是质数吗?
你能否得到结论:对于所有自然数n,代数式n2-n+11的值都是质数?
n
0
1
2
3
4
5
n2 -n+11
11
11
13
17
23
31
代数式n2-n+11的值都是质数吗?
巩固练习
n
6
7
8
9
10
11
n2 -n+11
41
53
67
83
101
121
对于所有自然数n,代数式n2-n+11的值不一定都是质数.
变式训练
例3 如图,从点O出发作出四条射线OA,OB,OC,OD,已知OA⊥OC,OB⊥OD.
(1)若∠BOC=30°,求∠AOB和∠COD的度数.
(2)若∠BOC=54°,求∠AOB和∠COD的度数.
(3)由(1)、(2)你发现了什么?
(4)你能肯定上述的发现吗?
分析:图中∠AOB,∠COD均与∠BOC互余,根据角的和、差关系,可求得∠AOB与∠COD的度数.通过计算发现∠AOB=∠COD,于是可以归纳∠AOB=∠COD.
探究新知
解:(1)因为OA⊥OC,OB⊥OD,
所以∠AOC=∠BOD=90°.
因为∠BOC=30°,
所以∠AOB=∠AOC-∠BOC
=90°-30°=60°,
∠COD=∠BOD-∠BOC
=90°-30°=60°.
例3 如图,从点O出发作出四条射线OA,OB,OC,OD,已知OA⊥OC,OB⊥OD.
(1)若∠BOC=30°,求∠AOB和∠COD的度数;
探究新知
解:(2)∠AOB=∠AOC-∠BOC
=90°-54°=36°,
∠COD=∠BOD-∠BOC
=90°-54°=36°.
例3 如图,从点O出发作出四条射线OA,OB,OC,OD,已知OA⊥OC,OB⊥OD.
(2)若∠BOC=54°,求∠AOB和∠COD的度数;
探究新知
解:(3)由(1)、(2)可发现:
∠AOB=∠COD.
例3 如图,从点O出发作出四条射线OA,OB,OC,OD,已知OA⊥OC,OB⊥OD.
(3)由(1)、(2)你发现了什么?
(4)你能肯定上述的发现吗?
探究新知
(4)因为 ∠AOB+∠BOC=∠AOC=90°,
∠BOC+∠COD=∠BOD=90°
所以∠AOB+∠BOC=∠BOC+∠COD.
所以∠AOB=∠COD.
方法总结:检验数学结论具体经历的过程是:
观察、度量、实验→猜想归纳→结论→推理→正确结论.
如图,在△ABC中,点D,E分别是AB,AC的中点.连接DE,DE与BC有怎样的位置关系?有怎样的数量关系?先猜一猜,再设法检验你的猜想.你能肯定你的结论对所有△ABC都成立吗?与同伴进行交流.
解:DE与BC平行,DE的长度等于BC
的一半.通过测量检验这个结论是正确的.这个结论对所有三角形都成立.
巩固练习
变式训练
1.(2018?淄博)甲、乙、丙、丁4人进行乒乓球单循环比赛(每两个人都要比赛一场),结果甲胜了丁,并且甲、乙、丙胜的场次相同,则丁胜的场次是( )
A. 3 B. 2 C. 1 D.0
连接中考
D
2.(2018?广安)为了从2018枚外形相同的金蛋中找出唯一的有奖金蛋,检查员将这些金蛋按1﹣2018的顺序进行标号.第一次先取出编号为单数的金蛋,发现其中没有有奖金蛋,他将剩下的金蛋在原来的位置上又按1﹣1009编了号(即原来的2号变为1号,原来的4号变为2号……原来的2018号变为1009号),又从中取出新的编号为单数的金蛋进行检验,仍没有发现有奖金蛋……如此下去,检查到最后一枚金蛋才是有奖金蛋,问这枚有奖金蛋最初的编号是_______.
1024
1.下列结论中你能肯定的是( )
A.今天下雨,明天必然还下雨
B.三个连续整数的积一定能被6整除
C.小明在数学竞赛中一定能获奖
D.两张相片看起来佷像,则肯定照的是同一个人
2.顺次连接等腰梯形四边中点,所得到的四边形是( )
A.平行四边形 B.矩形 C.正方形 D.菱形
B
D
课堂检测
基础巩固题
3.下列问题用到推理的是( )
A.根据a=10,b=10,得到a=b
B.观察得到三角形有三个角
C.老师告诉我们关于金字塔的许多奥秘
D.由经验可知过两点有且只有一条直线
A
基础巩固题
课堂检测
4.当x为任意实数时,x2+4x+5的值都大于零吗?
解:x2+4x+5=x2+4x+4+1=(x+2)2+1.
因为(x+2)2≥0,所以(x+2)2+1>0.
所以当x为任意实数时,x2+4x+5的值都大于零.
课堂检测
5.当n为正整数时,n2+3n+1的值一定是质数吗?
解:不是,当n=6时, n2+3n+1=55不是质数.
基础巩固题
6. 如图,有A,B,C,D,E,F六个人坐在一张圆桌周围共进午餐.已知C坐在①号位,E和C相隔一人且坐在C的右边,D坐在A的对面,B与F相隔一人且坐在F的右边,F与A不相邻.请问A,B,C,D,E,F各坐在哪个位置?
C ①
⑥
③
④
②
⑤
E
A
F
D
B
基础巩固题
课堂检测
如图,在△ABC中,已知∠ACB=90°,CA=CB,AD⊥CE于点D,BE⊥CE于点E.求证:AD=CE.
解:因为∠ACB=90°,
所以∠BCE+∠ACD=90°(互余的定义).
因为AD⊥CE,
所以∠ADC=90°(垂直的定义).
所以∠ACD+∠CAD=90°(直角三角形两锐角互余).
所以∠CAD=∠BCE(同角的余角相等).
因为BE⊥CE,所以∠CEB=∠ADC=90°(垂直的定义).
因为CA=CB,所以△ACD≌△CBE(AAS).
所以AD=CE(全等三角形的对应边相等).
能力提升题
课堂检测
从2开始,连续的偶数相加,和的情况如下:
2+4=6=2×3;
2+4+6=12=3×4;
2+4+6+8=20=4×5;……
(1)请推测从2开始,n个连续偶数相加,和是多少.
(2)取n=6,验证(1)的结论是否正确.
课堂检测
解:(1)2+4+6+…+2n=n(n+1).
(2)当n=6时,按规律应是2+4+6+8+10+12=42=6×7,按(1)的结论是n(n+1)=6×(6+1),所以(1)的结论是正确的.
拓广探索题
为什么要证明
数学结论必须经过严格的论证
实验验证
举出反例
推理证明
论证方法
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
