华师大版数学九年级上册第24章 解直角三角形达标测试卷(word版 含答案)
文档属性
| 名称 | 华师大版数学九年级上册第24章 解直角三角形达标测试卷(word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 159.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 20:27:00 | ||
图片预览



文档简介
第24章达标测试卷
一、选择题(每题3分,共30分)
1.在Rt△ABC中,cosA=,那么∠A的度数为( )
A.45° B.60° C.30° D.无法确定
2.在Rt△ABC中,∠C=90°,若AB=3BC,则tanA的值是( )
A. B.3 C.2 D.
3.已知锐角α,且sinα=cos37°,则α等于( )
A.37° B.63° C.53° D.45°
4.如图,在△ABC中,AB=3,BC=2,∠B=60°,则△ABC的面积等于( )
A. B. C. D.3
5.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A.变小 B.不变 C.变大 D.无法判断
6.点M(-sin 60°,cos 60°)关于x轴对称的点的坐标是( )
A. B. C. D.
7.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cos α=,AB=4,则AC的长为( )
A.3 B. C. D.
8.已知45°<∠A<90°,则下列各式成立的是( )
A.sin A=cos A B.sin A>cos A C.sin A>tan A D.sin A9.某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就会有危险,那么梯子的长至少为( )
A.8米 B.8 米 C.米 D.米
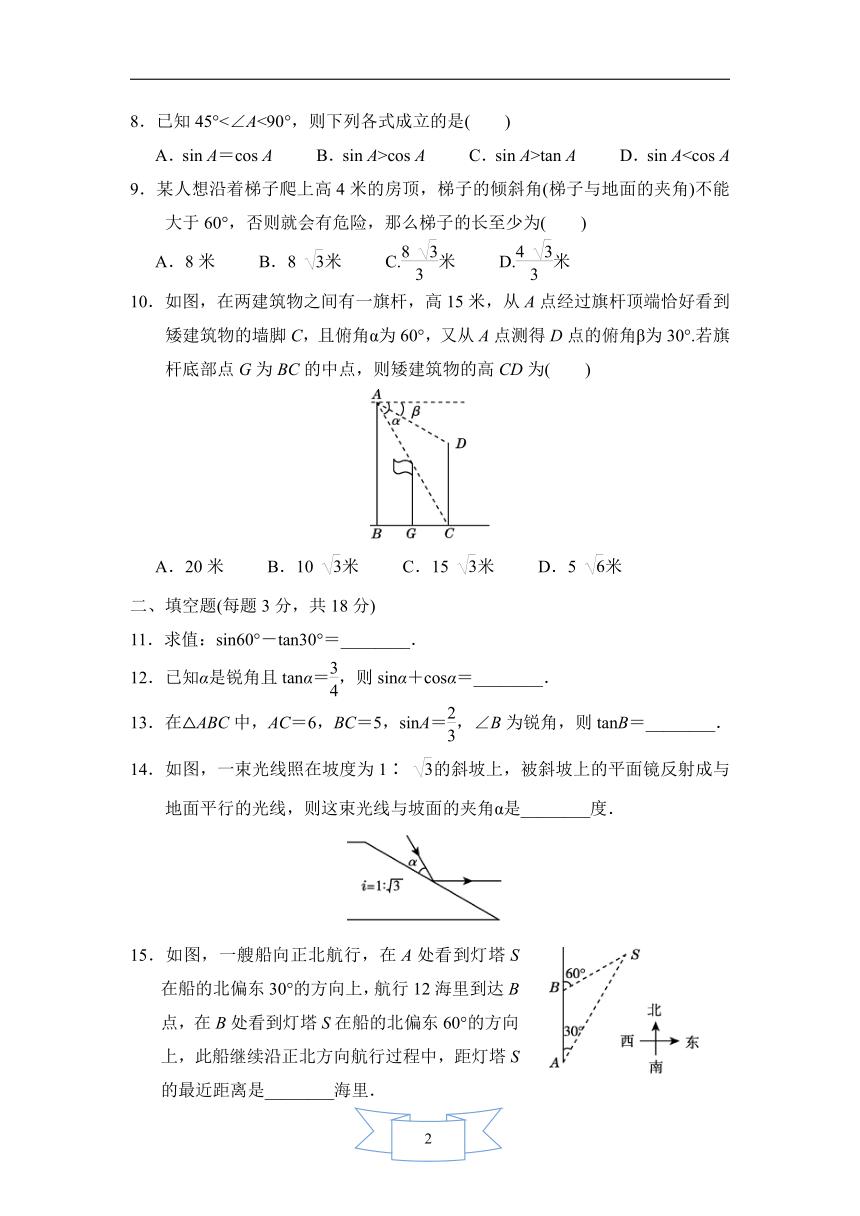
10.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶端恰好看到矮建筑物的墙脚C,且俯角α为60°,又从A点测得D点的俯角β为30°.若旗杆底部点G为BC的中点,则矮建筑物的高CD为( )
A.20米 B.10 米 C.15 米 D.5 米
二、填空题(每题3分,共18分)
11.求值:sin60°-tan30°=________.
12.已知α是锐角且tanα=,则sinα+cosα=________.
13.在△ABC中,AC=6,BC=5,sinA=,∠B为锐角,则tanB=________.
14.如图,一束光线照在坡度为1∶ 的斜坡上,被斜坡上的平面镜反射成与地面平行的光线,则这束光线与坡面的夹角α是________度.
15.如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中,距灯塔S的最近距离是________海里.
16.如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=________.
三、解答题(17~20题每题8分,21~22题每题10分,共52分)
17.计算下列各题:
(1) cos 30°-2tan 45°+sin 30°;
(2)·cos260°--.
18.如图,在△ABC中,∠BCA=135°,AC=2 ,BC=4,求AB的长.
19.如图,△ABC中,∠B=45°,AB=3 ,D是BC中点,tanC=.求:
(1)BC的长;
(2)sin∠ADB.
20.如图,某次“海上联合”反潜演习中,我军舰A测得潜艇C的俯角为30°.位于军舰A正上方1 000米的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数.参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5, ≈1.7)
21.定义:我们把∠A的对边与∠C 的对边的比叫做∠A的邻弦,记作thi A,即thi A==.请解答下列问题:
已知:在△ABC中,∠C=30°.
(1)若∠A=45°,求thi A的值;
(2)若thi A= ,则∠A=________;
(3)若∠A是锐角,探究thi A与sinA的数量关系.
22.如图,在梯形ABCD中,AB∥DC,∠BCD=90°,且AB=1,BC=2,
tan ∠ADC=2.
(1)求证:DC=BC;
(2)E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
(3)在(2)的条件下,当BE∶CE=1∶2,∠BEC=135°时,求sin ∠BFE.
答案
一、1.B 2.D 3.C
4.A 点拨:过点C作AB的垂线,垂足为D,则CD=BCsinB,△ABC的面积S=AB·BCsinB=×3×2×sin60°= .
5.B 点拨:连结OP,∵∠AOB=90°,P为AB中点,设AB=2a,则OP=AB=a,即在木棍滑动的过程中,点P到点O的距离不发生变化,永远是a.故选B.
6.B 7.C 8.B 9.C 10.A
二、11. 12.
13. 点拨:过点C作CD⊥AB于点D.∵AC=6,sinA=,∴CD=4.在Rt△BCD中,∠BDC=90°,BC=5,CD=4,∴BD=3,∴tanB==.
14.30 15.6
16.3或3 或3 点拨:当∠APB=90°时,分两种情况讨论.情况一:如图①,∵AO=BO,∴PO=BO=AO,∵∠1=120°,∴∠AOP=60°,∴△AOP为等边三角形,∴AP=OA=AB=3;情况二:如图②,∵AO=BO,∠APB=90°,∴PO=BO,∵∠1=120°,∴∠BOP=60°,∴△BOP为等边三角形,∴∠OBP=60°,∴AP=AB·sin60°=6×=3 .当∠BAP=90°时,如图③,∵∠1=120°,∴∠AOP=60°,∴AP=OA·tan∠AOP=3×=3 ;当∠ABP=90°时,如图④,∵∠1=120°,∴∠BOP=60°,∵OB=3,∴PB=3 ,∴PA==3 ,故答案为:3或3 或3 .
三、17.解:(1)原式=×-2×1+=-2+=0.
(2)原式=4×--=4×--2=1--2=-1-.
18.解:作AD⊥BC,交BC的延长线于D,
∵∠BCA=135°,∴∠ACD=45°.
在Rt△ACD中,AC=2,∠ACD=45°,
∴CD=AD=AC·sin45°=2 ×=2.
在Rt△BDA中,BD=BC+CD=6,AD=2.
∴AB==2.
19.解:(1)过A作AE⊥BC于E,
∵∠B=45°,sinB=,
∴AE=AB·sinB=3 ×=3.
∴BE=AE=3.
∵∠AEC=90°,tanC==,
∴CE=15,
∴BC=BE+CE=18.
(2)∵D是BC中点,∴BD=BC=9,∴DE=BD-BE=6.
∴AD==3 .
∴sin∠ADB===.
20.解:过点C作CD⊥AB,交BA的延长线于点D.则AD的长即为潜艇C的下潜深度.
根据题意得∠ACD=30°,∠BCD=68°.
设AD=x 米,则BD=BA+AD=(1 000+x)米,
在Rt△ACD中,CD=x米,
在Rt△BCD中,BD=CD·tan68°,
∴1 000+x=x·tan68°.
将tan68°≈2.5,≈1.7代入解得x≈308,
∴潜艇C离开海平面的下潜深度约为308米.
21.解:(1)如图,作BH⊥AC,垂足为H.在Rt△BHC中,sinC==,即BC=2BH.
在Rt△BHA中,sinA==,即AB=BH.
∴thiA==.
(2)60°或120°
(3)如图,在△ABC中,thiA=.
在Rt△BHA中,sinA=.
在Rt△BHC中,sinC==,即BC=2BH.∴thiA=2sinA.
22.(1)证明:如图,过点A作DC的垂线AM,交DC于点M,则AM=BC=2.
∵tan ∠ADC==2,
∴DM==1.
又∵MC=AB=1,
∴DC=DM+MC=2,∴DC=BC.
(2)解:△ECF是等腰直角三角形.
证明:如图,∵DE=BF,∠EDC=∠FBC,DC=BC,
∴△DEC≌△BFC,
∴∠1=∠3,EC=FC.
∴∠3+∠2=∠1+∠2=90°.
∴△ECF为等腰直角三角形.
(3)解:在(2)的条件下,
∵∠BEC=135°,
∴∠BEF=135°-45°=90°.
∵BE ∶CE=1 ∶2,设BE=k,CE=2k,
∴EF=2 k,∴BF===3k.
在Rt△BEF中,sin ∠BFE===.
一、选择题(每题3分,共30分)
1.在Rt△ABC中,cosA=,那么∠A的度数为( )
A.45° B.60° C.30° D.无法确定
2.在Rt△ABC中,∠C=90°,若AB=3BC,则tanA的值是( )
A. B.3 C.2 D.
3.已知锐角α,且sinα=cos37°,则α等于( )
A.37° B.63° C.53° D.45°
4.如图,在△ABC中,AB=3,BC=2,∠B=60°,则△ABC的面积等于( )
A. B. C. D.3
5.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A.变小 B.不变 C.变大 D.无法判断
6.点M(-sin 60°,cos 60°)关于x轴对称的点的坐标是( )
A. B. C. D.
7.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cos α=,AB=4,则AC的长为( )
A.3 B. C. D.
8.已知45°<∠A<90°,则下列各式成立的是( )
A.sin A=cos A B.sin A>cos A C.sin A>tan A D.sin A
A.8米 B.8 米 C.米 D.米
10.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶端恰好看到矮建筑物的墙脚C,且俯角α为60°,又从A点测得D点的俯角β为30°.若旗杆底部点G为BC的中点,则矮建筑物的高CD为( )
A.20米 B.10 米 C.15 米 D.5 米
二、填空题(每题3分,共18分)
11.求值:sin60°-tan30°=________.
12.已知α是锐角且tanα=,则sinα+cosα=________.
13.在△ABC中,AC=6,BC=5,sinA=,∠B为锐角,则tanB=________.
14.如图,一束光线照在坡度为1∶ 的斜坡上,被斜坡上的平面镜反射成与地面平行的光线,则这束光线与坡面的夹角α是________度.
15.如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中,距灯塔S的最近距离是________海里.
16.如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=________.
三、解答题(17~20题每题8分,21~22题每题10分,共52分)
17.计算下列各题:
(1) cos 30°-2tan 45°+sin 30°;
(2)·cos260°--.
18.如图,在△ABC中,∠BCA=135°,AC=2 ,BC=4,求AB的长.
19.如图,△ABC中,∠B=45°,AB=3 ,D是BC中点,tanC=.求:
(1)BC的长;
(2)sin∠ADB.
20.如图,某次“海上联合”反潜演习中,我军舰A测得潜艇C的俯角为30°.位于军舰A正上方1 000米的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数.参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5, ≈1.7)
21.定义:我们把∠A的对边与∠C 的对边的比叫做∠A的邻弦,记作thi A,即thi A==.请解答下列问题:
已知:在△ABC中,∠C=30°.
(1)若∠A=45°,求thi A的值;
(2)若thi A= ,则∠A=________;
(3)若∠A是锐角,探究thi A与sinA的数量关系.
22.如图,在梯形ABCD中,AB∥DC,∠BCD=90°,且AB=1,BC=2,
tan ∠ADC=2.
(1)求证:DC=BC;
(2)E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
(3)在(2)的条件下,当BE∶CE=1∶2,∠BEC=135°时,求sin ∠BFE.
答案
一、1.B 2.D 3.C
4.A 点拨:过点C作AB的垂线,垂足为D,则CD=BCsinB,△ABC的面积S=AB·BCsinB=×3×2×sin60°= .
5.B 点拨:连结OP,∵∠AOB=90°,P为AB中点,设AB=2a,则OP=AB=a,即在木棍滑动的过程中,点P到点O的距离不发生变化,永远是a.故选B.
6.B 7.C 8.B 9.C 10.A
二、11. 12.
13. 点拨:过点C作CD⊥AB于点D.∵AC=6,sinA=,∴CD=4.在Rt△BCD中,∠BDC=90°,BC=5,CD=4,∴BD=3,∴tanB==.
14.30 15.6
16.3或3 或3 点拨:当∠APB=90°时,分两种情况讨论.情况一:如图①,∵AO=BO,∴PO=BO=AO,∵∠1=120°,∴∠AOP=60°,∴△AOP为等边三角形,∴AP=OA=AB=3;情况二:如图②,∵AO=BO,∠APB=90°,∴PO=BO,∵∠1=120°,∴∠BOP=60°,∴△BOP为等边三角形,∴∠OBP=60°,∴AP=AB·sin60°=6×=3 .当∠BAP=90°时,如图③,∵∠1=120°,∴∠AOP=60°,∴AP=OA·tan∠AOP=3×=3 ;当∠ABP=90°时,如图④,∵∠1=120°,∴∠BOP=60°,∵OB=3,∴PB=3 ,∴PA==3 ,故答案为:3或3 或3 .
三、17.解:(1)原式=×-2×1+=-2+=0.
(2)原式=4×--=4×--2=1--2=-1-.
18.解:作AD⊥BC,交BC的延长线于D,
∵∠BCA=135°,∴∠ACD=45°.
在Rt△ACD中,AC=2,∠ACD=45°,
∴CD=AD=AC·sin45°=2 ×=2.
在Rt△BDA中,BD=BC+CD=6,AD=2.
∴AB==2.
19.解:(1)过A作AE⊥BC于E,
∵∠B=45°,sinB=,
∴AE=AB·sinB=3 ×=3.
∴BE=AE=3.
∵∠AEC=90°,tanC==,
∴CE=15,
∴BC=BE+CE=18.
(2)∵D是BC中点,∴BD=BC=9,∴DE=BD-BE=6.
∴AD==3 .
∴sin∠ADB===.
20.解:过点C作CD⊥AB,交BA的延长线于点D.则AD的长即为潜艇C的下潜深度.
根据题意得∠ACD=30°,∠BCD=68°.
设AD=x 米,则BD=BA+AD=(1 000+x)米,
在Rt△ACD中,CD=x米,
在Rt△BCD中,BD=CD·tan68°,
∴1 000+x=x·tan68°.
将tan68°≈2.5,≈1.7代入解得x≈308,
∴潜艇C离开海平面的下潜深度约为308米.
21.解:(1)如图,作BH⊥AC,垂足为H.在Rt△BHC中,sinC==,即BC=2BH.
在Rt△BHA中,sinA==,即AB=BH.
∴thiA==.
(2)60°或120°
(3)如图,在△ABC中,thiA=.
在Rt△BHA中,sinA=.
在Rt△BHC中,sinC==,即BC=2BH.∴thiA=2sinA.
22.(1)证明:如图,过点A作DC的垂线AM,交DC于点M,则AM=BC=2.
∵tan ∠ADC==2,
∴DM==1.
又∵MC=AB=1,
∴DC=DM+MC=2,∴DC=BC.
(2)解:△ECF是等腰直角三角形.
证明:如图,∵DE=BF,∠EDC=∠FBC,DC=BC,
∴△DEC≌△BFC,
∴∠1=∠3,EC=FC.
∴∠3+∠2=∠1+∠2=90°.
∴△ECF为等腰直角三角形.
(3)解:在(2)的条件下,
∵∠BEC=135°,
∴∠BEF=135°-45°=90°.
∵BE ∶CE=1 ∶2,设BE=k,CE=2k,
∴EF=2 k,∴BF===3k.
在Rt△BEF中,sin ∠BFE===.
