2020年秋人教版八年级数学上册11.3多边形及其内角和同步练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版八年级数学上册11.3多边形及其内角和同步练习(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 127.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-08 00:00:00 | ||
图片预览

文档简介
11.3多边形及其内角和
一、选择题
1.
若在n边形内部任意取一点P,将点P与各顶点连接起来,可以把n边形分成n个三角形,利用这个事实,可以探索到n边形的内角和为( )
A.180°×n
B.180°×n-180°
C.180°×n+180°
D.180°×n-360°
2.
如图所示,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2的度数为(
)
A.135°
B.240°
C.270°
D.300°
3.四边形ABCD中,∠A+∠C=∠B+∠D,∠A的外角为120°,则∠C的度数为( )
A.36°
????
B.60°???
?
C.90°??
??
D.120°
4.从n边形的一个顶点出发共有对角线(
)
A.(n-2)条
B.(n-3)条
C.(n-1)条
D.(n-4)条
5.如果一个正多边形的中心角是60°,那么这个正多边形的边数是( )
A.4???????
B.5???????
C.6????
D.7
6.
下列哪一个度数可以作为某一个多边形的内角和
( )
A.240°
B.600°
C.540°
D.2180°
7.四边形的内角和等于(
)
A.180°
B.270°
C.360°
D.150°
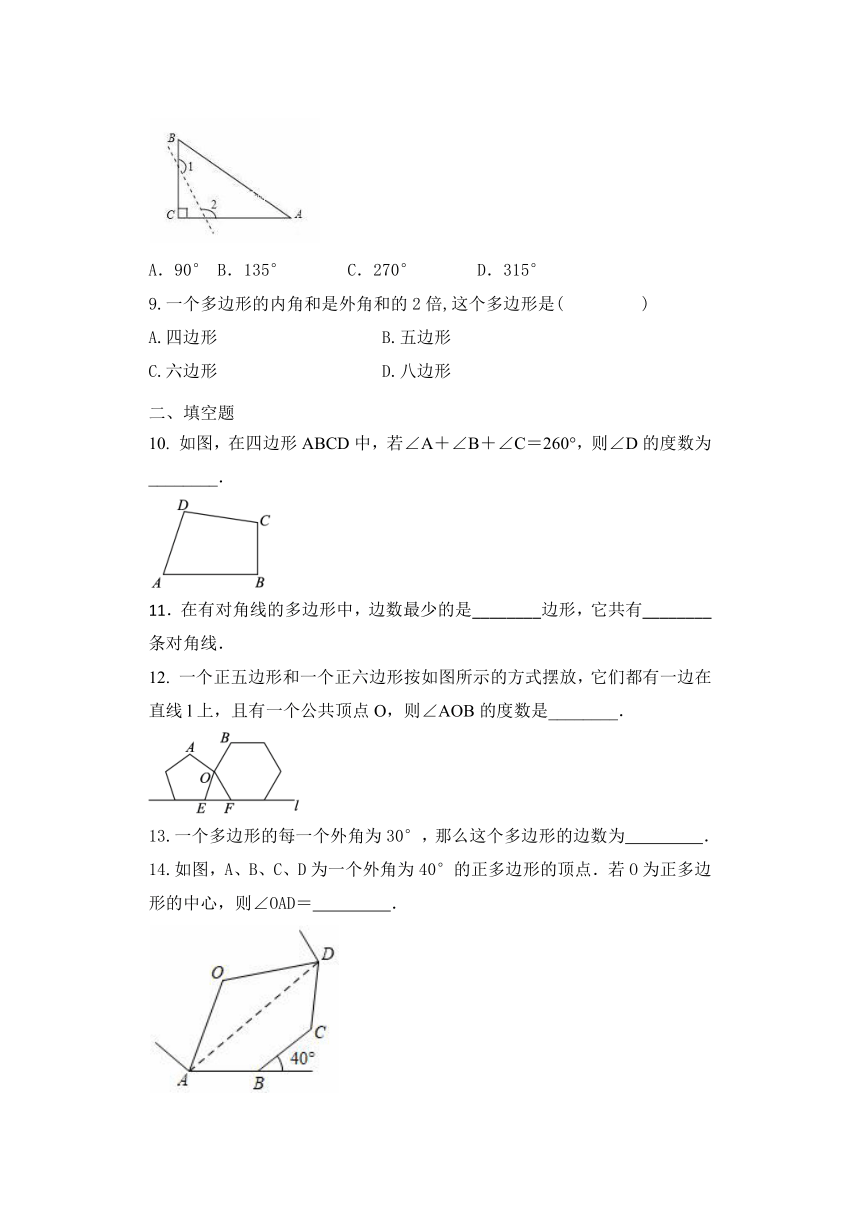
8.如图,已知△ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
?
A.90°
B.135°???
C.270°???
D.315°
9.一个多边形的内角和是外角和的2倍,这个多边形是(????
)
A.四边形?????????
B.五边形
C.六边形?????????
D.八边形
二、填空题
10.
如图,在四边形ABCD中,若∠A+∠B+∠C=260°,则∠D的度数为________.
11.在有对角线的多边形中,边数最少的是________边形,它共有________条对角线.
12.
一个正五边形和一个正六边形按如图所示的方式摆放,它们都有一边在直线l上,且有一个公共顶点O,则∠AOB的度数是________.
13.一个多边形的每一个外角为30°,那么这个多边形的边数为 ??
.
14.如图,A、B、C、D为一个外角为40°的正多边形的顶点.若O为正多边形的中心,则∠OAD= ??
.
三、解答题
15.已知多边形的边数恰好是从这个多边形的一个顶点出发的对角线条数的2倍,求此多边形的边数.
16.
“X”与“Y”分别是两个多边形,请根据图中“X”与“Y”的对话,解答下列各小题.
(1)求“X”与“Y”的外角和相加的度数;
(2)分别求“X”与“Y”的内角和的度数.
17.一个多边形的内角和与外角和的和是,通过计算说明它是几边形.
18.(1)如图①所示,∠1+∠2与∠B+∠C有什么关系?为什么?
(2)如图②若把△ABC纸片沿DE点折叠当点A落在四边形BCED内部时,则∠A与∠α+∠β之间有一种数量关系始终保持不变,请写出这个规律并说明理由.
答案
1.
D
2.
C
3.
D
4.
B
5.
C
6.
C
7.
C
8.
C
9.
C
10.
100°
11.
四,
2
12.
84°
13.
12.
14.
140°
15.
设多边形的边数为n,根据题意,有:
n=2(n-3),
解得n=6,
故这个多边形的边数为6.
16.
(1)360°+360°=720°.
(2)设X的边数为n,则Y的边数为3n.
由题意,得180(n-2)+180(3n-2)=1440,
解得n=3.
所以X的内角和为180°×(3-2)=180°,
Y的内角和为180°×(3×3-2)=1260°.
答:“X”的内角和的度数为180°,“Y”的内角和的度数为1260°.
17.
n=8,?
18.
解:(1)∠1+∠2=∠B+∠C,
∵如图1,在△AED和△ACB中,
∠1+∠2+∠A=∠A+∠B+∠C=180°(三角形内角和等于180°),
∴∠1+∠2=∠B+∠C(等量代换).
(2)规律:α+β=2∠A.
理由:∵在△ADE中,∠1+∠2=180°﹣∠A(三角形内角和等于180°),
在四边形BCED中,∠BDE+∠DEC+∠B+∠C=360°(四边形内角和等于360°),
又∵根据题(1)得∠1+∠2=∠B+∠C(已证),
∴2(∠1+∠2)+α+β=360°(等量代换),
∴2(180°﹣∠A)+α+β=360°(等量代换),
∴α+β=2∠A.
一、选择题
1.
若在n边形内部任意取一点P,将点P与各顶点连接起来,可以把n边形分成n个三角形,利用这个事实,可以探索到n边形的内角和为( )
A.180°×n
B.180°×n-180°
C.180°×n+180°
D.180°×n-360°
2.
如图所示,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2的度数为(
)
A.135°
B.240°
C.270°
D.300°
3.四边形ABCD中,∠A+∠C=∠B+∠D,∠A的外角为120°,则∠C的度数为( )
A.36°
????
B.60°???
?
C.90°??
??
D.120°
4.从n边形的一个顶点出发共有对角线(
)
A.(n-2)条
B.(n-3)条
C.(n-1)条
D.(n-4)条
5.如果一个正多边形的中心角是60°,那么这个正多边形的边数是( )
A.4???????
B.5???????
C.6????
D.7
6.
下列哪一个度数可以作为某一个多边形的内角和
( )
A.240°
B.600°
C.540°
D.2180°
7.四边形的内角和等于(
)
A.180°
B.270°
C.360°
D.150°
8.如图,已知△ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
?
A.90°
B.135°???
C.270°???
D.315°
9.一个多边形的内角和是外角和的2倍,这个多边形是(????
)
A.四边形?????????
B.五边形
C.六边形?????????
D.八边形
二、填空题
10.
如图,在四边形ABCD中,若∠A+∠B+∠C=260°,则∠D的度数为________.
11.在有对角线的多边形中,边数最少的是________边形,它共有________条对角线.
12.
一个正五边形和一个正六边形按如图所示的方式摆放,它们都有一边在直线l上,且有一个公共顶点O,则∠AOB的度数是________.
13.一个多边形的每一个外角为30°,那么这个多边形的边数为 ??
.
14.如图,A、B、C、D为一个外角为40°的正多边形的顶点.若O为正多边形的中心,则∠OAD= ??
.
三、解答题
15.已知多边形的边数恰好是从这个多边形的一个顶点出发的对角线条数的2倍,求此多边形的边数.
16.
“X”与“Y”分别是两个多边形,请根据图中“X”与“Y”的对话,解答下列各小题.
(1)求“X”与“Y”的外角和相加的度数;
(2)分别求“X”与“Y”的内角和的度数.
17.一个多边形的内角和与外角和的和是,通过计算说明它是几边形.
18.(1)如图①所示,∠1+∠2与∠B+∠C有什么关系?为什么?
(2)如图②若把△ABC纸片沿DE点折叠当点A落在四边形BCED内部时,则∠A与∠α+∠β之间有一种数量关系始终保持不变,请写出这个规律并说明理由.
答案
1.
D
2.
C
3.
D
4.
B
5.
C
6.
C
7.
C
8.
C
9.
C
10.
100°
11.
四,
2
12.
84°
13.
12.
14.
140°
15.
设多边形的边数为n,根据题意,有:
n=2(n-3),
解得n=6,
故这个多边形的边数为6.
16.
(1)360°+360°=720°.
(2)设X的边数为n,则Y的边数为3n.
由题意,得180(n-2)+180(3n-2)=1440,
解得n=3.
所以X的内角和为180°×(3-2)=180°,
Y的内角和为180°×(3×3-2)=1260°.
答:“X”的内角和的度数为180°,“Y”的内角和的度数为1260°.
17.
n=8,?
18.
解:(1)∠1+∠2=∠B+∠C,
∵如图1,在△AED和△ACB中,
∠1+∠2+∠A=∠A+∠B+∠C=180°(三角形内角和等于180°),
∴∠1+∠2=∠B+∠C(等量代换).
(2)规律:α+β=2∠A.
理由:∵在△ADE中,∠1+∠2=180°﹣∠A(三角形内角和等于180°),
在四边形BCED中,∠BDE+∠DEC+∠B+∠C=360°(四边形内角和等于360°),
又∵根据题(1)得∠1+∠2=∠B+∠C(已证),
∴2(∠1+∠2)+α+β=360°(等量代换),
∴2(180°﹣∠A)+α+β=360°(等量代换),
∴α+β=2∠A.
