4.4.2一次函数的应用(2)(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 4.4.2一次函数的应用(2)(知识清单+经典例题+夯实基础+提优特训+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 732.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 09:53:35 | ||
图片预览


文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学上册第四章一次函数
4.4
一次函数的应用
第2课时
一次函数的应用(2)
【知识清单】
一次函数与一元一次方程的关系:
1、从形上看:一次函数的一般形式为:y=kx+b,一元一次方程的一般形式可化为kx+b=0;
2、从函数值角度看:当一次函数y=kx+b函数值为0时,相应的自变量的值就是方程
kx+b=0的解;
3、从图象上看:一次函数y=kx+b的图象与x轴的交点的横坐标就是方程kx+b=0的解;
【经典例题】
【例题】1、已知关于x的方程ax+b=0的解是x=5,则直线y=ax+b与x轴的交点坐标是____.
【考点】一次函数与一元一次方程.
【分析】求直线与x轴的交点坐标,需使直线y=ax+b的y值为0,则ax+b=0;已知此方程的解为x=5.因此可得答案.
【解答】∵方程的解为x=5,
∴当x=5时ax+b=0;
又∵直线y=ax+b与x轴的交点的纵坐标是0,
∴当y=0时,则有ax+b=0,
∴x=5时,y=0.
∴直线y=ax+b与x轴的交点坐标是(5,0).
【点评】本题主要考查了一次函数与一元一次方程的关系.任何一元一次方程都可以转化为ax+b=0
(a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值.从图象上看,相当于已知直线y=ax+b确定它与x轴的交点的横坐标的值.
【例题】2、在空中,自地面算起,每升高1km,气温下降若干度(°C),某地空中气温t°C与高度h(km)间的函数图象如图所示,观察图象可知,地面气温为
°C.当高度为???
km时,气温为0°C.
(1)求t与h的函数解析式;(2)若该市空中气温为15°C,则此处离地面有多高?
【考点】函数的图象的应用.
【分析】根据图象的横坐标和纵坐标所表示的意义解答.
【解答】由图象知:横坐标表示某地高度h(km)、纵坐标表示某地空中气温t°C,
当高度为0(即地面)时,所对应的某地空中气温是24°C,
故答案为24°C.当高度为6km时,气温为0°C.
解:
(1)由题知设t=kh+b
由图像过点(0,24),(6,0)
知k×0+b=24,k×6+b=0,
解得k=4,b=24
即t与h的函数解析式t=244h;
(2)由t=15,即244h=15,
解得h=,
故该市空中气温为15°C,则此处离地面有千米.
【点评】正确理解函数图象横纵坐标表示的意义,理解问题的过程,能够通过图象得到函数与自变量的对应关系是解题的关键.
【夯实基础】
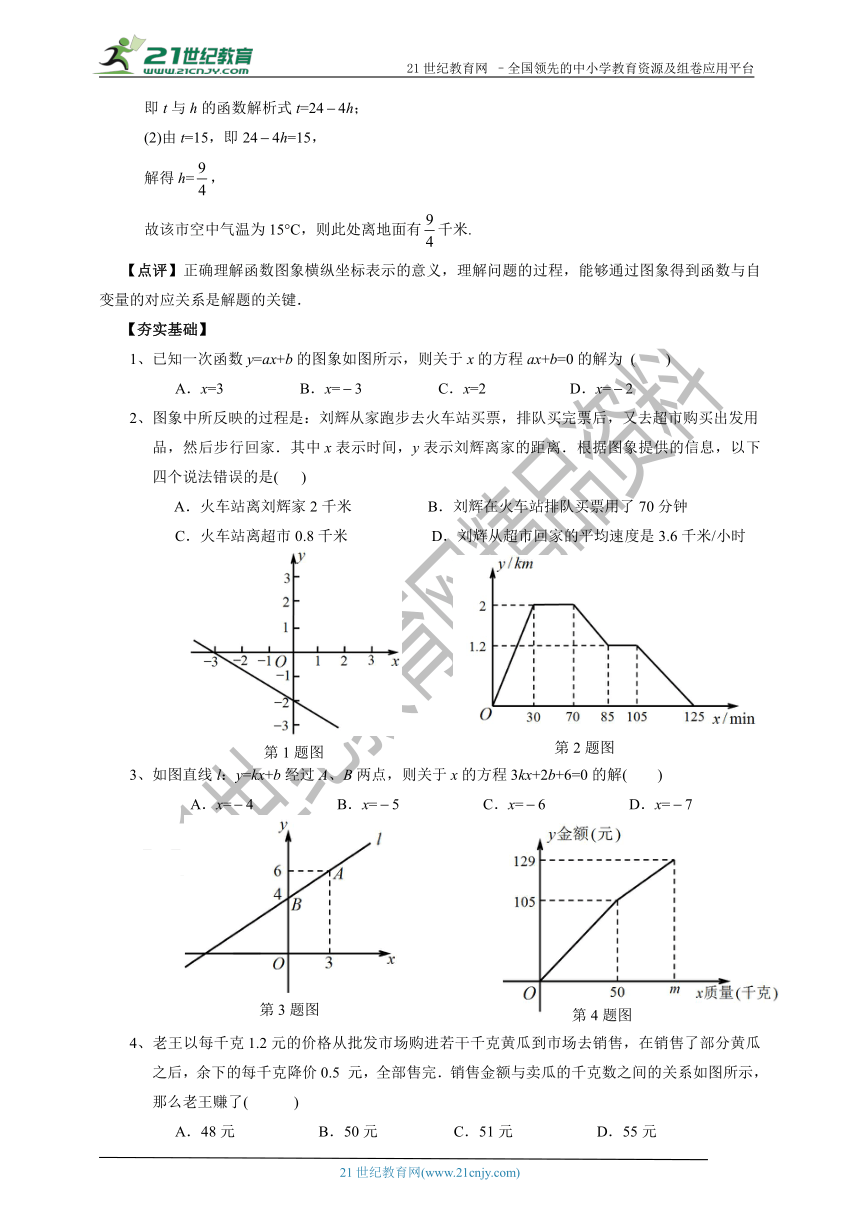
1、已知一次函数y=ax+b的图象如图所示,则关于x的方程ax+b=0的解为
( )
A.x=3
B.x=3
C.x=2
D.x=2
2、图象中所反映的过程是:刘辉从家跑步去火车站买票,排队买完票后,又去超市购买出发用
品,然后步行回家.其中x表示时间,y表示刘辉离家的距离.根据图象提供的信息,以下四个说法错误的是(
)
A.火车站离刘辉家2千米
B.刘辉在火车站排队买票用了70分钟
C.火车站离超市0.8千米
D.刘辉从超市回家的平均速度是3.6千米/小时
3、如图直线l:y=kx+b经过A、B两点,则关于x的方程3kx+2b+6=0的解(
)
A.x=4
B.x=5
C.x=6
D.x=7
4、老王以每千克1.2元的价格从批发市场购进若干千克黄瓜到市场去销售,在销售了部分黄瓜之后,余下的每千克降价0.5
元,全部售完.销售金额与卖瓜的千克数之间的关系如图所示,那么老王赚了(
)
A.48元
B.50元
C.51元
D.55元
5、直线y=5x10与x轴的交点的横坐标x的值是方程3x2a=12的解,则a值为
.
6、已知一次函数y=mx+5和y=xn的图像都经过点A(5,2),则关于x的方程mx+5=xn
的解是
.
7、(1)方程5x4=6的解是
,则函数y=5x4在自变量x等于
时的函数值是6.
(2)
在糖水中继续放入糖x(g)、水y(g),并使糖完全溶解,如果甜度保持不变,那么y与x的函数关系一定是
.
8、一盘蚊香长105cm,点燃后每小时缩短10cm.(1)请写出点燃后蚊香的长y(cm)与蚊香
燃烧时间t(h)之间的函数关系式;(2)该蚊香可点燃多长时间?
9、李峰同学骑自行车到学校上学,学校离家16千米,他离家的距离s(千米)和时间t(分
钟)的关系如图所示.根据图象回答下列问题:
(1)李峰从家到学校用多少时间?
(2)李峰15分钟骑自行车行驶多少路程?
(3)李峰骑车行驶10千米,需多少时间?
(4)
李峰骑车的速度是多少?
【提优特训】
10、如图是一同学骑自行车出行的图象,从图象中得到的正确的信息是(
)
A.整个出行过程中的平均速度为5千米/小时
B.前30分钟的速度比后1小时的速度慢
C.前30分钟的速度比后1小时的速度快
D.从起点到达终点,该同学共用了1小时分钟
11、甲、乙两辆电动自行车同时从相距24km的A,B两地出发,相向而行.图中l1,l2分别表示
甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系.则下列说法错误的是( )
A.经过0.
5小时两电动自行车相遇
B.经过0.6小时甲电动自行车行驶到A,B两地的中点
C.乙电动自行车的速度每小时比甲自行车的速度快4km
D.当乙摩托车到达A地时,甲摩托车距离A地20km
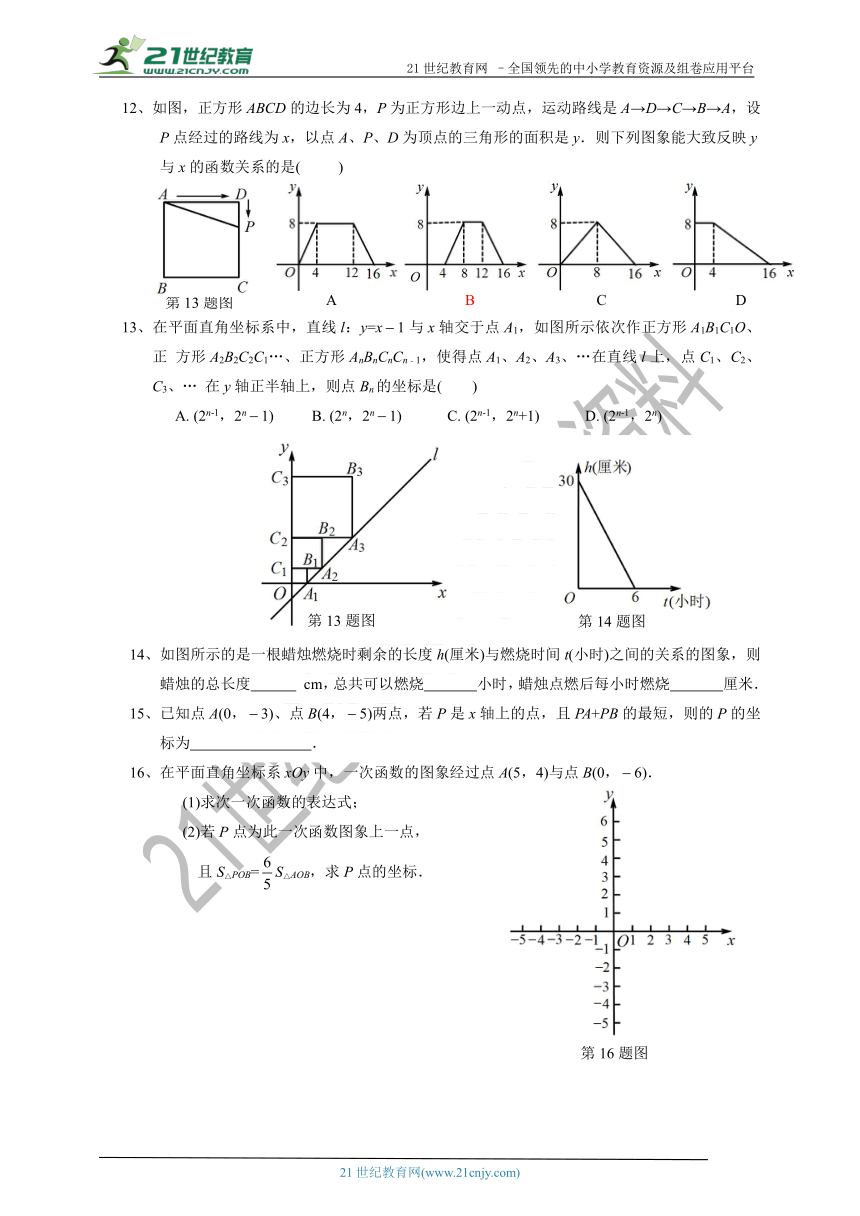
12、如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路线为x,以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是(
)
13、在平面直角坐标系中,直线l:y=x1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正
方形A2B2C2C1…、正方形AnBnCnCn﹣1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…
在y轴正半轴上,则点Bn的坐标是( )
A.?(2n-1,2n1)???
?B.?(2n,2n1)???
?C.?(2n-1,2n+1)
????D.?(2n-1,2n)
14、如图所示的是一根蜡烛燃烧时剩余的长度h(厘米)与燃烧时间t(小时)之间的关系的图象,则蜡烛的总长度
cm,总共可以燃烧
小时,蜡烛点燃后每小时燃烧
厘米.
15、已知点A(0,3)、点B(4,5)两点,若P是x轴上的点,且PA+PB的最短,则的P的坐标为
.
16、在平面直角坐标系xOy中,一次函数的图象经过点A(5,4)与点B(0,6).
(1)求次一次函数的表达式;
(2)若P点为此一次函数图象上一点,
且S△POB=S△AOB,求P点的坐标.
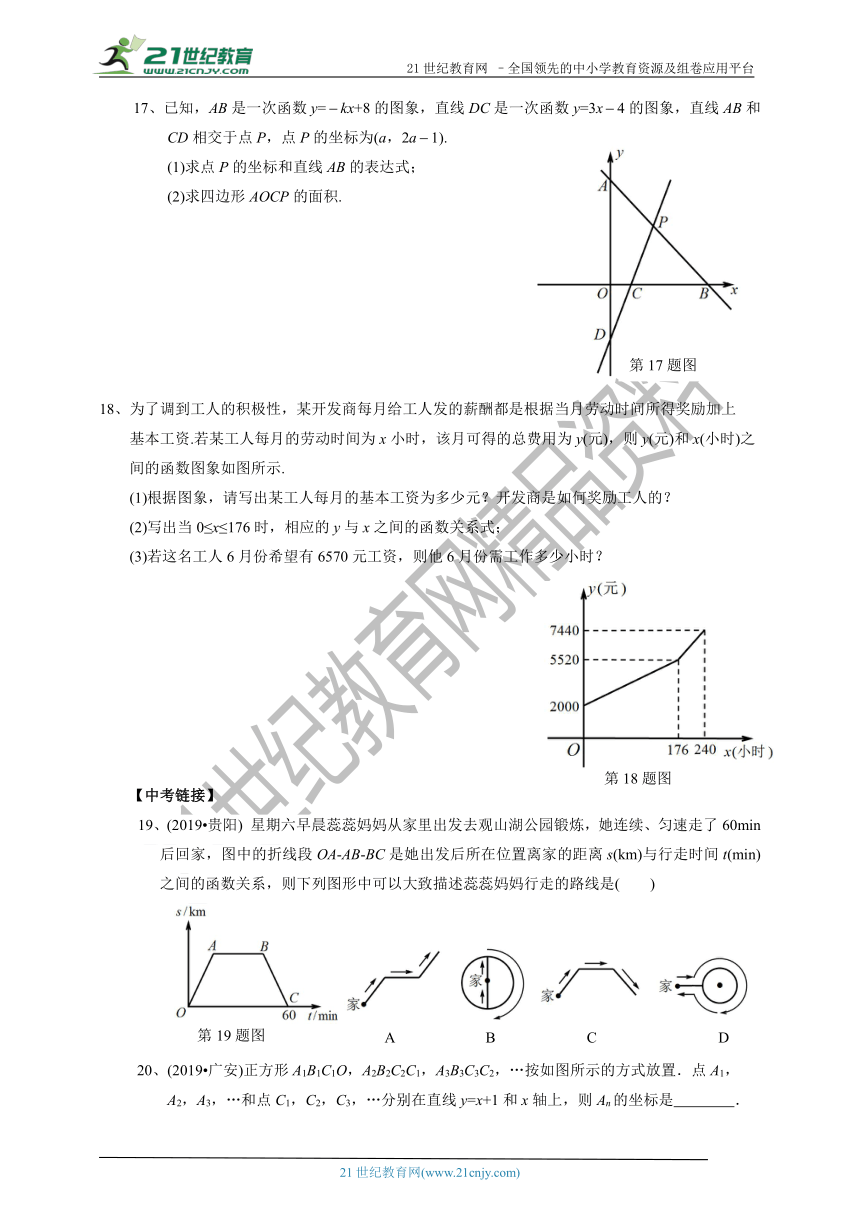
?17、已知,AB是一次函数y=kx+8的图象,直线DC是一次函数y=3x4的图象,直线AB和CD相交于点P,点P的坐标为(a,2a1).
(1)求点P的坐标和直线AB的表达式;
(2)求四边形AOCP的面积.
18、为了调到工人的积极性,某开发商每月给工人发的薪酬都是根据当月劳动时间所得奖励加上
基本工资.若某工人每月的劳动时间为x小时,该月可得的总费用为y(元),则y(元)和
x(小时)之间的函数图象如图所示.?
(1)根据图象,请写出某工人每月的基本工资为多少元?开发商是如何奖励工人的?
(2)写出当0≤x≤176时,相应的y与x之间的函数关系式;
(3)若这名工人6月份希望有6570元工资,
则他6月份需工作多少小时?
【中考链接】
19、(2019?贵阳)
星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA-AB-BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
20、(2019?广安)正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,
A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则An的坐标是
.
21、(2019?嘉兴)如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(2,0),
(1,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标是
.
22、(2019?泰安)在平面直角坐标系中,
直线l:y=x+1与x轴交于点A1,
如图所示,依次作正方形OA1B1C1、
正方形C1A2B2C2正方形C2A3B3C3,
正方形C3A4B4C4、…,点A1、A2、
A3、…在直线l上,点C1、C2、
C3、…在x轴正半轴上,则前n个
正方形对角线的和为
.
参考答案
1、B
2、B
3、D
4、C
5、3
6、x=5
7、(1)
x=2,x=2
(2)正比例函数
10、C
11、A
12、B
13、A
14、30,
6,5
15、
19、B
20、(2n-11,2n-1)
21、(1,3)
22、
8、一盘蚊香长105cm,点燃后每小时缩短10cm.(1)请写出点燃后蚊香的长y(cm)与蚊香
燃烧时间t(h)之间的函数关系式;(2)该蚊香可点燃多长时间?
解:t=10.5,(1)∵点燃后蚊香的长等于蚊香的原长减去燃烧的长度,
∴y=10510t(0≤t≤10.5);
(2)∵蚊香燃尽的时候蚊香的长度y=0,
∴10510t=0,
解得:t=10.5,
∴该蚊香可点燃10.5小时.
9、李峰同学骑自行车到学校上学,学校离家16千米,他离家的距离s(千米)和时间t(分
钟)的关系如图所示.根据图象回答下列问题:
(1)李峰从家到学校用多少时间?
(2)李峰15分钟骑自行车行驶多少路程?
(3)李峰骑车行驶10千米,需多少时间?
(4)
李峰骑车的速度是多少?
解:设s与t的函数关系式为:s=kt,
将t=25,s=8代入s=kt得,8=25k
解得k=,∴s与t的函数关系式为:s=t,
(1)李峰从家到学校用50分钟;
(2)当t=15时,骑自行车行驶路程为:(千米);
(3)当s=10时,则10=t,解得t=(分钟);
(4)16÷=19.2(千米/小时).
16、在平面直角坐标系xOy中,一次函数的图象经过点A(5,4)与点B(0,6).
(1)求次一次函数的表达式;
(2)若P点为此一次函数图象上一点,且S△POB=S△AOB,求P点的坐标.
解:(1)设一次函数的解析式为y=kx+b,
将A(5,4)、B(0,6)代入得:5k+b=4,b=6,
解得:k=2,b=6,
∴一次函数表达式为y=2x6;
(2)设P(a,2a6),PE=,
∵S△POB=S△AOB,
∴?OB?PE=?OB?AD,即×6×=××6×5,
解得:a=6或a=6,
∴点P的坐标为(6,6)或(6,18).
?17、已知,AB是一次函数y=kx+8的图象,直线DC是一次函数y=3x4的图象,直线AB和CD相交于点P,点P的坐标为(a,2a1).
(1)求点P的坐标和直线AB的表达式;
(2)求四边形AOCP的面积.
解:(1)∵点P(a,2a1)在直线y=3x4上,
∴2a1=3a4,
解得a=3,2a1=5,
∴点P的坐标为(3,5),
将点P(3,5)代入y=kx+8得,
5=3k+8,
解得k=1,
∴直线AB的表达式为:y=x+8;
(2)在一次函数y=3x4中,令x=0,y=4,令x=,y=0,
∴点C的坐标为(,0),
在一次函数y=x+8中,令x=0,y=8,
∴点A的坐标为(0,8),
∴AD=8(4)=18,点P到y轴的距离为3,
四边形AOCP的面积=S△ADPS△DOC
=×3ADOD·OC
=×3×12××4=.
18、为了调到工人的积极性,某开发商每月给工人发的薪酬都是根据当月劳动时间所得奖励加上
基本工资.若某工人每月的劳动时间为x小时,该月可得的总费用为y(元),则y(元)和
x(小时)之间的函数图象如图所示.?
(1)根据图象,请写出某工人每月的基本工资为多少元?开发商是如何奖励工人的?
(2)写出当0≤x≤176时,相应的y与x之间的函数关系式;
(3)若这名工人6月份希望有6570元工资,
则他6月份需工作多少小时?
解:(1)∵x=0时,y=2000,
∴这名工人每月的基本工资为2000元;
如果这名每月工作时间不超过176小时,
每小时获奖励20元;如果这名每月
劳动时间超过176小时,每小时30元奖励.
(2)设当0≤x≤176时,相应的y与x之间的函数关系式为y=kx+2000,
将x=176,y=5520代入y=kx+2000,得5520=176k+2000,
解得k=20,
y与x之间的函数关系式为y=20x+2000;
(3)∵74405520=1920,1920÷(240176)=30,
当x≥176时,设y与x的函数关系式为:y=30x+b.
将x=176,y=5520代入y=30x+b,得5520=30×176+b,
解得b=240,
∴当x≥176时,设y与x的函数关系式为:y=30x+240.
当y=6570时,
由题意得,30x+240=6570
解得
x=211小时,
答:他6月份需工作211小时.
第18题图
第11题图
第2题图
第9题图
第14题图
第2题图
第22题图
第3题图
第20题图
第18题图
第13题图
第4题图
第1题图
第9题图
第13题图
A
B
C
D
第17题图
第19题图
第16题图
第17题图
第10题图
第16题图
第21题图
第16题图
A
B
C
D
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学上册第四章一次函数
4.4
一次函数的应用
第2课时
一次函数的应用(2)
【知识清单】
一次函数与一元一次方程的关系:
1、从形上看:一次函数的一般形式为:y=kx+b,一元一次方程的一般形式可化为kx+b=0;
2、从函数值角度看:当一次函数y=kx+b函数值为0时,相应的自变量的值就是方程
kx+b=0的解;
3、从图象上看:一次函数y=kx+b的图象与x轴的交点的横坐标就是方程kx+b=0的解;
【经典例题】
【例题】1、已知关于x的方程ax+b=0的解是x=5,则直线y=ax+b与x轴的交点坐标是____.
【考点】一次函数与一元一次方程.
【分析】求直线与x轴的交点坐标,需使直线y=ax+b的y值为0,则ax+b=0;已知此方程的解为x=5.因此可得答案.
【解答】∵方程的解为x=5,
∴当x=5时ax+b=0;
又∵直线y=ax+b与x轴的交点的纵坐标是0,
∴当y=0时,则有ax+b=0,
∴x=5时,y=0.
∴直线y=ax+b与x轴的交点坐标是(5,0).
【点评】本题主要考查了一次函数与一元一次方程的关系.任何一元一次方程都可以转化为ax+b=0
(a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值.从图象上看,相当于已知直线y=ax+b确定它与x轴的交点的横坐标的值.
【例题】2、在空中,自地面算起,每升高1km,气温下降若干度(°C),某地空中气温t°C与高度h(km)间的函数图象如图所示,观察图象可知,地面气温为
°C.当高度为???
km时,气温为0°C.
(1)求t与h的函数解析式;(2)若该市空中气温为15°C,则此处离地面有多高?
【考点】函数的图象的应用.
【分析】根据图象的横坐标和纵坐标所表示的意义解答.
【解答】由图象知:横坐标表示某地高度h(km)、纵坐标表示某地空中气温t°C,
当高度为0(即地面)时,所对应的某地空中气温是24°C,
故答案为24°C.当高度为6km时,气温为0°C.
解:
(1)由题知设t=kh+b
由图像过点(0,24),(6,0)
知k×0+b=24,k×6+b=0,
解得k=4,b=24
即t与h的函数解析式t=244h;
(2)由t=15,即244h=15,
解得h=,
故该市空中气温为15°C,则此处离地面有千米.
【点评】正确理解函数图象横纵坐标表示的意义,理解问题的过程,能够通过图象得到函数与自变量的对应关系是解题的关键.
【夯实基础】
1、已知一次函数y=ax+b的图象如图所示,则关于x的方程ax+b=0的解为
( )
A.x=3
B.x=3
C.x=2
D.x=2
2、图象中所反映的过程是:刘辉从家跑步去火车站买票,排队买完票后,又去超市购买出发用
品,然后步行回家.其中x表示时间,y表示刘辉离家的距离.根据图象提供的信息,以下四个说法错误的是(
)
A.火车站离刘辉家2千米
B.刘辉在火车站排队买票用了70分钟
C.火车站离超市0.8千米
D.刘辉从超市回家的平均速度是3.6千米/小时
3、如图直线l:y=kx+b经过A、B两点,则关于x的方程3kx+2b+6=0的解(
)
A.x=4
B.x=5
C.x=6
D.x=7
4、老王以每千克1.2元的价格从批发市场购进若干千克黄瓜到市场去销售,在销售了部分黄瓜之后,余下的每千克降价0.5
元,全部售完.销售金额与卖瓜的千克数之间的关系如图所示,那么老王赚了(
)
A.48元
B.50元
C.51元
D.55元
5、直线y=5x10与x轴的交点的横坐标x的值是方程3x2a=12的解,则a值为
.
6、已知一次函数y=mx+5和y=xn的图像都经过点A(5,2),则关于x的方程mx+5=xn
的解是
.
7、(1)方程5x4=6的解是
,则函数y=5x4在自变量x等于
时的函数值是6.
(2)
在糖水中继续放入糖x(g)、水y(g),并使糖完全溶解,如果甜度保持不变,那么y与x的函数关系一定是
.
8、一盘蚊香长105cm,点燃后每小时缩短10cm.(1)请写出点燃后蚊香的长y(cm)与蚊香
燃烧时间t(h)之间的函数关系式;(2)该蚊香可点燃多长时间?
9、李峰同学骑自行车到学校上学,学校离家16千米,他离家的距离s(千米)和时间t(分
钟)的关系如图所示.根据图象回答下列问题:
(1)李峰从家到学校用多少时间?
(2)李峰15分钟骑自行车行驶多少路程?
(3)李峰骑车行驶10千米,需多少时间?
(4)
李峰骑车的速度是多少?
【提优特训】
10、如图是一同学骑自行车出行的图象,从图象中得到的正确的信息是(
)
A.整个出行过程中的平均速度为5千米/小时
B.前30分钟的速度比后1小时的速度慢
C.前30分钟的速度比后1小时的速度快
D.从起点到达终点,该同学共用了1小时分钟
11、甲、乙两辆电动自行车同时从相距24km的A,B两地出发,相向而行.图中l1,l2分别表示
甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系.则下列说法错误的是( )
A.经过0.
5小时两电动自行车相遇
B.经过0.6小时甲电动自行车行驶到A,B两地的中点
C.乙电动自行车的速度每小时比甲自行车的速度快4km
D.当乙摩托车到达A地时,甲摩托车距离A地20km
12、如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路线为x,以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是(
)
13、在平面直角坐标系中,直线l:y=x1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正
方形A2B2C2C1…、正方形AnBnCnCn﹣1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…
在y轴正半轴上,则点Bn的坐标是( )
A.?(2n-1,2n1)???
?B.?(2n,2n1)???
?C.?(2n-1,2n+1)
????D.?(2n-1,2n)
14、如图所示的是一根蜡烛燃烧时剩余的长度h(厘米)与燃烧时间t(小时)之间的关系的图象,则蜡烛的总长度
cm,总共可以燃烧
小时,蜡烛点燃后每小时燃烧
厘米.
15、已知点A(0,3)、点B(4,5)两点,若P是x轴上的点,且PA+PB的最短,则的P的坐标为
.
16、在平面直角坐标系xOy中,一次函数的图象经过点A(5,4)与点B(0,6).
(1)求次一次函数的表达式;
(2)若P点为此一次函数图象上一点,
且S△POB=S△AOB,求P点的坐标.
?17、已知,AB是一次函数y=kx+8的图象,直线DC是一次函数y=3x4的图象,直线AB和CD相交于点P,点P的坐标为(a,2a1).
(1)求点P的坐标和直线AB的表达式;
(2)求四边形AOCP的面积.
18、为了调到工人的积极性,某开发商每月给工人发的薪酬都是根据当月劳动时间所得奖励加上
基本工资.若某工人每月的劳动时间为x小时,该月可得的总费用为y(元),则y(元)和
x(小时)之间的函数图象如图所示.?
(1)根据图象,请写出某工人每月的基本工资为多少元?开发商是如何奖励工人的?
(2)写出当0≤x≤176时,相应的y与x之间的函数关系式;
(3)若这名工人6月份希望有6570元工资,
则他6月份需工作多少小时?
【中考链接】
19、(2019?贵阳)
星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA-AB-BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
20、(2019?广安)正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,
A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则An的坐标是
.
21、(2019?嘉兴)如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(2,0),
(1,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标是
.
22、(2019?泰安)在平面直角坐标系中,
直线l:y=x+1与x轴交于点A1,
如图所示,依次作正方形OA1B1C1、
正方形C1A2B2C2正方形C2A3B3C3,
正方形C3A4B4C4、…,点A1、A2、
A3、…在直线l上,点C1、C2、
C3、…在x轴正半轴上,则前n个
正方形对角线的和为
.
参考答案
1、B
2、B
3、D
4、C
5、3
6、x=5
7、(1)
x=2,x=2
(2)正比例函数
10、C
11、A
12、B
13、A
14、30,
6,5
15、
19、B
20、(2n-11,2n-1)
21、(1,3)
22、
8、一盘蚊香长105cm,点燃后每小时缩短10cm.(1)请写出点燃后蚊香的长y(cm)与蚊香
燃烧时间t(h)之间的函数关系式;(2)该蚊香可点燃多长时间?
解:t=10.5,(1)∵点燃后蚊香的长等于蚊香的原长减去燃烧的长度,
∴y=10510t(0≤t≤10.5);
(2)∵蚊香燃尽的时候蚊香的长度y=0,
∴10510t=0,
解得:t=10.5,
∴该蚊香可点燃10.5小时.
9、李峰同学骑自行车到学校上学,学校离家16千米,他离家的距离s(千米)和时间t(分
钟)的关系如图所示.根据图象回答下列问题:
(1)李峰从家到学校用多少时间?
(2)李峰15分钟骑自行车行驶多少路程?
(3)李峰骑车行驶10千米,需多少时间?
(4)
李峰骑车的速度是多少?
解:设s与t的函数关系式为:s=kt,
将t=25,s=8代入s=kt得,8=25k
解得k=,∴s与t的函数关系式为:s=t,
(1)李峰从家到学校用50分钟;
(2)当t=15时,骑自行车行驶路程为:(千米);
(3)当s=10时,则10=t,解得t=(分钟);
(4)16÷=19.2(千米/小时).
16、在平面直角坐标系xOy中,一次函数的图象经过点A(5,4)与点B(0,6).
(1)求次一次函数的表达式;
(2)若P点为此一次函数图象上一点,且S△POB=S△AOB,求P点的坐标.
解:(1)设一次函数的解析式为y=kx+b,
将A(5,4)、B(0,6)代入得:5k+b=4,b=6,
解得:k=2,b=6,
∴一次函数表达式为y=2x6;
(2)设P(a,2a6),PE=,
∵S△POB=S△AOB,
∴?OB?PE=?OB?AD,即×6×=××6×5,
解得:a=6或a=6,
∴点P的坐标为(6,6)或(6,18).
?17、已知,AB是一次函数y=kx+8的图象,直线DC是一次函数y=3x4的图象,直线AB和CD相交于点P,点P的坐标为(a,2a1).
(1)求点P的坐标和直线AB的表达式;
(2)求四边形AOCP的面积.
解:(1)∵点P(a,2a1)在直线y=3x4上,
∴2a1=3a4,
解得a=3,2a1=5,
∴点P的坐标为(3,5),
将点P(3,5)代入y=kx+8得,
5=3k+8,
解得k=1,
∴直线AB的表达式为:y=x+8;
(2)在一次函数y=3x4中,令x=0,y=4,令x=,y=0,
∴点C的坐标为(,0),
在一次函数y=x+8中,令x=0,y=8,
∴点A的坐标为(0,8),
∴AD=8(4)=18,点P到y轴的距离为3,
四边形AOCP的面积=S△ADPS△DOC
=×3ADOD·OC
=×3×12××4=.
18、为了调到工人的积极性,某开发商每月给工人发的薪酬都是根据当月劳动时间所得奖励加上
基本工资.若某工人每月的劳动时间为x小时,该月可得的总费用为y(元),则y(元)和
x(小时)之间的函数图象如图所示.?
(1)根据图象,请写出某工人每月的基本工资为多少元?开发商是如何奖励工人的?
(2)写出当0≤x≤176时,相应的y与x之间的函数关系式;
(3)若这名工人6月份希望有6570元工资,
则他6月份需工作多少小时?
解:(1)∵x=0时,y=2000,
∴这名工人每月的基本工资为2000元;
如果这名每月工作时间不超过176小时,
每小时获奖励20元;如果这名每月
劳动时间超过176小时,每小时30元奖励.
(2)设当0≤x≤176时,相应的y与x之间的函数关系式为y=kx+2000,
将x=176,y=5520代入y=kx+2000,得5520=176k+2000,
解得k=20,
y与x之间的函数关系式为y=20x+2000;
(3)∵74405520=1920,1920÷(240176)=30,
当x≥176时,设y与x的函数关系式为:y=30x+b.
将x=176,y=5520代入y=30x+b,得5520=30×176+b,
解得b=240,
∴当x≥176时,设y与x的函数关系式为:y=30x+240.
当y=6570时,
由题意得,30x+240=6570
解得
x=211小时,
答:他6月份需工作211小时.
第18题图
第11题图
第2题图
第9题图
第14题图
第2题图
第22题图
第3题图
第20题图
第18题图
第13题图
第4题图
第1题图
第9题图
第13题图
A
B
C
D
第17题图
第19题图
第16题图
第17题图
第10题图
第16题图
第21题图
第16题图
A
B
C
D
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
