11.1_全等三角形
图片预览

文档简介
全等三角形 达标训练1
基础·巩固·达标
1.下列说法正确的是( )
A.形状相同的两个三角形全等 B.面积相等的两个三角形全等 C.完全重合的两个三角形全等 D.所有的等边三角形全等
思路解析:形状和大小完全相同,能够重合的三角形全等;面积相等只跟三角形的底与高的乘积有关,与形状无关;若边长不同,则等边三角形不全等.
答案:C
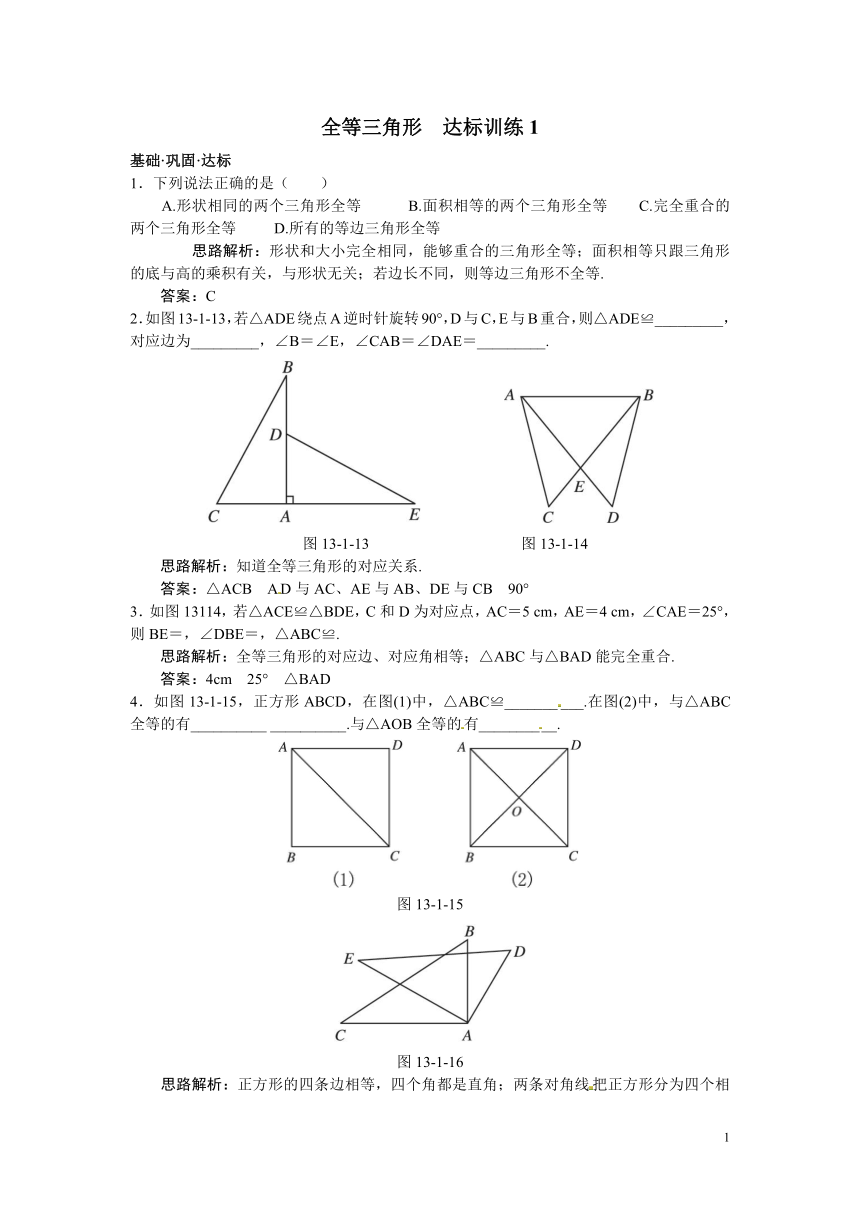
2.如图13-1-13,若△ADE绕点A逆时针旋转90°,D与C,E与B重合,则△ADE≌_________,对应边为_________,∠B=∠E,∠CAB=∠DAE=_________.
图13-1-13 图13-1-14
思路解析:知道全等三角形的对应关系.
答案:△ACB AD与AC、AE与AB、DE与CB 90°
3.如图13114,若△ACE≌△BDE,C和D为对应点,AC=5 cm,AE=4 cm,∠CAE=25°,则BE=,∠DBE=,△ABC≌.
思路解析:全等三角形的对应边、对应角相等;△ABC与△BAD能完全重合.
答案:4cm 25° △BAD
4.如图13-1-15,正方形ABCD,在图(1)中,△ABC≌__________.在图(2)中,与△ABC全等的有__________ __________.与△AOB全等的有__________.
图13-1-15
图13-1-16
思路解析:正方形的四条边相等,四个角都是直角;两条对角线把正方形分为四个相同的小直角三角形.
答案:△ADC △ADC、△DAB、△DCB △AOD、△DOC、△COB
5.如图13-1-16,△ABC≌△ADE,∠DAC=120°,∠DAB=30°,则∠CAE=__________,∠EAB=__________.
图13-1-7
思路解析:全等三角形的对应角相等.
答案:30° 60°
6.如图13-1-17是某房间木地板的一个图案,其中AB=BC=CD=DA,AE=CE=CF=FA,图案是由有花纹是全等三角形木板(阴影部分)与无花纹的全等三角形木板(中间部分)拼成.这个图案的面积是0.05 m2,若房间的面积是13 m2,那么最少需要有花纹的三角形木板和无花纹的木板各多少块?
思路解析:六个部分组成一个图案,把一个图案作为一个整体,每个图案的面积已知,还知道房间的总面积,可以计算出这种图案的个数.而每个图案由6个三角形木板组成,可以分别计算出每种三角形木板的块数.
解:图案的总个数为:13÷0.05=260(块).
因为一个图案由4块全等的有花纹三角形木块与2块全等的无花纹的木块拼成,且全等三角形的面积相等,
所以,花纹三角形木板的个数为:260×4=1 040(块).
无花纹三角形木板的个数为:260×2=520(块).
答:至少需要有花纹的三角形木块1 040块,无花纹三角形木块520块.
综合·应用·创新
图13-1-18
7.如图13-1-18,△ABC≌△DBE,问AE与DC有什么关系?为什么?
图13-1-19
思路解析:全等三角形的对应边相等,而AB=AE+BE,DB=BC+DC.
答案:相等.
理由:∵△ABC≌△DBE,∴AB=DB,BC=BE.∴AB-BE=DB-BC.∴AE=DC.
8.如图13-1-19,已知△ABC≌△DEF,∠A=70°,∠B=60°,BF=2.
(1)求∠DFE的度数和EC的长;
(2)在图13-1-19中,△EDF可以通过平移、翻折、旋转中的哪些方法变到△BAC的位置?
图13-1-20
答案:(1)50°,2;(2)绕F点旋转180°后,沿直线BC向上平移线段CF的长度.
9.如图13-1-20,将△ABC绕点A顺时针旋转30°后得△AB1C1,将△ABC沿直线AB翻折得△ABC2. (1)问△AB1C1与△ABC2有何关系?
(2)求∠CAC1的度数.
思路解析:因为一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小没有改变,即平移、翻折、旋转前后的图形全等.
解:(1)由题意得△AB1C1≌△ABC,△ABC≌△ABC2,
∴△AB1C1≌△ABC2.
(2)∵△AB1C1≌△ABC,
∴∠B1AC1=∠BAC. ∴∠B1AC1-∠B1AC=∠BAC-∠B1AC,
即∠CAC1=∠BAB1=30°.
10.用一个边长为10 cm的正方形纸板,剪出七巧板,并找出其中全等的三角形.
思路解析:七巧板的组成如下图.
答案:如上图,全等三角形有两对.
回顾·热身·展望
11.湖北宜昌模拟 观察图13-1-21中的各个图形,其中的全等图形为(图形用编号表示):.
图13-1-21
思路解析:①和⑥、②和⑤、③和⑧它们各组图形的形状完全一样,通过平移、旋转后,能够完全重合,所以是全等形.将图形叠合来判断是否全等,直观形象,但有时不方便,借助网格背景来观察比较,是一种非常方便有效的方法.
解:①和⑥、②和⑤、③和⑧分别为全等的图形.
PAGE
1
基础·巩固·达标
1.下列说法正确的是( )
A.形状相同的两个三角形全等 B.面积相等的两个三角形全等 C.完全重合的两个三角形全等 D.所有的等边三角形全等
思路解析:形状和大小完全相同,能够重合的三角形全等;面积相等只跟三角形的底与高的乘积有关,与形状无关;若边长不同,则等边三角形不全等.
答案:C
2.如图13-1-13,若△ADE绕点A逆时针旋转90°,D与C,E与B重合,则△ADE≌_________,对应边为_________,∠B=∠E,∠CAB=∠DAE=_________.
图13-1-13 图13-1-14
思路解析:知道全等三角形的对应关系.
答案:△ACB AD与AC、AE与AB、DE与CB 90°
3.如图13114,若△ACE≌△BDE,C和D为对应点,AC=5 cm,AE=4 cm,∠CAE=25°,则BE=,∠DBE=,△ABC≌.
思路解析:全等三角形的对应边、对应角相等;△ABC与△BAD能完全重合.
答案:4cm 25° △BAD
4.如图13-1-15,正方形ABCD,在图(1)中,△ABC≌__________.在图(2)中,与△ABC全等的有__________ __________.与△AOB全等的有__________.
图13-1-15
图13-1-16
思路解析:正方形的四条边相等,四个角都是直角;两条对角线把正方形分为四个相同的小直角三角形.
答案:△ADC △ADC、△DAB、△DCB △AOD、△DOC、△COB
5.如图13-1-16,△ABC≌△ADE,∠DAC=120°,∠DAB=30°,则∠CAE=__________,∠EAB=__________.
图13-1-7
思路解析:全等三角形的对应角相等.
答案:30° 60°
6.如图13-1-17是某房间木地板的一个图案,其中AB=BC=CD=DA,AE=CE=CF=FA,图案是由有花纹是全等三角形木板(阴影部分)与无花纹的全等三角形木板(中间部分)拼成.这个图案的面积是0.05 m2,若房间的面积是13 m2,那么最少需要有花纹的三角形木板和无花纹的木板各多少块?
思路解析:六个部分组成一个图案,把一个图案作为一个整体,每个图案的面积已知,还知道房间的总面积,可以计算出这种图案的个数.而每个图案由6个三角形木板组成,可以分别计算出每种三角形木板的块数.
解:图案的总个数为:13÷0.05=260(块).
因为一个图案由4块全等的有花纹三角形木块与2块全等的无花纹的木块拼成,且全等三角形的面积相等,
所以,花纹三角形木板的个数为:260×4=1 040(块).
无花纹三角形木板的个数为:260×2=520(块).
答:至少需要有花纹的三角形木块1 040块,无花纹三角形木块520块.
综合·应用·创新
图13-1-18
7.如图13-1-18,△ABC≌△DBE,问AE与DC有什么关系?为什么?
图13-1-19
思路解析:全等三角形的对应边相等,而AB=AE+BE,DB=BC+DC.
答案:相等.
理由:∵△ABC≌△DBE,∴AB=DB,BC=BE.∴AB-BE=DB-BC.∴AE=DC.
8.如图13-1-19,已知△ABC≌△DEF,∠A=70°,∠B=60°,BF=2.
(1)求∠DFE的度数和EC的长;
(2)在图13-1-19中,△EDF可以通过平移、翻折、旋转中的哪些方法变到△BAC的位置?
图13-1-20
答案:(1)50°,2;(2)绕F点旋转180°后,沿直线BC向上平移线段CF的长度.
9.如图13-1-20,将△ABC绕点A顺时针旋转30°后得△AB1C1,将△ABC沿直线AB翻折得△ABC2. (1)问△AB1C1与△ABC2有何关系?
(2)求∠CAC1的度数.
思路解析:因为一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小没有改变,即平移、翻折、旋转前后的图形全等.
解:(1)由题意得△AB1C1≌△ABC,△ABC≌△ABC2,
∴△AB1C1≌△ABC2.
(2)∵△AB1C1≌△ABC,
∴∠B1AC1=∠BAC. ∴∠B1AC1-∠B1AC=∠BAC-∠B1AC,
即∠CAC1=∠BAB1=30°.
10.用一个边长为10 cm的正方形纸板,剪出七巧板,并找出其中全等的三角形.
思路解析:七巧板的组成如下图.
答案:如上图,全等三角形有两对.
回顾·热身·展望
11.湖北宜昌模拟 观察图13-1-21中的各个图形,其中的全等图形为(图形用编号表示):.
图13-1-21
思路解析:①和⑥、②和⑤、③和⑧它们各组图形的形状完全一样,通过平移、旋转后,能够完全重合,所以是全等形.将图形叠合来判断是否全等,直观形象,但有时不方便,借助网格背景来观察比较,是一种非常方便有效的方法.
解:①和⑥、②和⑤、③和⑧分别为全等的图形.
PAGE
1
