六年级解决问题的策略课件(转化策略)
图片预览



文档简介
(共36张PPT)
解决问题的策略
国标苏教版数学(六下)
武进区南苑小学 李细兴
有一次,爱迪生把一只灯泡交给他的助手阿普顿,让他计算一下这只灯泡的容积是多少。阿普顿是普林顿大学数学系高材生,又在德国深造了一年,数学素养相当不错。他拿着这只梨形的灯泡,打量了好半天,又特地找来皮尺,上下量了尺寸,画出了各种示意图,还列出了一道又一道的算式。一个钟头过去了。爱迪生着急了,跑来问他算出来了没有。“正算到一半。”阿普顿慌忙回答,豆大的汗珠从他的额角上滚了下来。“才算到一半?”爱迪生十分诧异,走近一看,哎呀,在阿普顿的面前,好几张白纸上写满了密密麻麻的算式。“何必这么复杂呢?”爱迪生微笑着说,“你把这只灯泡装满水,再把水倒在量杯里,量杯量出来的水的体积,就是灯泡的容积。”
“哦!”阿普顿恍然大悟。他飞快地跑进实验室,不到1分钟,没有经过任何运算,就把灯泡的容积准确地求出来了。
用转化的策略解决问题
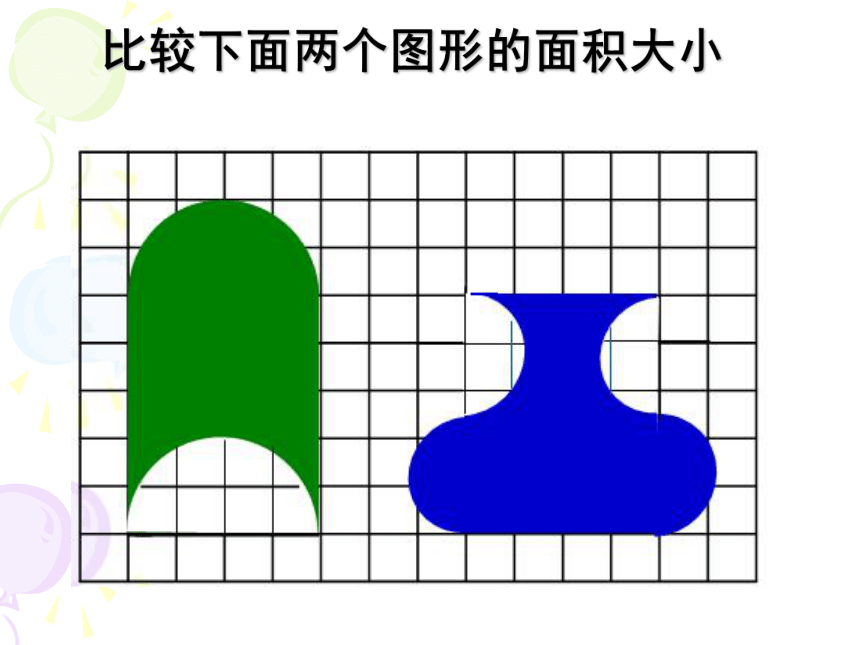
比一比,谁的面积大?
比较下面两个图形的面积大小
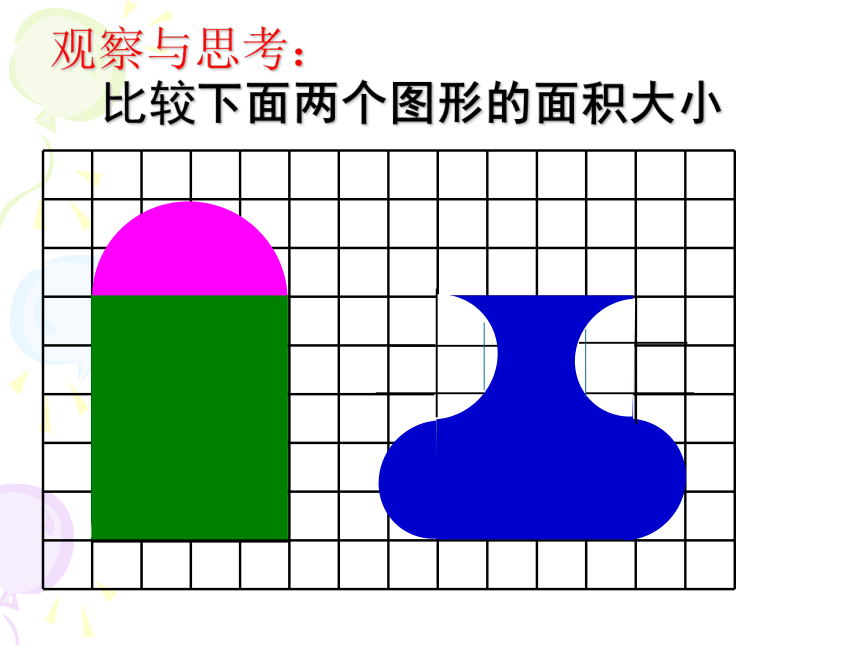
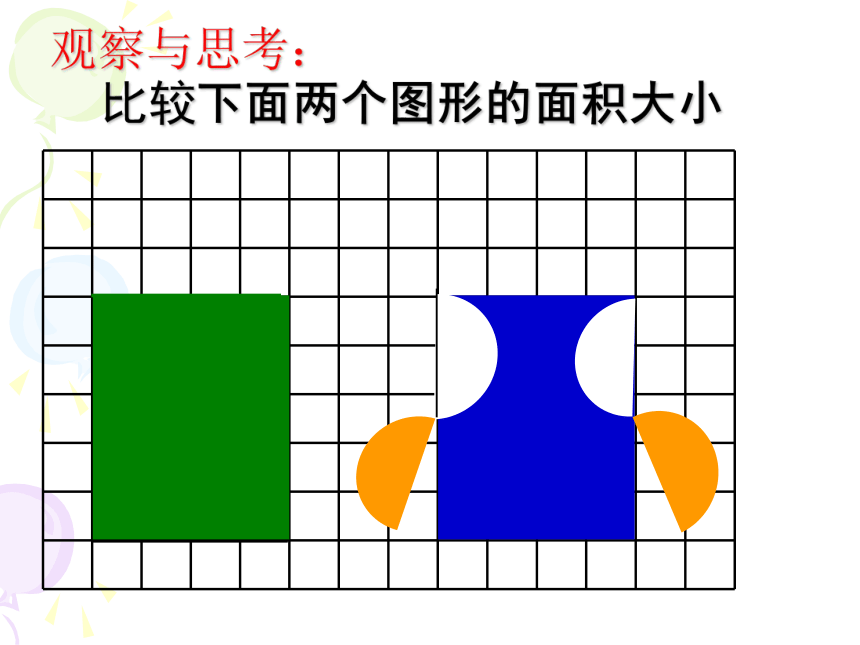
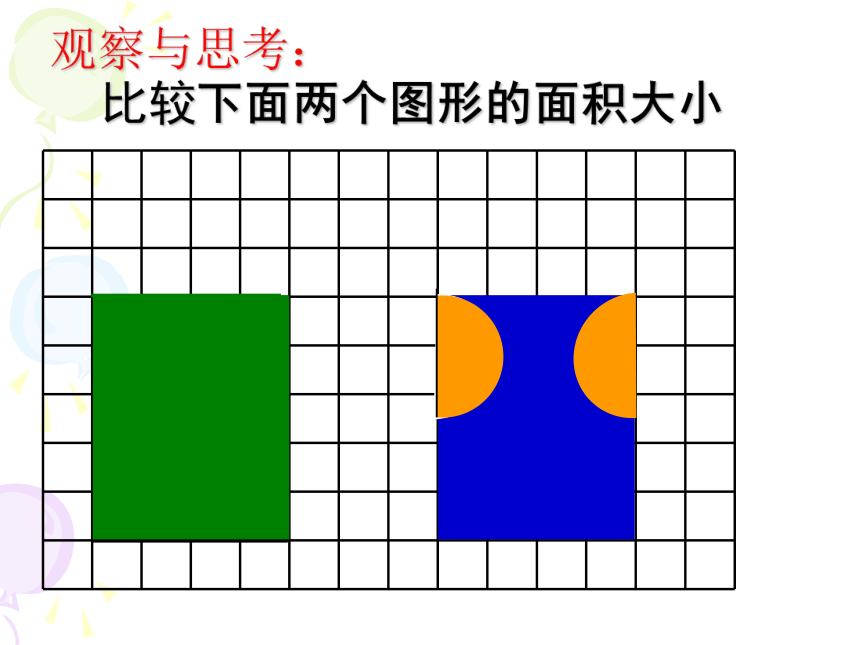
观察与思考:
比较下面两个图形的面积大小
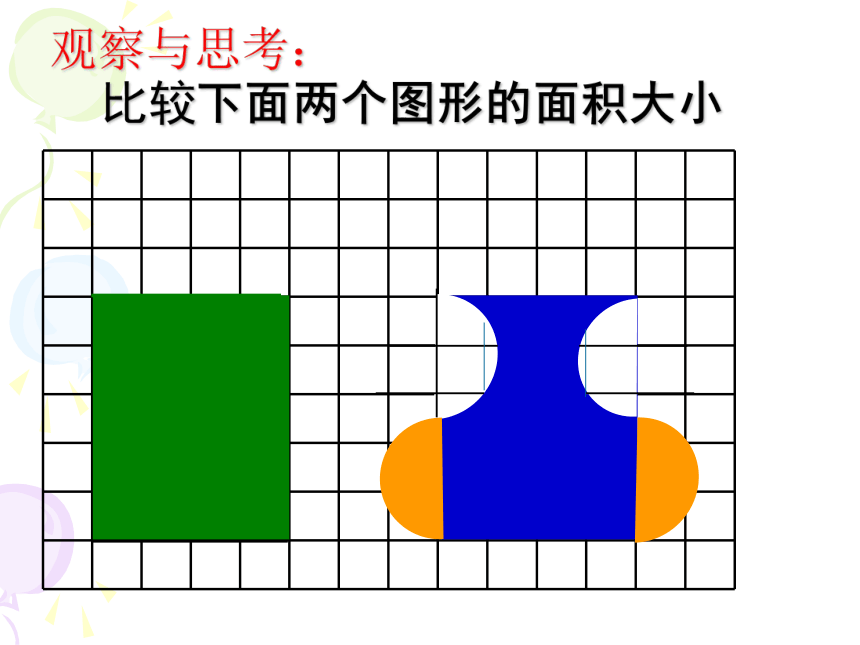
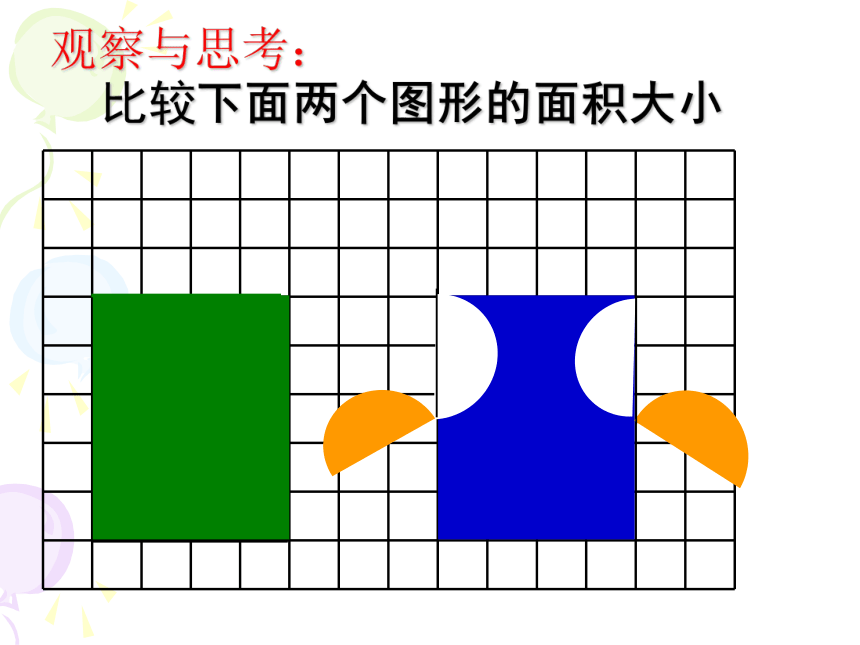
观察与思考:
比较下面两个图形的面积大小
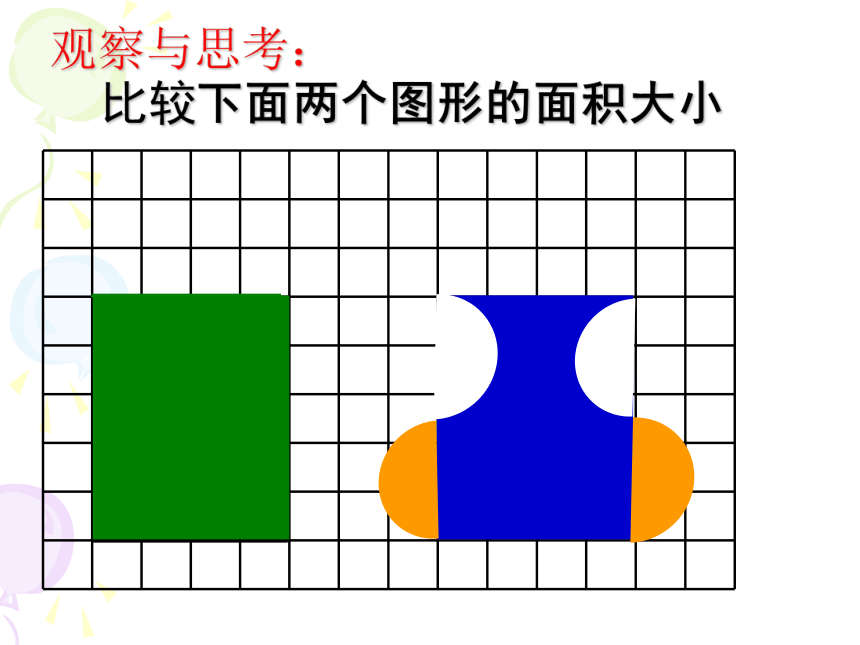
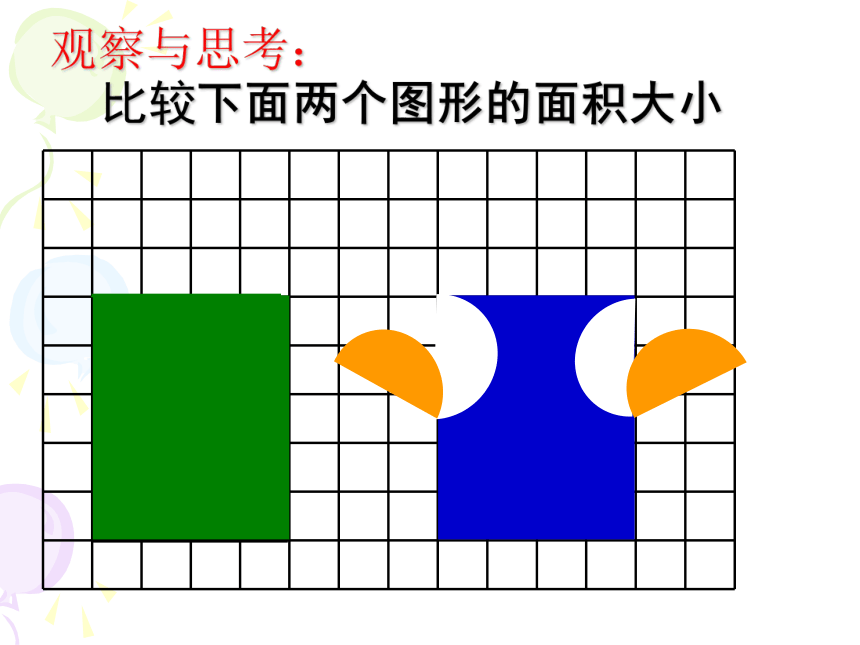
观察与思考:
比较下面两个图形的面积大小
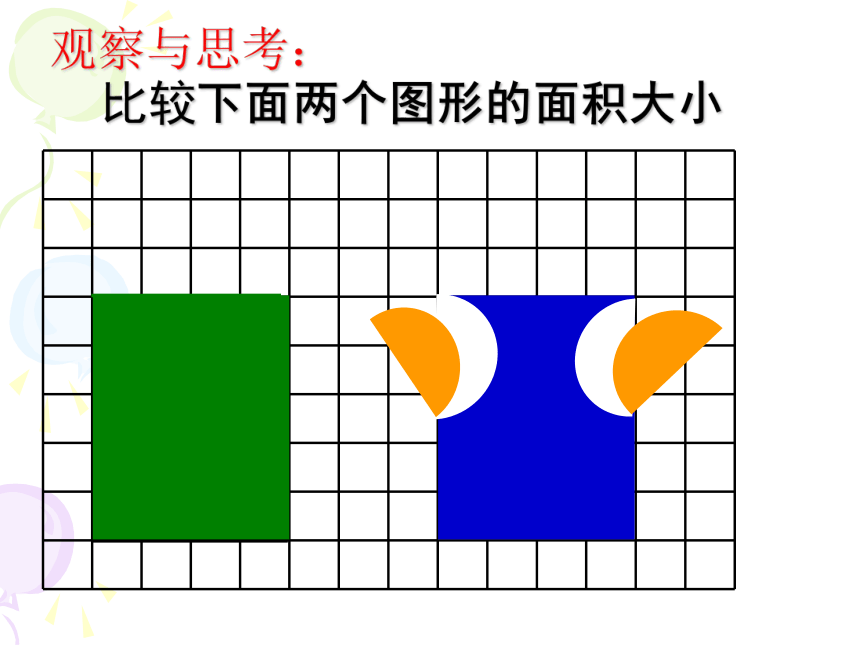
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
转化
回忆:
我们在推导图形的面积或体积公式时用过哪些转化策略?
s平
s三
s圆
v柱
周长
推导平行四边形的面积公式时,把平行四边形转化成长方形。
推导平行四边形的面积公式时,把平行四边形转化成长方形。
返回
返回
用两个完全相同的三角形拼成一个平行四边形。
返回
返回
练习
计算异分母分数加减法时,把异分母分数转化成同分母分数。
涂色
用分数表示各图中的涂色部分
( )
( )
( )
( )
( )
( )
观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便?
每个小方格的边长是1cm,右边图形的周长是多少cm
异分母
抢答智慧题:下面是一个楼梯的剖面图,如果要给这个楼梯铺上地毯,至少需要多少米的地毯?
2米
3.5米
计算下面图形的周长
1m
试一试
1m
1×4=4(m)
返回
黑:4×2×3.14÷2=12.56(m)
红:3.14×4=12.56(m)
返回
试一试:
可以把原式转化成怎样的算式计算?
有16支足球队参加比赛,比赛以单场淘汰制(即每场比赛淘汰1支球队)进行。一共要进行多少场比赛后才能产生冠军?
8+4+2+1=15 (场)
有16支足球队参加比赛,比赛以单场淘汰制进行。一共要进行多少场比赛后才能产生冠军?
返回
16-1=15 (场)
如果有64支球队参加比赛,产 生冠军要比赛多少场?
(要淘汰多少支球队?)
拓展练习:
请计算图中涂色部分的面积。
每个部分的扇形的半径都是 2 厘米。
多位数学家说过:“什么叫解题?解题就是把题目转化为已经解过的题。”
用转化的策略解决问题
解决问题的策略
国标苏教版数学(六下)
武进区南苑小学 李细兴
有一次,爱迪生把一只灯泡交给他的助手阿普顿,让他计算一下这只灯泡的容积是多少。阿普顿是普林顿大学数学系高材生,又在德国深造了一年,数学素养相当不错。他拿着这只梨形的灯泡,打量了好半天,又特地找来皮尺,上下量了尺寸,画出了各种示意图,还列出了一道又一道的算式。一个钟头过去了。爱迪生着急了,跑来问他算出来了没有。“正算到一半。”阿普顿慌忙回答,豆大的汗珠从他的额角上滚了下来。“才算到一半?”爱迪生十分诧异,走近一看,哎呀,在阿普顿的面前,好几张白纸上写满了密密麻麻的算式。“何必这么复杂呢?”爱迪生微笑着说,“你把这只灯泡装满水,再把水倒在量杯里,量杯量出来的水的体积,就是灯泡的容积。”
“哦!”阿普顿恍然大悟。他飞快地跑进实验室,不到1分钟,没有经过任何运算,就把灯泡的容积准确地求出来了。
用转化的策略解决问题
比一比,谁的面积大?
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
观察与思考:
比较下面两个图形的面积大小
转化
回忆:
我们在推导图形的面积或体积公式时用过哪些转化策略?
s平
s三
s圆
v柱
周长
推导平行四边形的面积公式时,把平行四边形转化成长方形。
推导平行四边形的面积公式时,把平行四边形转化成长方形。
返回
返回
用两个完全相同的三角形拼成一个平行四边形。
返回
返回
练习
计算异分母分数加减法时,把异分母分数转化成同分母分数。
涂色
用分数表示各图中的涂色部分
( )
( )
( )
( )
( )
( )
观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便?
每个小方格的边长是1cm,右边图形的周长是多少cm
异分母
抢答智慧题:下面是一个楼梯的剖面图,如果要给这个楼梯铺上地毯,至少需要多少米的地毯?
2米
3.5米
计算下面图形的周长
1m
试一试
1m
1×4=4(m)
返回
黑:4×2×3.14÷2=12.56(m)
红:3.14×4=12.56(m)
返回
试一试:
可以把原式转化成怎样的算式计算?
有16支足球队参加比赛,比赛以单场淘汰制(即每场比赛淘汰1支球队)进行。一共要进行多少场比赛后才能产生冠军?
8+4+2+1=15 (场)
有16支足球队参加比赛,比赛以单场淘汰制进行。一共要进行多少场比赛后才能产生冠军?
返回
16-1=15 (场)
如果有64支球队参加比赛,产 生冠军要比赛多少场?
(要淘汰多少支球队?)
拓展练习:
请计算图中涂色部分的面积。
每个部分的扇形的半径都是 2 厘米。
多位数学家说过:“什么叫解题?解题就是把题目转化为已经解过的题。”
用转化的策略解决问题
