人教版数学七年级上册课件:4.3.3余角和补角(共23张PPT)
文档属性
| 名称 | 人教版数学七年级上册课件:4.3.3余角和补角(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-09 06:58:15 | ||
图片预览







文档简介
(共23张PPT)
课前小测
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
4.3.3余角与补角
第四章
几何图形初步
新人教版七年级数学上册
学习目标
1、认识一个角的余角与补角,并能熟练求出一个角的余角与补角。
2、经历探究余角与补角的性质,并会用其性质解决一些简单的问题。
1
2
一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了几个角?
3
4
∠1与∠2有什么数量关系?
∠3与∠4又有什么数量关系?
∠1+∠2=90°
∠3+∠4=180°
如果两个角的和为90°
(直角),那么称这两个角
互为余角
,简称“互余”。
1
2
3
4
如果两个角的和为180°(平角),那么称这两个角
互为补角,简称“互补”。
你问我答
游戏规则如下:
其中一个同学任意说出一个0°—
180°之间的角,并说明你想知道的是它的余角或补角,其他同学抢答。
问题:
1、钝角有没有余角?
2、直角有没有补角?
3、∠α的余角可表示为________,
补角可表示为__________。
90°-
α
180°-
α
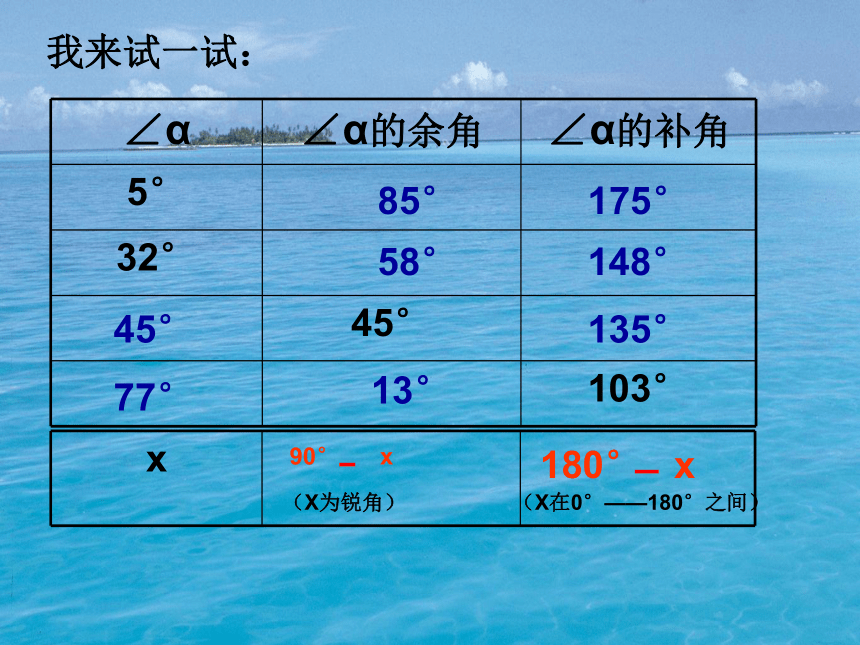
我来试一试:
∠α
∠α的余角
∠α的补角
5°
32°
45°
103°
85°
175°
58°
148°
45°
135°
77°
13°
x
90°
x
180°
x
(X为锐角)
(X在0°——180°之间)
判断
4)如果∠1=30°,∠2=25°,∠3=35°,那么∠1、∠2、∠3这三个角互为余角.
(
)
2)一个角的补角一定比这个角大。(
)
3)互余的两个角一定都是锐角,两个锐角一定互余.
(
)
1)一个角的补角必为钝角。
(
)
×
×
×
×
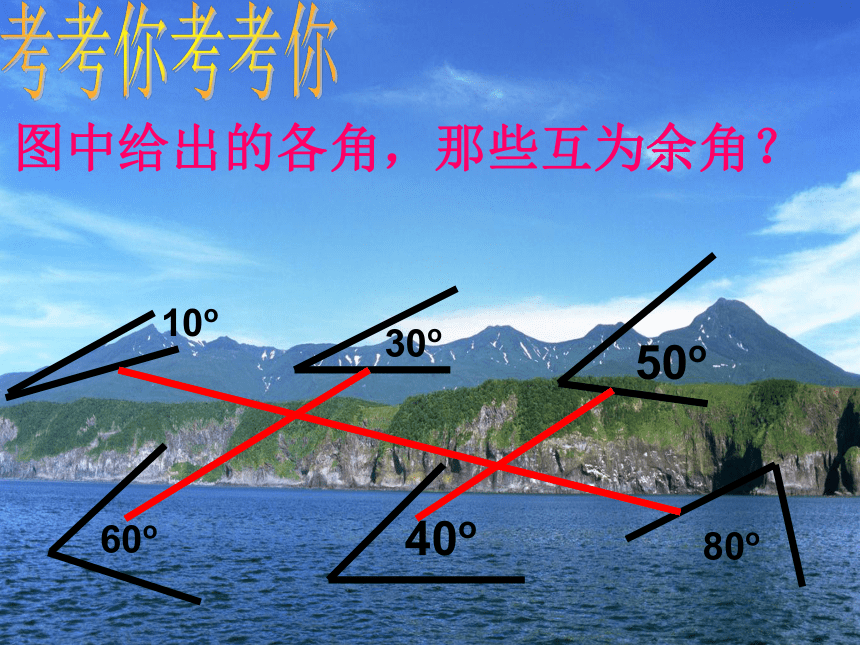
考考你
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
考考你
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
余角、补角与两个角的大小有关系,与它们的位置没有关系。
B
A
O
C
如图两堵墙围一个
角
,但人不能进入围墙,我们如何去测这个角的大小呢?
动动脑
三、开动脑筋
互余
互补
两角间的数量
关系
对应
图形
性质
同角或等角的
余角相等
同角或等角的
补角相等
同角的余角相等
探究一
∴∠2=∠3
∵∠1与∠
2互余
∠
2=
90
°-
∠1
∵∠1与∠3互余
∠3=
90
°-
∠1
∠1与∠
2互为余角,∠1与∠3互余,
∠
2与∠
3大小有什么关系
B
O
C
A
D
2
1
3
结论:
∴
∴
如图,∠1和∠2互余,∠3和∠4互余,若∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
同角(等角)的余角相等。
理由:∵∠1与∠2互余
∴∠2=90o-∠1
∵∠3与∠4互余
∴∠4=90o-∠3
又∵∠1=∠3
∴∠2=∠4
解:
∠2与∠4相等
探究二
结论:
等角的余角相等
余角的性质:
补角的性质:
同角(等角)的补角相等。
新知运用
C
59°20
’
相等
等角的补角相等
今天我们学了什么?
(1)余角、补角的概念
余角、补角与两个角的大小有关系,与它们的位置没有关系。
(2)余角、补角的性质
同(等)角的余角相等;
同(等)角的补角相等。
达标检测
1、下列说法中错误的是(
)
A.互余的两个角都是锐角
B.两角互余、互补与这两角的大小有关,与两角的位置无关
C.互为补角的两个角不可能都是钝角
D.互为补角的两个角一个是锐角,另一个是钝角
D
C
40°
130°
144°38
’
<1与<2与<1与<
COD
<2与已知一个角的补角是这个角的余角的4倍,求这个角的度数。
解:设这个角为x°,那么它的余角为(90-x)
°,它的补角为(180-x)
°,则
180-x=4(90-x)
开动脑筋
解得x=60
答:这个角是60o。
课前小测
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
4.3.3余角与补角
第四章
几何图形初步
新人教版七年级数学上册
学习目标
1、认识一个角的余角与补角,并能熟练求出一个角的余角与补角。
2、经历探究余角与补角的性质,并会用其性质解决一些简单的问题。
1
2
一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了几个角?
3
4
∠1与∠2有什么数量关系?
∠3与∠4又有什么数量关系?
∠1+∠2=90°
∠3+∠4=180°
如果两个角的和为90°
(直角),那么称这两个角
互为余角
,简称“互余”。
1
2
3
4
如果两个角的和为180°(平角),那么称这两个角
互为补角,简称“互补”。
你问我答
游戏规则如下:
其中一个同学任意说出一个0°—
180°之间的角,并说明你想知道的是它的余角或补角,其他同学抢答。
问题:
1、钝角有没有余角?
2、直角有没有补角?
3、∠α的余角可表示为________,
补角可表示为__________。
90°-
α
180°-
α
我来试一试:
∠α
∠α的余角
∠α的补角
5°
32°
45°
103°
85°
175°
58°
148°
45°
135°
77°
13°
x
90°
x
180°
x
(X为锐角)
(X在0°——180°之间)
判断
4)如果∠1=30°,∠2=25°,∠3=35°,那么∠1、∠2、∠3这三个角互为余角.
(
)
2)一个角的补角一定比这个角大。(
)
3)互余的两个角一定都是锐角,两个锐角一定互余.
(
)
1)一个角的补角必为钝角。
(
)
×
×
×
×
考考你
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
考考你
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
余角、补角与两个角的大小有关系,与它们的位置没有关系。
B
A
O
C
如图两堵墙围一个
角
,但人不能进入围墙,我们如何去测这个角的大小呢?
动动脑
三、开动脑筋
互余
互补
两角间的数量
关系
对应
图形
性质
同角或等角的
余角相等
同角或等角的
补角相等
同角的余角相等
探究一
∴∠2=∠3
∵∠1与∠
2互余
∠
2=
90
°-
∠1
∵∠1与∠3互余
∠3=
90
°-
∠1
∠1与∠
2互为余角,∠1与∠3互余,
∠
2与∠
3大小有什么关系
B
O
C
A
D
2
1
3
结论:
∴
∴
如图,∠1和∠2互余,∠3和∠4互余,若∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
同角(等角)的余角相等。
理由:∵∠1与∠2互余
∴∠2=90o-∠1
∵∠3与∠4互余
∴∠4=90o-∠3
又∵∠1=∠3
∴∠2=∠4
解:
∠2与∠4相等
探究二
结论:
等角的余角相等
余角的性质:
补角的性质:
同角(等角)的补角相等。
新知运用
C
59°20
’
相等
等角的补角相等
今天我们学了什么?
(1)余角、补角的概念
余角、补角与两个角的大小有关系,与它们的位置没有关系。
(2)余角、补角的性质
同(等)角的余角相等;
同(等)角的补角相等。
达标检测
1、下列说法中错误的是(
)
A.互余的两个角都是锐角
B.两角互余、互补与这两角的大小有关,与两角的位置无关
C.互为补角的两个角不可能都是钝角
D.互为补角的两个角一个是锐角,另一个是钝角
D
C
40°
130°
144°38
’
COD
<2与
解:设这个角为x°,那么它的余角为(90-x)
°,它的补角为(180-x)
°,则
180-x=4(90-x)
开动脑筋
解得x=60
答:这个角是60o。
