六年级上册数学课件-4.1 选择策略解决实际问题 苏教版 (共24张PPT)
文档属性
| 名称 | 六年级上册数学课件-4.1 选择策略解决实际问题 苏教版 (共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-09 00:00:00 | ||
图片预览





文档简介
选择策略解决实际问题
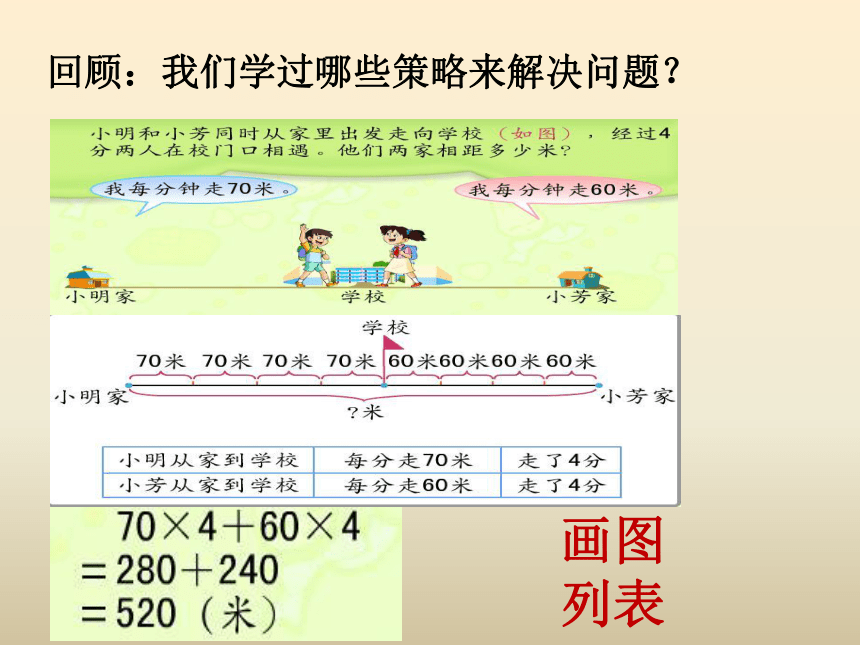
回顾:我们学过哪些策略来解决问题?
列表
回顾:我们学过哪些策略来解决问题?
画图
列表
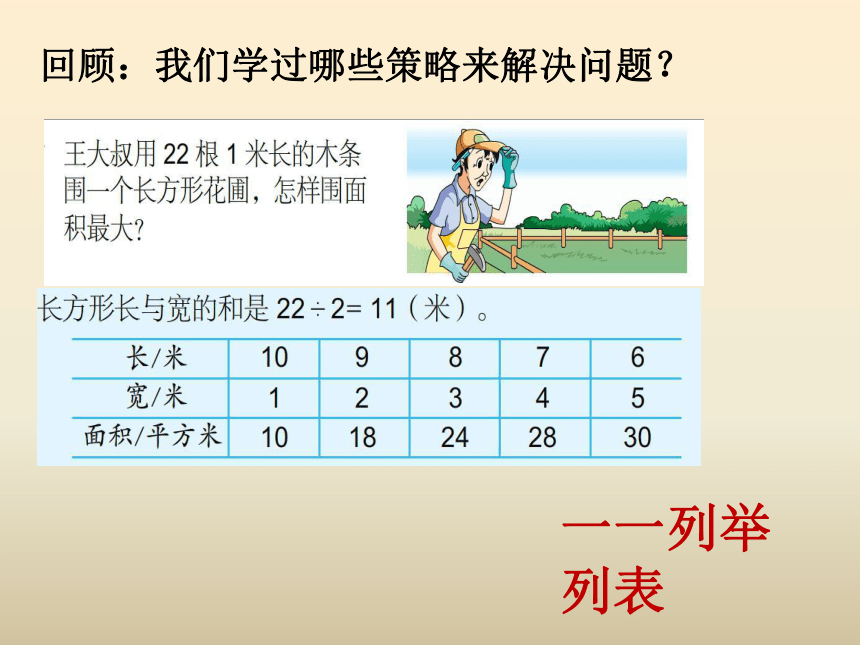
回顾:我们学过哪些策略来解决问题?
一一列举
列表
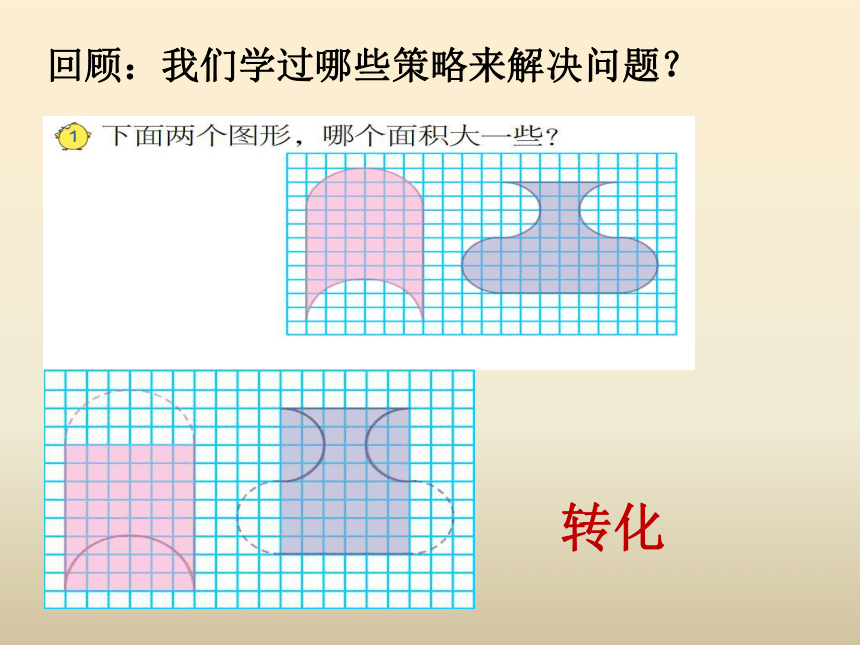
回顾:我们学过哪些策略来解决问题?
转化
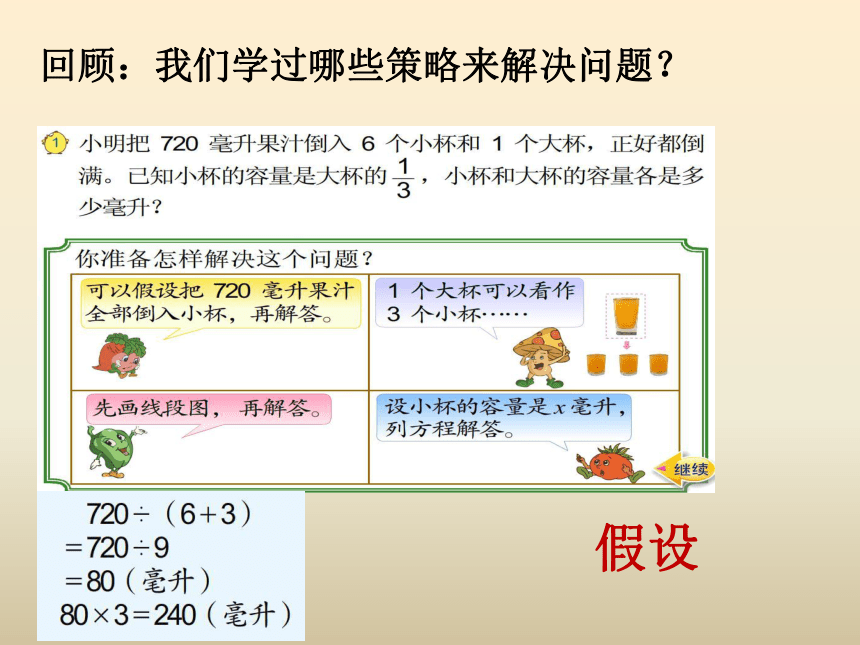
回顾:我们学过哪些策略来解决问题?
假设
预习检测
根据下面的分数和比,你能想到些什么?
1.果园里苹果树与梨树棵树的比是4:3。
2.一瓶果汁,喝了 。
自主学习
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
小组合作:
1.独立思考,你打算用什么策略来解决问题?
2.把你的想法和小组内的同学交流。
3.小组内每人选择一种方法进行解答,并检验。
解:设星河小学美术组总人数为χ人。
总人数-男生人数=女生人数
χ - χ=21
χ=35
男生人数:35 - 21=14(人)
答:男生有14人。
将题中的分数关系转化成份数关系。
把总人数看成5份,男生看成2份,女生人数是5-2=3(份)。也就是3份是21人,1份是21÷3=7(人);1份是7人,男生有这样的2份,所以男生是7×2=14(人)
男生人数:21 ÷(5 - 2) ×2
=21 ÷3 ×2
=7 ×2
=14(人)
答:男生有14人。
列综合算式:
检验:
14÷(14+21)
=14÷35
=
将题中的分数关系转化成比的关系。
男生人数占总人数的 。
男生人数和总人数的比是2 ︰5,
女生人数和总人数的比是3 ︰5,
21÷3×2=14(人)。
男生人数与女生人数的比是2 ︰3。
答:男生有14人。
将题中的分数关系转化成比的关系。
男生人数占总人数的 。
男生人数和总人数的比是2 ︰5,女生人数和总人数的比是3 ︰5,
男生人数与女生人数的比是2 ︰3。
男生人数是女生人数的 。
男生人数是女生人数的 。
21 × =14(人)
答:男生有14人。
女生人数是“单位1”
男生人数是女生人数的 。
求一个数是另一个数的几分之几?用乘法计算。
男生人数:21 × =14(人)
答:男生有14人。
列式计算:
各种策略的特点:
1.画图策略:能使数量关系更直观,更清楚。
2.分数转化成比策略:更容易理解数量之间的关系。
3.解方程策略:可以直观的将题目中的等量关系表现出来。
4.转化单位“1”策略:能够运用分数乘除法快速解答。
练习五
2
5
3
5
2
3
7
5
2
7
2
5
同学们,这节课你学习了什么?你有哪些收获和体会?
课堂总结
什么叫解题?
解题时,往往不对问题进行
正面的攻击,而是将它不断
变形,直至转化为已经能够
解决的问题。
— 数学家 路莎·彼得
每日一题
小明读一本书,已读的页数是未读页数的 ,
他再读30页,这时已读页数是未读页数的 ,
这本书有多少页?
回顾:我们学过哪些策略来解决问题?
列表
回顾:我们学过哪些策略来解决问题?
画图
列表
回顾:我们学过哪些策略来解决问题?
一一列举
列表
回顾:我们学过哪些策略来解决问题?
转化
回顾:我们学过哪些策略来解决问题?
假设
预习检测
根据下面的分数和比,你能想到些什么?
1.果园里苹果树与梨树棵树的比是4:3。
2.一瓶果汁,喝了 。
自主学习
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
小组合作:
1.独立思考,你打算用什么策略来解决问题?
2.把你的想法和小组内的同学交流。
3.小组内每人选择一种方法进行解答,并检验。
解:设星河小学美术组总人数为χ人。
总人数-男生人数=女生人数
χ - χ=21
χ=35
男生人数:35 - 21=14(人)
答:男生有14人。
将题中的分数关系转化成份数关系。
把总人数看成5份,男生看成2份,女生人数是5-2=3(份)。也就是3份是21人,1份是21÷3=7(人);1份是7人,男生有这样的2份,所以男生是7×2=14(人)
男生人数:21 ÷(5 - 2) ×2
=21 ÷3 ×2
=7 ×2
=14(人)
答:男生有14人。
列综合算式:
检验:
14÷(14+21)
=14÷35
=
将题中的分数关系转化成比的关系。
男生人数占总人数的 。
男生人数和总人数的比是2 ︰5,
女生人数和总人数的比是3 ︰5,
21÷3×2=14(人)。
男生人数与女生人数的比是2 ︰3。
答:男生有14人。
将题中的分数关系转化成比的关系。
男生人数占总人数的 。
男生人数和总人数的比是2 ︰5,女生人数和总人数的比是3 ︰5,
男生人数与女生人数的比是2 ︰3。
男生人数是女生人数的 。
男生人数是女生人数的 。
21 × =14(人)
答:男生有14人。
女生人数是“单位1”
男生人数是女生人数的 。
求一个数是另一个数的几分之几?用乘法计算。
男生人数:21 × =14(人)
答:男生有14人。
列式计算:
各种策略的特点:
1.画图策略:能使数量关系更直观,更清楚。
2.分数转化成比策略:更容易理解数量之间的关系。
3.解方程策略:可以直观的将题目中的等量关系表现出来。
4.转化单位“1”策略:能够运用分数乘除法快速解答。
练习五
2
5
3
5
2
3
7
5
2
7
2
5
同学们,这节课你学习了什么?你有哪些收获和体会?
课堂总结
什么叫解题?
解题时,往往不对问题进行
正面的攻击,而是将它不断
变形,直至转化为已经能够
解决的问题。
— 数学家 路莎·彼得
每日一题
小明读一本书,已读的页数是未读页数的 ,
他再读30页,这时已读页数是未读页数的 ,
这本书有多少页?
