3.1 探究动能变化与功的关系 课件18张PPT
文档属性
| 名称 | 3.1 探究动能变化与功的关系 课件18张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 311.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-09 00:00:00 | ||
图片预览






文档简介
探究外力做功与物体动能变化的关系
——动能定理
学习目标:
3、会用动能定理解决力学题,知道用动能定理解题的步骤。
1、理解动能定理,知道动能定理的适用条件,会用动能定理进行计算。
2、理解动能定理的推导过程。
1、概念:物体由于运动具有的能量叫做动能。
一、动能
物体的运动速度越快,质量越大,动能越大。
2、定义:物理学中把物体的质量与它的速度平方乘积的一半定义为物体的动能,用Ek表示,即:
1
2
Ek= mv2
定义式:
3、性质:
动能是描述物体运动状态的物理量。
动能是标量,只有大小,没有方向。
单位:“焦耳” (J )
1、关于动和能的关系,正确的是:
A.能是物体具有做功的本领
B.功是能量转化的量度
C.功是在物体状态发生变化过程中的过程量,能是物体的状态量.
D.动和能具有相同的单位,它们的意义完全相同.
2、对于一定质量的物体,正确的说法是:
A、物体质量发生变化,动能也一定变化。
B、物体速度不变,动能也一定不变。
C、物体动能发生变化,速度也一定变化。
D、物体动能不变,速度也一定不变。
练习:
3、改变汽车的质量和速度,都能使汽车的动能发生变化,在下面几种情况中,汽车的动能是原来2倍的是:
A、质量不变,速度变为原来的2倍
B、质量和速度都变为原来的2倍
C、质量减半,速度变为原来的2倍
D、质量变为原来2倍,速度减半
4、关于动能的理解,下列说法正确的是:
A、动能不变的物体,一定处于平衡状态
B、动能不可能是负的
C、一定质量的物体,动能变化时,速度一定变化;但速度变化时,动能不一定变化
D、物体的加速度为零,其动能不变
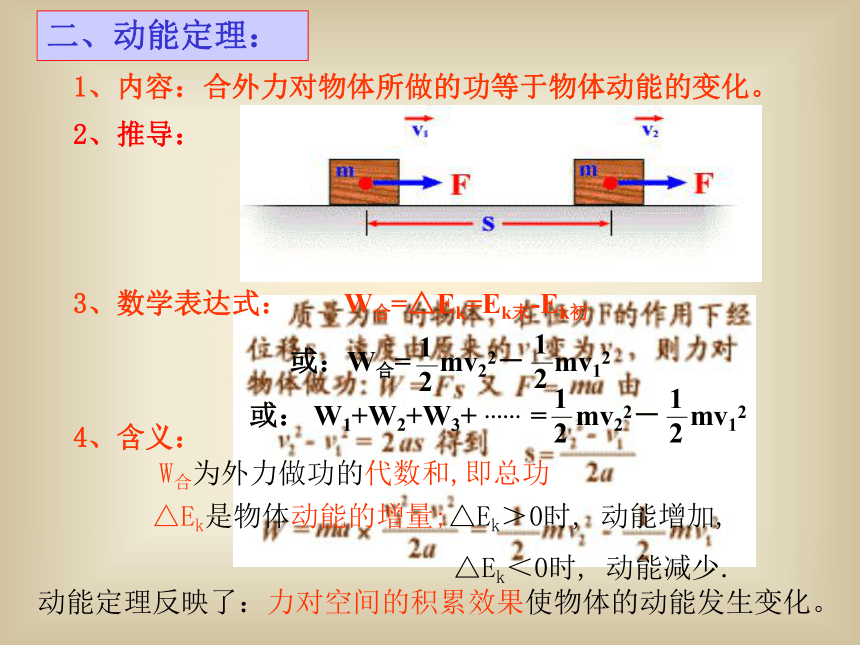
1、内容:合外力对物体所做的功等于物体动能的变化。
2、推导:
二、动能定理:
3、数学表达式:
W合=△Ek=Ek末-Ek初
或:W合= mv22- mv12
1
2
1
2
或: W1+W2+W3+ …… = mv22- mv12
1
2
1
2
△Ek是物体动能的增量;△Ek>0时, 动能增加,
△Ek<0时, 动能减少.
4、含义:
动能定理反映了:力对空间的积累效果使物体的动能发生变化。
W合为外力做功的代数和,即总功
例1.A、B两物体放在光滑的水平面上,分别在相同的水平恒力作用下,由静止开始通过相同的位移,若A的质量大于B的质量,则在这一过程中:
A.A获得的动能大
B.B获得的动能大
C.A、B获得的动能一样大
D.无法比较谁获得的动能大
例2.一辆质量为m、速度为v0的汽车在关闭发动机后在水平地面上滑行了距离l后停下,试求汽车受到的阻力F阻大小。
例3.同一物体分别从高度相同,倾角不同的光滑斜面的顶端滑到底端时,相同的物理量是:
A.动能
B.速度
C.速率
D.重力所做的功
三、动能定理的讨论:
W合 =△Ek = Ek末 - Ek初
动能定理说明外力所做的总功是物体动能变化的量度,
其外力可以是一个力,也可以是几个力的合力。
若W>0,Ek2-Ek1>0,即Ek2>Ek1,说明外力为动力,在动力作用下物体作加速运动:即外力对物体做正功,它的值等于物体动能的增加量。反之表示外力作负功,它的值等于物体动能的减小量。
动能定理只涉及物体运动过程中各外力做功的代数和及物体初末两状态的动能;而不考虑运动过程中的各细节情况,如a,t等。因此应用动能定理解题比较方便。尤其是物体在变力 情况下。
若W=0,即Ek2=Ek1,表示外力对物体不作功,物体动能不变。
四、动能定理的应用:
应用范围:可用于恒力,也可用于变力
既适用于直线运动,也适用于曲线运动。
应用动能定理解题的步骤:
⑴确定研究对象,明确它的运动过程; 并建立好模型。
⑵分析物体在运动过程中的受力情况,明确各个力是否做功,是正功还是负功;
⑶明确初状态和末状态的动能(可分段、亦可对整个运动过程).
⑷用W总=△Ek=Ek2 -Ek1列方程求解.
应用动能定理解题的步骤
例2、用拉力F拉一个质量为m的木箱由静止开始在水平冰道上移动了S,拉力F跟木箱前进的方向的夹角为α,木箱与冰道间的动摩擦因数为μ,求木箱获得的速度.
F
FN
f
G
例1、一架飞机,质量m=5.0×103Kg,起飞过程中从静止开始滑跑的路程为S=5.3×102m时,达到起飞速度v=60m/s.在此过程中飞机受到的平均阻力是重量的0.02倍,求飞机受到的牵引力?
例3、物体从高出地面H处自由落下,不计空气阻 力,落至地面掉入沙坑h停止,求物体在沙坑中受到的平均阻力是其重力的多少倍?
H
h
解法一:分过程处理
解法二:整体法
例4、一个质点在一个恒力F作用下由静止开始运动,速度达到V,然后换成一个方向相反大小为3F的恒力作用,经过一段时间后,质点回到出发点,求质点回到原出发点时的速度.
用动能定理解决变力做功的方法:
一般不直接求功,而是先分析动能变化,再由动能定理求功.
[例1]从高为h处水平地抛出一个质量为m的小球,落地点与抛出点水平距离为s,求抛球时人对球所做的功.
[分析和解答]本题中人对球做的功不能用Fs求出,只能通过做功等于小球动能的变化这个关系求,小球初速度为零,抛出时末速度即平抛运动的初速度,v=s /t,所以抛球时所做的功为:
W=mv2/2-0=ms2g/4h
练习:质量为m的汽车,启动后在发动机的功率保持不变的条件下行驶,经时间t前进距离为s后,速度达量大值v,若行驶中受到的阻力大小不 变,求汽车发动机的功率?
[例2]如图4-12所示,质量为m 的物体静放在水平光滑的平台上,系在物体上的绳子跨过光滑的定滑轮由地面以速度v0向右匀速走动的人拉着,设人从地面上且从平台的边缘开始向右行至绳和水平方向成30°角处,在此过程中人所做的功为: A.mv02/2; B.mv02; C.2mv02/3; D.3mv02/8.
可见,用动能定理解决变力做功是一种常用方法,解此类问题关键是分清各力做功情况和初末动能.
[分析和解答]当右段绳与水平夹角为α时,沿着绳子方向的速率知绳子的拉力是变力,若直接用W=Fscosα求功是不可能的,由动能定理可得:人所做的功等于物体动能的增量,即:W=mv22/2-mv21/2
∵v1=0 v2=v0cos30°=√3 v0/2. ∴W=m( √3v0/2)2/2=3mv02/8.
故正确答案是D.
1.动能定理的另一种表示:W合=W1+…=△EK。
2.运用动能定理对复杂过程列式求解的方法:⑴分段列式法;⑵全程列式法。
例1、质量为1kg物体与水平面间摩擦力为5N,在10N水平力作用下由静止开始前进2m后撤去外力,再前进1m,此时物体仍在运动,其速度为多大?物体最终停止运动,其经过的全部位移为多大?
[解答]物体所受外力有先后不同情况,本题设第1 段位移为s1,第2段位移为s2,拉力为F,摩擦力为f,则对第1、第2段运动过程应用动能定理得:
⑴:Fs1-f(s1+s2)= 1/2mvt2-0, ∴vt=√2(Fs1-f(S1+s2)) =√2(10×2-5×(2+1))/1=3.16(m/s).
(2):全部位移:设撤去外力后直到静止的位移为s',则对全过程应用动能定理得:
Fs1-f(s1+s')=0,∴s'= =2(m),则全部位移为s1+s'=(2+2)=4(m).
可见,物体运动有几个过程时,对全程列式较简单,对全程列式时,关键是分清整个过程有哪些力做功,且各力做功应与位移对应,并确定初末态动能.
练习:如图质量为m的物体从高为h斜面由静止滑下,然后在水平面上滑行一段距离后停下来,已知倾角为α,动磨擦因素为μ,求物体滑行的距离?
——动能定理
学习目标:
3、会用动能定理解决力学题,知道用动能定理解题的步骤。
1、理解动能定理,知道动能定理的适用条件,会用动能定理进行计算。
2、理解动能定理的推导过程。
1、概念:物体由于运动具有的能量叫做动能。
一、动能
物体的运动速度越快,质量越大,动能越大。
2、定义:物理学中把物体的质量与它的速度平方乘积的一半定义为物体的动能,用Ek表示,即:
1
2
Ek= mv2
定义式:
3、性质:
动能是描述物体运动状态的物理量。
动能是标量,只有大小,没有方向。
单位:“焦耳” (J )
1、关于动和能的关系,正确的是:
A.能是物体具有做功的本领
B.功是能量转化的量度
C.功是在物体状态发生变化过程中的过程量,能是物体的状态量.
D.动和能具有相同的单位,它们的意义完全相同.
2、对于一定质量的物体,正确的说法是:
A、物体质量发生变化,动能也一定变化。
B、物体速度不变,动能也一定不变。
C、物体动能发生变化,速度也一定变化。
D、物体动能不变,速度也一定不变。
练习:
3、改变汽车的质量和速度,都能使汽车的动能发生变化,在下面几种情况中,汽车的动能是原来2倍的是:
A、质量不变,速度变为原来的2倍
B、质量和速度都变为原来的2倍
C、质量减半,速度变为原来的2倍
D、质量变为原来2倍,速度减半
4、关于动能的理解,下列说法正确的是:
A、动能不变的物体,一定处于平衡状态
B、动能不可能是负的
C、一定质量的物体,动能变化时,速度一定变化;但速度变化时,动能不一定变化
D、物体的加速度为零,其动能不变
1、内容:合外力对物体所做的功等于物体动能的变化。
2、推导:
二、动能定理:
3、数学表达式:
W合=△Ek=Ek末-Ek初
或:W合= mv22- mv12
1
2
1
2
或: W1+W2+W3+ …… = mv22- mv12
1
2
1
2
△Ek是物体动能的增量;△Ek>0时, 动能增加,
△Ek<0时, 动能减少.
4、含义:
动能定理反映了:力对空间的积累效果使物体的动能发生变化。
W合为外力做功的代数和,即总功
例1.A、B两物体放在光滑的水平面上,分别在相同的水平恒力作用下,由静止开始通过相同的位移,若A的质量大于B的质量,则在这一过程中:
A.A获得的动能大
B.B获得的动能大
C.A、B获得的动能一样大
D.无法比较谁获得的动能大
例2.一辆质量为m、速度为v0的汽车在关闭发动机后在水平地面上滑行了距离l后停下,试求汽车受到的阻力F阻大小。
例3.同一物体分别从高度相同,倾角不同的光滑斜面的顶端滑到底端时,相同的物理量是:
A.动能
B.速度
C.速率
D.重力所做的功
三、动能定理的讨论:
W合 =△Ek = Ek末 - Ek初
动能定理说明外力所做的总功是物体动能变化的量度,
其外力可以是一个力,也可以是几个力的合力。
若W>0,Ek2-Ek1>0,即Ek2>Ek1,说明外力为动力,在动力作用下物体作加速运动:即外力对物体做正功,它的值等于物体动能的增加量。反之表示外力作负功,它的值等于物体动能的减小量。
动能定理只涉及物体运动过程中各外力做功的代数和及物体初末两状态的动能;而不考虑运动过程中的各细节情况,如a,t等。因此应用动能定理解题比较方便。尤其是物体在变力 情况下。
若W=0,即Ek2=Ek1,表示外力对物体不作功,物体动能不变。
四、动能定理的应用:
应用范围:可用于恒力,也可用于变力
既适用于直线运动,也适用于曲线运动。
应用动能定理解题的步骤:
⑴确定研究对象,明确它的运动过程; 并建立好模型。
⑵分析物体在运动过程中的受力情况,明确各个力是否做功,是正功还是负功;
⑶明确初状态和末状态的动能(可分段、亦可对整个运动过程).
⑷用W总=△Ek=Ek2 -Ek1列方程求解.
应用动能定理解题的步骤
例2、用拉力F拉一个质量为m的木箱由静止开始在水平冰道上移动了S,拉力F跟木箱前进的方向的夹角为α,木箱与冰道间的动摩擦因数为μ,求木箱获得的速度.
F
FN
f
G
例1、一架飞机,质量m=5.0×103Kg,起飞过程中从静止开始滑跑的路程为S=5.3×102m时,达到起飞速度v=60m/s.在此过程中飞机受到的平均阻力是重量的0.02倍,求飞机受到的牵引力?
例3、物体从高出地面H处自由落下,不计空气阻 力,落至地面掉入沙坑h停止,求物体在沙坑中受到的平均阻力是其重力的多少倍?
H
h
解法一:分过程处理
解法二:整体法
例4、一个质点在一个恒力F作用下由静止开始运动,速度达到V,然后换成一个方向相反大小为3F的恒力作用,经过一段时间后,质点回到出发点,求质点回到原出发点时的速度.
用动能定理解决变力做功的方法:
一般不直接求功,而是先分析动能变化,再由动能定理求功.
[例1]从高为h处水平地抛出一个质量为m的小球,落地点与抛出点水平距离为s,求抛球时人对球所做的功.
[分析和解答]本题中人对球做的功不能用Fs求出,只能通过做功等于小球动能的变化这个关系求,小球初速度为零,抛出时末速度即平抛运动的初速度,v=s /t,所以抛球时所做的功为:
W=mv2/2-0=ms2g/4h
练习:质量为m的汽车,启动后在发动机的功率保持不变的条件下行驶,经时间t前进距离为s后,速度达量大值v,若行驶中受到的阻力大小不 变,求汽车发动机的功率?
[例2]如图4-12所示,质量为m 的物体静放在水平光滑的平台上,系在物体上的绳子跨过光滑的定滑轮由地面以速度v0向右匀速走动的人拉着,设人从地面上且从平台的边缘开始向右行至绳和水平方向成30°角处,在此过程中人所做的功为: A.mv02/2; B.mv02; C.2mv02/3; D.3mv02/8.
可见,用动能定理解决变力做功是一种常用方法,解此类问题关键是分清各力做功情况和初末动能.
[分析和解答]当右段绳与水平夹角为α时,沿着绳子方向的速率知绳子的拉力是变力,若直接用W=Fscosα求功是不可能的,由动能定理可得:人所做的功等于物体动能的增量,即:W=mv22/2-mv21/2
∵v1=0 v2=v0cos30°=√3 v0/2. ∴W=m( √3v0/2)2/2=3mv02/8.
故正确答案是D.
1.动能定理的另一种表示:W合=W1+…=△EK。
2.运用动能定理对复杂过程列式求解的方法:⑴分段列式法;⑵全程列式法。
例1、质量为1kg物体与水平面间摩擦力为5N,在10N水平力作用下由静止开始前进2m后撤去外力,再前进1m,此时物体仍在运动,其速度为多大?物体最终停止运动,其经过的全部位移为多大?
[解答]物体所受外力有先后不同情况,本题设第1 段位移为s1,第2段位移为s2,拉力为F,摩擦力为f,则对第1、第2段运动过程应用动能定理得:
⑴:Fs1-f(s1+s2)= 1/2mvt2-0, ∴vt=√2(Fs1-f(S1+s2)) =√2(10×2-5×(2+1))/1=3.16(m/s).
(2):全部位移:设撤去外力后直到静止的位移为s',则对全过程应用动能定理得:
Fs1-f(s1+s')=0,∴s'= =2(m),则全部位移为s1+s'=(2+2)=4(m).
可见,物体运动有几个过程时,对全程列式较简单,对全程列式时,关键是分清整个过程有哪些力做功,且各力做功应与位移对应,并确定初末态动能.
练习:如图质量为m的物体从高为h斜面由静止滑下,然后在水平面上滑行一段距离后停下来,已知倾角为α,动磨擦因素为μ,求物体滑行的距离?
同课章节目录
- 第一章 怎样研究抛体运动
- 1 飞机投弹与平抛运动
- 2 研究平抛运动的规律
- 3 研究斜抛运动
- 第二章 研究圆周运动
- 1 怎样描述圆周运动
- 2 研究匀速圆周运动的规律
- 3 圆周运动的案例分析
- 4 研究离心现象及其应用
- 第三章 动能的变化与机械功
- 1 探究动能变化跟功的关系
- 2 研究功与功率
- 3 动能定理的应用
- 第四章 能量守恒与可持续发展
- 1 势能的变化与机械功
- 2 研究机械能守恒定律
- 3 能量的转化与守恒
- 4 能源与可持续发展
- 第五章 万有引力与航天
- 1 从托勒密到开普勒
- 2 万有引力定律是怎样发现的
- 3 万有引力定律与天文学的新发现
- 4 飞出地球去
- 第六章 经典力学与现代物理
- 1 经典力学的巨大成就和局限性
- 2 狭义相对论的基本原理
- 3 爱因斯坦心目中的宇宙
- 4 微观世界与量子论
