3.3 动能定理的案例分析 课件16张PPT
文档属性
| 名称 | 3.3 动能定理的案例分析 课件16张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-09 00:00:00 | ||
图片预览





文档简介
动能定理的案例分析
动能定理推导
2ax=v2-v02
联立消去a
动能定理的推导
F=ma
Fx= mv2- mv02
联立消去a
W合=△Ek
不再局限于直线运动,强调初末状态
对动能定理的理解
1.动能定理的理解
三个关系
①数量关系:W合=△Ek.
②单位关系:等式两侧的国际单位都是焦耳
③因果关系:W合是引起物体的△Ek原因.
定理中的“外力”
可以是重力、弹力、摩擦力,也可以是电场力、磁场力或其他力.
定理中涉及多过程
若过程包含了几个运动性质不同的分过程,既可以分段考虑,也可以整个过程考虑。
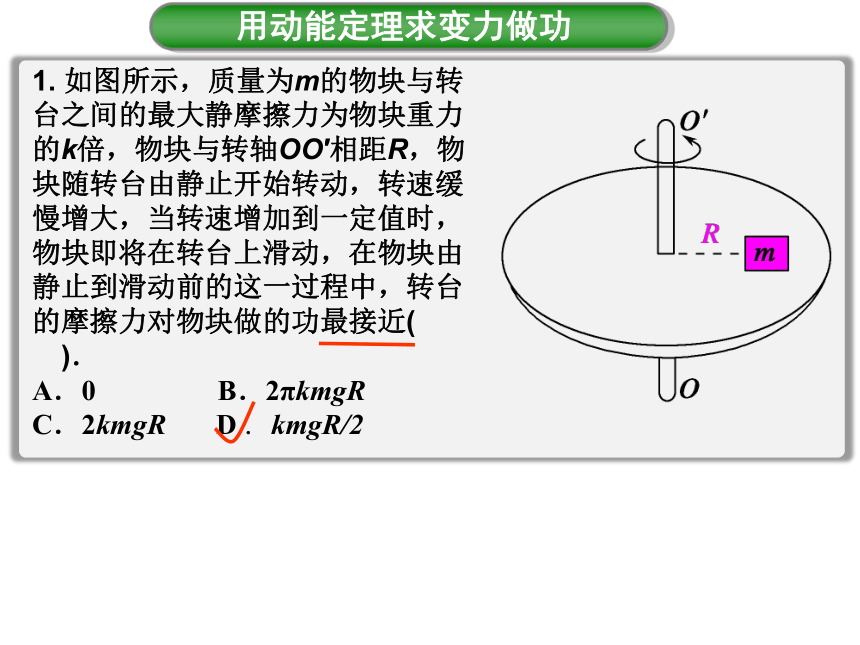
1. 如图所示,质量为m的物块与转台之间的最大静摩擦力为物块重力的k倍,物块与转轴OO′相距R,物块随转台由静止开始转动,转速缓慢增大,当转速增加到一定值时,物块即将在转台上滑动,在物块由静止到滑动前的这一过程中,转台的摩擦力对物块做的功最接近( ).
A.0 B.2πkmgR
C.2kmgR D . kmgR/2
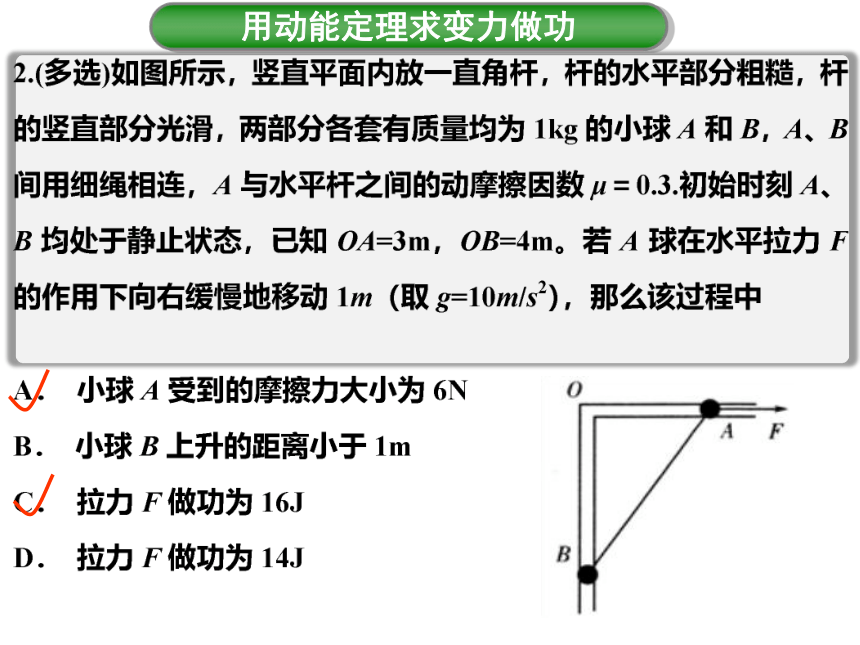
用动能定理求变力做功
用动能定理求变力做功
审题
突破
1.小球由P到A过程中,遵从平抛运动规律及动能定理.
2.小球从A经B到C过程, 遵从动能定理及圆周运动规律.
3. 如图,一个质量为0.6 kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失)。已知圆弧的半径R=0.3 m,θ=60°,小球到达A点时的速度vA=4 m/s。g取10 m/s2,求:
(1)小球做平抛运动的初速度v0;
(2)P点与A点的高度差;
(3)小球到达圆弧最高点C时对轨道的压力。
审题中要注意区分不同过程的受力情况及运动规律.
vA
对动能定理的理解及简单应用
【扩展延伸】
(1)在上题中,求小球经过最低点B时对轨道的压力大小。
(2)在上题中,若圆弧轨道粗糙,小球恰好能够经过最高点C,求此过程小球克服摩擦力所做的功。
vA
对动能定理的理解及简单应用
能优先考虑应用动能定理解答的问题
(1)物理过程中不涉及加速度、时间的问题;
(2)有多个物理过程且不需要研究整个过程中的中间状态的问题;
(3)曲线运动问题,或者变力做功的问题;
(4)含有F、l、m、v、w、Ek等物理量的力学问题.
应用动能定理解题应抓好“一过程,两状态”
“一过程”即明确研究过程,确定这一过程研究对象的受力情况和位置变化或位移信息。
“两状态”即明确研究对象的始、末状态的速度或动能情况。
动能定理在多过程问题中的应用
5. (2015·浙江理综,23)如图示,用一块长L1=1.0 m的木板在墙和桌面间架设斜面,桌子高H=0.8 m,长L2=1.5 m。斜面与水平桌面的倾角θ可在0~60°间调节后固定。将质量m=0.2 kg的小物块从斜面顶端静止释放,物块与斜面间的动摩擦因数μ1=0.05,物块与桌面间的动摩擦因数为μ2,忽略物块在斜面与桌面交接处的能量损失(重力加速度取g=10 m/s2;最大静摩擦力等于滑动摩擦力)
(1)求θ角增大到多少时,物块能从斜面开始下滑;(用正切值表示)
(2)当θ角增大到37°时,物块恰能停在桌面边缘,求物块与桌面间的动摩擦因数μ2;(已知sin 37°=0.6,cos 37°=0.8)
(3)继续增大θ角,发现θ=53°时物块落地点与墙面的距离最大,求此最大距离xm。
动能定理在多过程问题中的应用
[思考题] 某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f.轻杆向右移动不超过l时,装置可安全工作.一质量为m的小车若以速度v0撞击弹簧,将导致轻杆向右移动l/4.轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.
(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度v′和撞击速度v的关系.
审题导析
1.此时弹簧弹力等于滑动摩擦力.
2.对比两次撞击过程,小车的受力、运动、做功有哪些相同之处,哪些不同之处,遵从什么规律?
对动能定理的理解及简单应用
确定研究对象和研究过程
几个力?恒力还是变力?
运动性质及特点
运动分析
受力分析
是否做功?
正功
还是负功?
明确初、末动能
做功 情况
动能 分析
动能 定理
分阶段
或
全过程列方程
解方程
讨论
结果
牛顿运动定律
运动规律
应用动能定理的解题步骤
动能定理推导
2ax=v2-v02
联立消去a
动能定理的推导
F=ma
Fx= mv2- mv02
联立消去a
W合=△Ek
不再局限于直线运动,强调初末状态
对动能定理的理解
1.动能定理的理解
三个关系
①数量关系:W合=△Ek.
②单位关系:等式两侧的国际单位都是焦耳
③因果关系:W合是引起物体的△Ek原因.
定理中的“外力”
可以是重力、弹力、摩擦力,也可以是电场力、磁场力或其他力.
定理中涉及多过程
若过程包含了几个运动性质不同的分过程,既可以分段考虑,也可以整个过程考虑。
1. 如图所示,质量为m的物块与转台之间的最大静摩擦力为物块重力的k倍,物块与转轴OO′相距R,物块随转台由静止开始转动,转速缓慢增大,当转速增加到一定值时,物块即将在转台上滑动,在物块由静止到滑动前的这一过程中,转台的摩擦力对物块做的功最接近( ).
A.0 B.2πkmgR
C.2kmgR D . kmgR/2
用动能定理求变力做功
用动能定理求变力做功
审题
突破
1.小球由P到A过程中,遵从平抛运动规律及动能定理.
2.小球从A经B到C过程, 遵从动能定理及圆周运动规律.
3. 如图,一个质量为0.6 kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失)。已知圆弧的半径R=0.3 m,θ=60°,小球到达A点时的速度vA=4 m/s。g取10 m/s2,求:
(1)小球做平抛运动的初速度v0;
(2)P点与A点的高度差;
(3)小球到达圆弧最高点C时对轨道的压力。
审题中要注意区分不同过程的受力情况及运动规律.
vA
对动能定理的理解及简单应用
【扩展延伸】
(1)在上题中,求小球经过最低点B时对轨道的压力大小。
(2)在上题中,若圆弧轨道粗糙,小球恰好能够经过最高点C,求此过程小球克服摩擦力所做的功。
vA
对动能定理的理解及简单应用
能优先考虑应用动能定理解答的问题
(1)物理过程中不涉及加速度、时间的问题;
(2)有多个物理过程且不需要研究整个过程中的中间状态的问题;
(3)曲线运动问题,或者变力做功的问题;
(4)含有F、l、m、v、w、Ek等物理量的力学问题.
应用动能定理解题应抓好“一过程,两状态”
“一过程”即明确研究过程,确定这一过程研究对象的受力情况和位置变化或位移信息。
“两状态”即明确研究对象的始、末状态的速度或动能情况。
动能定理在多过程问题中的应用
5. (2015·浙江理综,23)如图示,用一块长L1=1.0 m的木板在墙和桌面间架设斜面,桌子高H=0.8 m,长L2=1.5 m。斜面与水平桌面的倾角θ可在0~60°间调节后固定。将质量m=0.2 kg的小物块从斜面顶端静止释放,物块与斜面间的动摩擦因数μ1=0.05,物块与桌面间的动摩擦因数为μ2,忽略物块在斜面与桌面交接处的能量损失(重力加速度取g=10 m/s2;最大静摩擦力等于滑动摩擦力)
(1)求θ角增大到多少时,物块能从斜面开始下滑;(用正切值表示)
(2)当θ角增大到37°时,物块恰能停在桌面边缘,求物块与桌面间的动摩擦因数μ2;(已知sin 37°=0.6,cos 37°=0.8)
(3)继续增大θ角,发现θ=53°时物块落地点与墙面的距离最大,求此最大距离xm。
动能定理在多过程问题中的应用
[思考题] 某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f.轻杆向右移动不超过l时,装置可安全工作.一质量为m的小车若以速度v0撞击弹簧,将导致轻杆向右移动l/4.轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.
(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度v′和撞击速度v的关系.
审题导析
1.此时弹簧弹力等于滑动摩擦力.
2.对比两次撞击过程,小车的受力、运动、做功有哪些相同之处,哪些不同之处,遵从什么规律?
对动能定理的理解及简单应用
确定研究对象和研究过程
几个力?恒力还是变力?
运动性质及特点
运动分析
受力分析
是否做功?
正功
还是负功?
明确初、末动能
做功 情况
动能 分析
动能 定理
分阶段
或
全过程列方程
解方程
讨论
结果
牛顿运动定律
运动规律
应用动能定理的解题步骤
同课章节目录
- 第一章 怎样研究抛体运动
- 1 飞机投弹与平抛运动
- 2 研究平抛运动的规律
- 3 研究斜抛运动
- 第二章 研究圆周运动
- 1 怎样描述圆周运动
- 2 研究匀速圆周运动的规律
- 3 圆周运动的案例分析
- 4 研究离心现象及其应用
- 第三章 动能的变化与机械功
- 1 探究动能变化跟功的关系
- 2 研究功与功率
- 3 动能定理的应用
- 第四章 能量守恒与可持续发展
- 1 势能的变化与机械功
- 2 研究机械能守恒定律
- 3 能量的转化与守恒
- 4 能源与可持续发展
- 第五章 万有引力与航天
- 1 从托勒密到开普勒
- 2 万有引力定律是怎样发现的
- 3 万有引力定律与天文学的新发现
- 4 飞出地球去
- 第六章 经典力学与现代物理
- 1 经典力学的巨大成就和局限性
- 2 狭义相对论的基本原理
- 3 爱因斯坦心目中的宇宙
- 4 微观世界与量子论
