教科版(2019)高中物理 必修第一册 3.5 力的分解课件
文档属性
| 名称 | 教科版(2019)高中物理 必修第一册 3.5 力的分解课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-09 00:00:00 | ||
图片预览











文档简介
第5节 力的分解
学习目标要求
核心素养和关键能力
1.知道力的分解的概念。
2.会通过效果进行力的分解。
3.会通过正交分解法进行力的分解。
4.运用力的分解知识分析日常生活中的相关问题,培养将物理知识应用于生活和生产实践的意识。
1.科学态度与责任
将所学知识与生活相联系,尝试解决实际问题。
2.关键能力
几何法解决力的合成与分解问题。
一、力的分解
1.分力:一个力作用在物体上也可以用几个共同作用在物体上的共点力来__________,这几个力称为那一个力的分力。
2.力的分解:求__________________叫作力的分解。
3.分解法则:力的分解是力的合成的________,它也遵循________________。
4.求一个力F的分力时,如果没有限制,同一个力F可以分解为______对大小、方向不同的分力。
等效替代
一个已知力的分力
逆运算
平行四边形定则
无数
[判一判]
(1)将一个力F分解为两个力F1和F2,那么物体同时受到F1、F2和F三个力的作用。( )
(2)某个分力的大小可能大于合力。( )
(3)把一个力分解为两个分力,这两个分力共同作用的效果应当与该力作用的效果相同。( )
×
√
√
二、力的正交分解
1.定义:在许多情况下,可把一个力分解为两个__________的分力,这种分解方法称为力的正交分解。正交分解适用于各种矢量。
2.应用:例如:将力F沿x轴和y轴两个方向分解,如图所示,则Fx=________________,Fy=________________。
互相垂直
Fcos α
Fsin α
如图所示,在一根橡皮绳中间吊起一个重锤,当橡皮绳两个端点的距离慢慢变大时,橡皮绳也会慢慢变长。
■情境导入
探究
对力的分解的讨论
你能从力的分解的角度解释这个现象吗?试着通过作图的方法来分析。
答案 当端点距离变大时,两力之间的夹角变大,两个力的合力不变,则两力变大,橡皮绳被拉长(如图)。
■归纳拓展
1.无条件限制的力的分解:一个力分解为两个力,从理论上讲有无数组解。因为以同一条线段为对角线的平行四边形有无穷多个(如图甲、乙所示)。
甲 乙
由图乙知,将已知力F分解为两个等大的分力时,两分力间的夹角越大,两分力越大。
2.有条件限制的力的分解
代表合力的对角线与给定的代表分力的有向线段是否能构成平行四边形(或三角形)。若可以构成平行四边形(或三角形),说明合力可以分解成给定的分力,即有解;若不能,则无解。
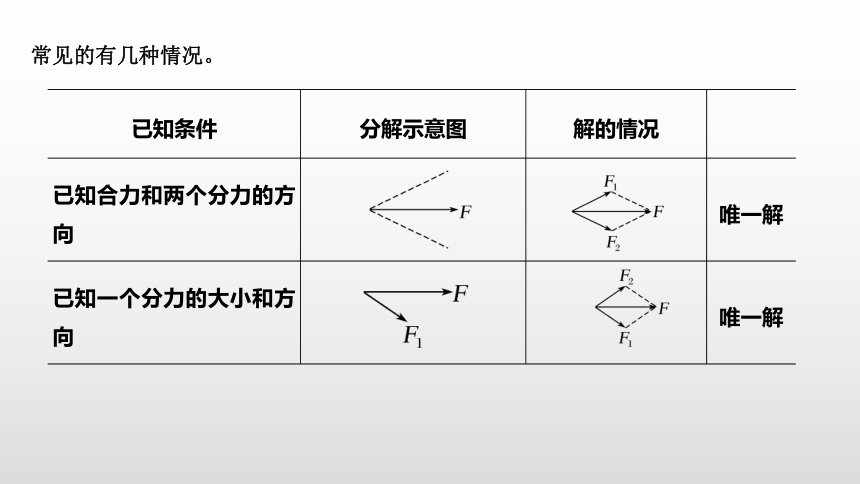
常见的有几种情况。
已知条件
分解示意图
解的情况
?
已知合力和两个分力的方向
唯一解
已知一个分力的大小和方向
唯一解
已知一个分力(F2)的大小和另一个分力(F1)的方向
①F2<Fsin θ
无解
②F2=Fsin θ
唯一解
③Fsin θ<F2<F
两解
④F2≥F
唯一解
解析 因Fsin 30°<F2<F,所以F1的大小有两种情况,如图所示,
答案 AD
[针对训练1] 按下列两种情况把一个竖直向下的180 N的力分解为两个分力。(已知sin 53°=0.8,cos 53°=0.6)
(1)一个分力水平向右,并等于240 N,求另一个分力的大小和方向;
(2)一个分力在水平方向上,另一个分力与竖直方向的夹角为30°斜向下(如图所示),求两个分力的大小。
解析 (1)力的分解如图甲所示。
甲
(2)力的分解如图乙所示。
乙
答案 (1)300 N 与竖直方向夹角为53°斜向左下
■情境导入
探究
力的效果分解法
如图所示,为了行车方便和安全,高大的桥往往有很长的引桥,在引桥上,汽车重力有什么作用效果?从力的分解的角度分析,引桥很长有什么好处?
提示 汽车重力的两个作用效果是垂直桥面向下使汽车压斜面和沿桥面向下使汽车下滑或阻碍汽车上行。高大的桥建造很长的引桥可以减小斜面的倾角,即减小汽车重力沿斜面向下的分力,使行车更安全。
■归纳拓展
1.力的分解的原则
根据力的作用效果确定分力的方向,然后再画出力的平行四边形。
2.按实际效果分解的几个实例
实例
产生效果分析
地面上物体受斜向上的拉力F,拉力F一方面使物体沿水平地面前进,另一方面向上提物体,因此拉力F可分解为水平向前的力F1和竖直向上的力F2。F1=Fcos α,F2=Fsin α
[例2] 如图所示,一个重为100 N的小球被夹在竖直的墙壁和A点之间,已知球心O与A点的连线与竖直方向成θ角,且θ=60°,所有接触点和面均不计摩擦。试求小球对墙面的压力F1和对A点的压力F2。
解析 小球的重力产生两个作用效果:使球压紧墙壁和使球压紧A点,作出重力及它的两个分力F1′和F2′构成的平行四边形,如图所示。
答案 见解析
[针对训练2] (多选)下图中按力的作用效果分解正确的是( )
解析 对B项图,物体的重力按效果分解成垂直斜面的力与垂直挡板的力,如图甲所示,故B错误;
甲 乙
对C项图,按照力的作用效果,拉力分解成如图乙所示,故C错误;A、D图中力的分解是正确的。
答案 AD
1.力的正交分解法
探究
力的正交分解法
把力沿着两个经选定的互相垂直的方向分解的方法叫力的正交分解法。在多个共点力作用下,运用正交分解法的目的是用代数运算来解决矢量的运算。在力的正交分解法中,分解的目的是求合力,尤其适用于物体受多个力的情况。
2.力的正交分解的方法和步骤
温馨提示 正交分解法的应用
(1)建立坐标系的原则:使尽量多的力落在坐标轴上,减少力的分解个数。
(2)正交分解法适用于各种矢量运算,这种方法可以将矢量运算转化为代数运算。
(3)对于运动的物体,通常两坐标轴分别沿物体运动方向和垂直物体运动方向建立。
[例3] 如图所示,重力为500 N的人通过跨过定滑轮的轻绳牵引重200 N的物体,当绳与水平面成60°角时,物体静止。不计滑轮与绳间的摩擦力。求地面对人的支持力和摩擦力。
解析 人和物体静止,所受合力皆为零。对物体受力分析可知,绳的拉力F等于物体的重力,即为200 N。
如图所示,以人为研究对象,将绳的拉力分解,
则水平方向的分力Fx=Fcos 60°=100 N
在x方向,f与Fx平衡,所以静摩擦力f=Fx=100 N,方向水平向右
在y方向,N、G、Fy平衡,故地面对人的支持力
方向竖直向上。
[针对训练3] 在同一平面内共点的四个力F1、F2、F3、F4的大小依次是19 N、40 N、30 N和15 N,方向如图所示,求这个四个力的合力。(sin 37°=0.6,cos 37°=0.8)
解析 建立如图所示直角坐标系,将力F2、F3分解到x、y轴上。
x轴上:Fx=F1+F2x-F3x=F1+F2cos 37°-F3cos 37°
=19 N+40×0.8 N-30×0.8 N=27 N
y轴上:Fy=F2y+F3y-F4=F2sin 37°+F3sin 37°-F4=40×0.6 N+30×0.6 N-15 N=27 N
学习目标要求
核心素养和关键能力
1.知道力的分解的概念。
2.会通过效果进行力的分解。
3.会通过正交分解法进行力的分解。
4.运用力的分解知识分析日常生活中的相关问题,培养将物理知识应用于生活和生产实践的意识。
1.科学态度与责任
将所学知识与生活相联系,尝试解决实际问题。
2.关键能力
几何法解决力的合成与分解问题。
一、力的分解
1.分力:一个力作用在物体上也可以用几个共同作用在物体上的共点力来__________,这几个力称为那一个力的分力。
2.力的分解:求__________________叫作力的分解。
3.分解法则:力的分解是力的合成的________,它也遵循________________。
4.求一个力F的分力时,如果没有限制,同一个力F可以分解为______对大小、方向不同的分力。
等效替代
一个已知力的分力
逆运算
平行四边形定则
无数
[判一判]
(1)将一个力F分解为两个力F1和F2,那么物体同时受到F1、F2和F三个力的作用。( )
(2)某个分力的大小可能大于合力。( )
(3)把一个力分解为两个分力,这两个分力共同作用的效果应当与该力作用的效果相同。( )
×
√
√
二、力的正交分解
1.定义:在许多情况下,可把一个力分解为两个__________的分力,这种分解方法称为力的正交分解。正交分解适用于各种矢量。
2.应用:例如:将力F沿x轴和y轴两个方向分解,如图所示,则Fx=________________,Fy=________________。
互相垂直
Fcos α
Fsin α
如图所示,在一根橡皮绳中间吊起一个重锤,当橡皮绳两个端点的距离慢慢变大时,橡皮绳也会慢慢变长。
■情境导入
探究
对力的分解的讨论
你能从力的分解的角度解释这个现象吗?试着通过作图的方法来分析。
答案 当端点距离变大时,两力之间的夹角变大,两个力的合力不变,则两力变大,橡皮绳被拉长(如图)。
■归纳拓展
1.无条件限制的力的分解:一个力分解为两个力,从理论上讲有无数组解。因为以同一条线段为对角线的平行四边形有无穷多个(如图甲、乙所示)。
甲 乙
由图乙知,将已知力F分解为两个等大的分力时,两分力间的夹角越大,两分力越大。
2.有条件限制的力的分解
代表合力的对角线与给定的代表分力的有向线段是否能构成平行四边形(或三角形)。若可以构成平行四边形(或三角形),说明合力可以分解成给定的分力,即有解;若不能,则无解。
常见的有几种情况。
已知条件
分解示意图
解的情况
?
已知合力和两个分力的方向
唯一解
已知一个分力的大小和方向
唯一解
已知一个分力(F2)的大小和另一个分力(F1)的方向
①F2<Fsin θ
无解
②F2=Fsin θ
唯一解
③Fsin θ<F2<F
两解
④F2≥F
唯一解
解析 因Fsin 30°<F2<F,所以F1的大小有两种情况,如图所示,
答案 AD
[针对训练1] 按下列两种情况把一个竖直向下的180 N的力分解为两个分力。(已知sin 53°=0.8,cos 53°=0.6)
(1)一个分力水平向右,并等于240 N,求另一个分力的大小和方向;
(2)一个分力在水平方向上,另一个分力与竖直方向的夹角为30°斜向下(如图所示),求两个分力的大小。
解析 (1)力的分解如图甲所示。
甲
(2)力的分解如图乙所示。
乙
答案 (1)300 N 与竖直方向夹角为53°斜向左下
■情境导入
探究
力的效果分解法
如图所示,为了行车方便和安全,高大的桥往往有很长的引桥,在引桥上,汽车重力有什么作用效果?从力的分解的角度分析,引桥很长有什么好处?
提示 汽车重力的两个作用效果是垂直桥面向下使汽车压斜面和沿桥面向下使汽车下滑或阻碍汽车上行。高大的桥建造很长的引桥可以减小斜面的倾角,即减小汽车重力沿斜面向下的分力,使行车更安全。
■归纳拓展
1.力的分解的原则
根据力的作用效果确定分力的方向,然后再画出力的平行四边形。
2.按实际效果分解的几个实例
实例
产生效果分析
地面上物体受斜向上的拉力F,拉力F一方面使物体沿水平地面前进,另一方面向上提物体,因此拉力F可分解为水平向前的力F1和竖直向上的力F2。F1=Fcos α,F2=Fsin α
[例2] 如图所示,一个重为100 N的小球被夹在竖直的墙壁和A点之间,已知球心O与A点的连线与竖直方向成θ角,且θ=60°,所有接触点和面均不计摩擦。试求小球对墙面的压力F1和对A点的压力F2。
解析 小球的重力产生两个作用效果:使球压紧墙壁和使球压紧A点,作出重力及它的两个分力F1′和F2′构成的平行四边形,如图所示。
答案 见解析
[针对训练2] (多选)下图中按力的作用效果分解正确的是( )
解析 对B项图,物体的重力按效果分解成垂直斜面的力与垂直挡板的力,如图甲所示,故B错误;
甲 乙
对C项图,按照力的作用效果,拉力分解成如图乙所示,故C错误;A、D图中力的分解是正确的。
答案 AD
1.力的正交分解法
探究
力的正交分解法
把力沿着两个经选定的互相垂直的方向分解的方法叫力的正交分解法。在多个共点力作用下,运用正交分解法的目的是用代数运算来解决矢量的运算。在力的正交分解法中,分解的目的是求合力,尤其适用于物体受多个力的情况。
2.力的正交分解的方法和步骤
温馨提示 正交分解法的应用
(1)建立坐标系的原则:使尽量多的力落在坐标轴上,减少力的分解个数。
(2)正交分解法适用于各种矢量运算,这种方法可以将矢量运算转化为代数运算。
(3)对于运动的物体,通常两坐标轴分别沿物体运动方向和垂直物体运动方向建立。
[例3] 如图所示,重力为500 N的人通过跨过定滑轮的轻绳牵引重200 N的物体,当绳与水平面成60°角时,物体静止。不计滑轮与绳间的摩擦力。求地面对人的支持力和摩擦力。
解析 人和物体静止,所受合力皆为零。对物体受力分析可知,绳的拉力F等于物体的重力,即为200 N。
如图所示,以人为研究对象,将绳的拉力分解,
则水平方向的分力Fx=Fcos 60°=100 N
在x方向,f与Fx平衡,所以静摩擦力f=Fx=100 N,方向水平向右
在y方向,N、G、Fy平衡,故地面对人的支持力
方向竖直向上。
[针对训练3] 在同一平面内共点的四个力F1、F2、F3、F4的大小依次是19 N、40 N、30 N和15 N,方向如图所示,求这个四个力的合力。(sin 37°=0.6,cos 37°=0.8)
解析 建立如图所示直角坐标系,将力F2、F3分解到x、y轴上。
x轴上:Fx=F1+F2x-F3x=F1+F2cos 37°-F3cos 37°
=19 N+40×0.8 N-30×0.8 N=27 N
y轴上:Fy=F2y+F3y-F4=F2sin 37°+F3sin 37°-F4=40×0.6 N+30×0.6 N-15 N=27 N
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
