教科版(2019)高中物理 必修第一册 第二章 匀变速直线运动的规律 章末核心素养提升课件
文档属性
| 名称 | 教科版(2019)高中物理 必修第一册 第二章 匀变速直线运动的规律 章末核心素养提升课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-09 19:12:30 | ||
图片预览







文档简介
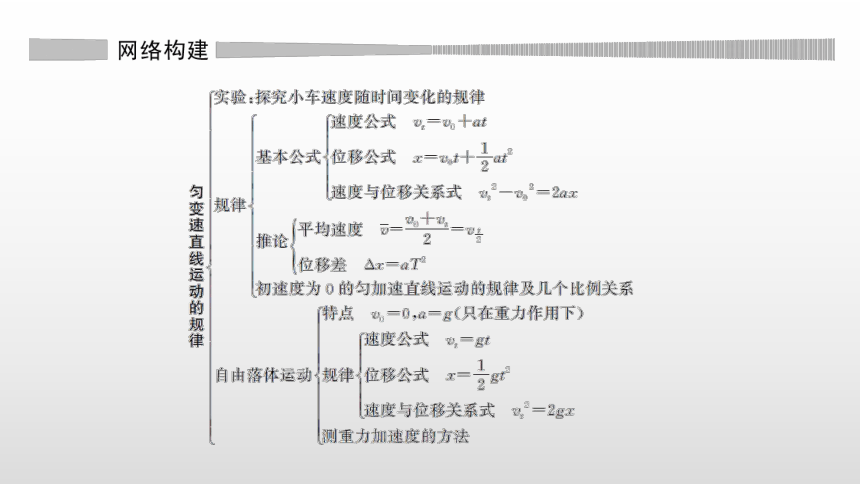
章末核心素养提升
一、逆向思维法求解运动问题
人们通常思考问题的思维反过来思考的思维方式就是逆向思维,运用逆向思维分析和解决问题的方法叫作逆向思维法。所谓逆向思维,简单来说就是“倒过来想一想。”
末速度为0的匀减速直线运动可看成初速度为0、加速度大小相等的反向匀加速直线运动。
设物体的初速度为v0,加速度大小为a,做匀减速直线运动至经过时间t速度为0,则可将此运动逆向看成初速度为0,加速度大小为a的匀加速直线运动,末速为v0,则经过的位移x可有以下表达形式:
[例1] 一跳伞员从高空离开直升机落下,开始未打开伞(如图所示),先做匀加速直线运动,落下一段距离后才打开伞,打开伞后做匀减速直线运动,加速度大小为2 m/s2,经20 s到达地面时的速度为4 m/s,试求跳伞员在空中下落的最大速度。
解析 跳伞员打开伞的一瞬间速度最大,之后一直减速到着地。用逆向思维,我们反过去看就可以认为从着地到开伞的一瞬间是做匀加速运动。规定向上为正方向,则v0=4 m/s、a=2 m/s2、t=20 s,把这些数据代入公式vt=v0+at有vt=4 m/s+2×20 m/s=44 m/s。则跳伞员在空中下落的最大速度为44 m/s,方向向下。
答案 44 m/s,方向向下
[针对训练1] 一小球以某一初速度沿光滑斜面匀减速上滑,到达顶端时速度为0,历时3 s,位移为9 m,求其第1 s内的位移。
解析 反过来看,小球做初速度为0的匀加速直线运动,
t2=3 s内的位移x2=9 m,
解得小球沿斜面上滑在第1 s内的位移为
x=x2-x1=5 m。
答案 5 m
二、测定重力加速度的方法
1.实验设计
利用频闪照片,或利用打点计时器能够把做自由落体运动的物体的位置和相应的时刻记录下来。根据对匀变速直线运动的研究,测量物体下落的加速度,进而研究自由落体运动是否是匀加速直线运动,以证实猜想。
2.实验方法
(1)打点计时器法
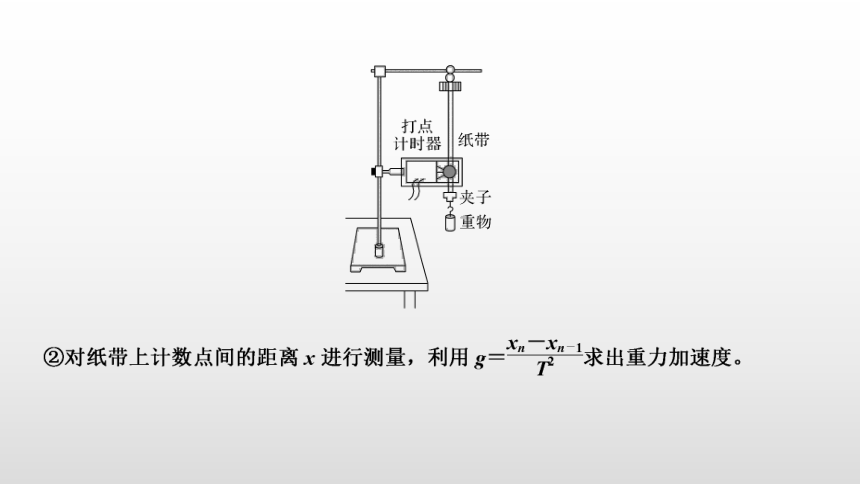
①实验装置如图所示。打点计时器固定在铁架台上,纸带一端系着重物,另一端穿过计时器。用夹子夹住纸带,启动计时器,松开夹子后重物自由下落,计时器在纸带上留下一串小点。
特别提醒 (1)为尽量减小空气阻力的影响,重物应选密度大的,如铁锤等。
(2)打点计时器应竖直固定好。
(3)重物应靠近打点计时器释放,且要先打开打点计时器的电源再放开重物。
(4)改变重物的质量,重复打出几条纸带。
(5)选点迹清晰,且1、2两点间距离小于或接近2 mm的纸带分析探究。
(3)滴水法
①如图所示,让水滴自水龙头滴下,在水龙头正下方放一个盘,调节水龙头,让水一滴一滴地滴下,并调节使第一滴水碰到盘的瞬间,第二滴水正好从水龙头开始下落,并且能依次持续下去。
特别提醒 (1)打点计时器法的误差主要来自阻力的影响和测量误差。
(2)频闪照相法和滴水法的误差主要是测量误差。
[例2] 下图中甲、乙两图都是使用电磁打点计时器测量重力加速度g的装置示意图,已知该打点计时器的打点频率为50 Hz。
(1)甲、乙两图相比较,图______所示的装置更合理。
(2)丙图是采用较合理的装置并按正确的实验步骤进行实验打出的一条纸带,其中打出的第一个点标为1,后面依次打下的一系列点迹分别标为2、3、4、5…经测量,第15至第17点间的距离为11.70 cm第1至第16点间距离为43.88 cm,则打下第16个点时,重锤下落的速度大小为________m/s,测出的重力加速度值为g=______m/s2。(要求保留3位有效数字)
解析 (1)甲图释放时更稳定,既能更有效地减小摩擦力,又能保证释放时初速度的大小为零,所以甲图更合理。
答案 (1)甲 (2)2.93 9.78(±0.02均可)
[针对训练2] 如图所示,在频闪照相中得到的一张真空中羽毛与苹果自由下落的局部频闪照片。已知频闪仪每隔时间t闪光一次。关于提供的信息及相关数据处理,下列说法正确的是( )
答案 D
[针对训练3] 滴水法测重力加速度的过程是这样的:让水龙头的水一滴一滴地滴在其正下方的盘子里,调整水龙头,让前一滴水滴到盘子而听到声音时,后一滴水恰好离开水龙头。从第1次听到水击盘声时开始计时,测出n次听到水击盘声的总时间为t,用刻度尺量出水龙头到盘子的高度差为h,即可算出重力加速度。设人耳能区别两个声音的时间间隔为0.1 s,声速为340 m/s。g取10 m/s2,则( )
答案 D
三、匀变速直线运动问题的分析技巧
分析匀变速直线运动的技巧:“一画、二选、三注意”
一画:根据题意画出物体运动 ,使运动过程直观清晰。
运动过程图,在图中标明已知量、待求量
示意图
二选:从以下常用方法中选取合适的方法
三注意:注意列运动学方程时,方程式中每一个物理量均对应同一运动过程。
法2 比例法
对于初速度为零的匀变速直线运动,在连续相等的时间里通过的位移之比为
x1∶x2∶x3∶…∶xn=1∶3∶5∶…∶(2n-1)。
通过xAB的时间为t,故通过xBC的时间tBC=t。
法3 中间时刻速度法
利用推论:中间时刻的瞬时速度等于这段位移的平均速度,
可以看出vB正好等于AC段的平均速度,因此B点是中间时刻的位置,因此有tBC=t。
法4 图像法
利用相似三角形面积之比等于对应边平方比的方法,作出v-t图像,如图所示,
答案 t
A.a1<a2 B.a1=a2 C.a1>a2 D.条件不足,无法确定
答案 A
四、匀变速直线运动的比例式
1.初速度为零的匀加速直线运动,按时间等分(设相等的时间间隔为T)
2.初速度为零的匀加速直线运动,按位移等分(设相等的位移为x0)
温馨提示 (1)比例式解题适用初速度为零的匀加速直线运动。
(2)对末速度为零的匀减速直线运动,可逆向分析应用比例关系解答。
[例4] 物体从静止开始做匀加速直线运动,加速度为1 m/s2,求:
(1)物体在2 s内的位移;
(2)物体在第2 s内的位移;
(3)物体在第二个2 s内的位移。
(3)以2 s为一个时间单位,设物体在第二个2 s内的位移为x′,由x2∶x′=1∶3得
x′=3x2=3×2 m=6 m。
答案 (1)2 m (2)1.5 m (3)6 m
[针对训练5] 在冰壶世锦赛上中国女子冰壶队夺得世界冠军,如图所示,一冰壶以速度v垂直进入两个相同的矩形区域做匀减速运动,且刚要离开第二个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是多少?(冰壶可看成质点)
答案 见解析
一、逆向思维法求解运动问题
人们通常思考问题的思维反过来思考的思维方式就是逆向思维,运用逆向思维分析和解决问题的方法叫作逆向思维法。所谓逆向思维,简单来说就是“倒过来想一想。”
末速度为0的匀减速直线运动可看成初速度为0、加速度大小相等的反向匀加速直线运动。
设物体的初速度为v0,加速度大小为a,做匀减速直线运动至经过时间t速度为0,则可将此运动逆向看成初速度为0,加速度大小为a的匀加速直线运动,末速为v0,则经过的位移x可有以下表达形式:
[例1] 一跳伞员从高空离开直升机落下,开始未打开伞(如图所示),先做匀加速直线运动,落下一段距离后才打开伞,打开伞后做匀减速直线运动,加速度大小为2 m/s2,经20 s到达地面时的速度为4 m/s,试求跳伞员在空中下落的最大速度。
解析 跳伞员打开伞的一瞬间速度最大,之后一直减速到着地。用逆向思维,我们反过去看就可以认为从着地到开伞的一瞬间是做匀加速运动。规定向上为正方向,则v0=4 m/s、a=2 m/s2、t=20 s,把这些数据代入公式vt=v0+at有vt=4 m/s+2×20 m/s=44 m/s。则跳伞员在空中下落的最大速度为44 m/s,方向向下。
答案 44 m/s,方向向下
[针对训练1] 一小球以某一初速度沿光滑斜面匀减速上滑,到达顶端时速度为0,历时3 s,位移为9 m,求其第1 s内的位移。
解析 反过来看,小球做初速度为0的匀加速直线运动,
t2=3 s内的位移x2=9 m,
解得小球沿斜面上滑在第1 s内的位移为
x=x2-x1=5 m。
答案 5 m
二、测定重力加速度的方法
1.实验设计
利用频闪照片,或利用打点计时器能够把做自由落体运动的物体的位置和相应的时刻记录下来。根据对匀变速直线运动的研究,测量物体下落的加速度,进而研究自由落体运动是否是匀加速直线运动,以证实猜想。
2.实验方法
(1)打点计时器法
①实验装置如图所示。打点计时器固定在铁架台上,纸带一端系着重物,另一端穿过计时器。用夹子夹住纸带,启动计时器,松开夹子后重物自由下落,计时器在纸带上留下一串小点。
特别提醒 (1)为尽量减小空气阻力的影响,重物应选密度大的,如铁锤等。
(2)打点计时器应竖直固定好。
(3)重物应靠近打点计时器释放,且要先打开打点计时器的电源再放开重物。
(4)改变重物的质量,重复打出几条纸带。
(5)选点迹清晰,且1、2两点间距离小于或接近2 mm的纸带分析探究。
(3)滴水法
①如图所示,让水滴自水龙头滴下,在水龙头正下方放一个盘,调节水龙头,让水一滴一滴地滴下,并调节使第一滴水碰到盘的瞬间,第二滴水正好从水龙头开始下落,并且能依次持续下去。
特别提醒 (1)打点计时器法的误差主要来自阻力的影响和测量误差。
(2)频闪照相法和滴水法的误差主要是测量误差。
[例2] 下图中甲、乙两图都是使用电磁打点计时器测量重力加速度g的装置示意图,已知该打点计时器的打点频率为50 Hz。
(1)甲、乙两图相比较,图______所示的装置更合理。
(2)丙图是采用较合理的装置并按正确的实验步骤进行实验打出的一条纸带,其中打出的第一个点标为1,后面依次打下的一系列点迹分别标为2、3、4、5…经测量,第15至第17点间的距离为11.70 cm第1至第16点间距离为43.88 cm,则打下第16个点时,重锤下落的速度大小为________m/s,测出的重力加速度值为g=______m/s2。(要求保留3位有效数字)
解析 (1)甲图释放时更稳定,既能更有效地减小摩擦力,又能保证释放时初速度的大小为零,所以甲图更合理。
答案 (1)甲 (2)2.93 9.78(±0.02均可)
[针对训练2] 如图所示,在频闪照相中得到的一张真空中羽毛与苹果自由下落的局部频闪照片。已知频闪仪每隔时间t闪光一次。关于提供的信息及相关数据处理,下列说法正确的是( )
答案 D
[针对训练3] 滴水法测重力加速度的过程是这样的:让水龙头的水一滴一滴地滴在其正下方的盘子里,调整水龙头,让前一滴水滴到盘子而听到声音时,后一滴水恰好离开水龙头。从第1次听到水击盘声时开始计时,测出n次听到水击盘声的总时间为t,用刻度尺量出水龙头到盘子的高度差为h,即可算出重力加速度。设人耳能区别两个声音的时间间隔为0.1 s,声速为340 m/s。g取10 m/s2,则( )
答案 D
三、匀变速直线运动问题的分析技巧
分析匀变速直线运动的技巧:“一画、二选、三注意”
一画:根据题意画出物体运动 ,使运动过程直观清晰。
运动过程图,在图中标明已知量、待求量
示意图
二选:从以下常用方法中选取合适的方法
三注意:注意列运动学方程时,方程式中每一个物理量均对应同一运动过程。
法2 比例法
对于初速度为零的匀变速直线运动,在连续相等的时间里通过的位移之比为
x1∶x2∶x3∶…∶xn=1∶3∶5∶…∶(2n-1)。
通过xAB的时间为t,故通过xBC的时间tBC=t。
法3 中间时刻速度法
利用推论:中间时刻的瞬时速度等于这段位移的平均速度,
可以看出vB正好等于AC段的平均速度,因此B点是中间时刻的位置,因此有tBC=t。
法4 图像法
利用相似三角形面积之比等于对应边平方比的方法,作出v-t图像,如图所示,
答案 t
A.a1<a2 B.a1=a2 C.a1>a2 D.条件不足,无法确定
答案 A
四、匀变速直线运动的比例式
1.初速度为零的匀加速直线运动,按时间等分(设相等的时间间隔为T)
2.初速度为零的匀加速直线运动,按位移等分(设相等的位移为x0)
温馨提示 (1)比例式解题适用初速度为零的匀加速直线运动。
(2)对末速度为零的匀减速直线运动,可逆向分析应用比例关系解答。
[例4] 物体从静止开始做匀加速直线运动,加速度为1 m/s2,求:
(1)物体在2 s内的位移;
(2)物体在第2 s内的位移;
(3)物体在第二个2 s内的位移。
(3)以2 s为一个时间单位,设物体在第二个2 s内的位移为x′,由x2∶x′=1∶3得
x′=3x2=3×2 m=6 m。
答案 (1)2 m (2)1.5 m (3)6 m
[针对训练5] 在冰壶世锦赛上中国女子冰壶队夺得世界冠军,如图所示,一冰壶以速度v垂直进入两个相同的矩形区域做匀减速运动,且刚要离开第二个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是多少?(冰壶可看成质点)
答案 见解析
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
