教科版(2019)高中物理 必修第一册 专题拓展课二 运动图像与追及相遇问题课件
文档属性
| 名称 | 教科版(2019)高中物理 必修第一册 专题拓展课二 运动图像与追及相遇问题课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-09 19:36:20 | ||
图片预览








文档简介
专题拓展课二 运动图像与追及相遇问题
学习目标要求
1.知道一般直线运动和匀变速直线运动的x-t图像和v-t图像中坐标、斜率、截距、交点的含义,能根据图像分析加速度、位移等量及物体的运动。
2.掌握追及相遇问题的分析思路和方法。
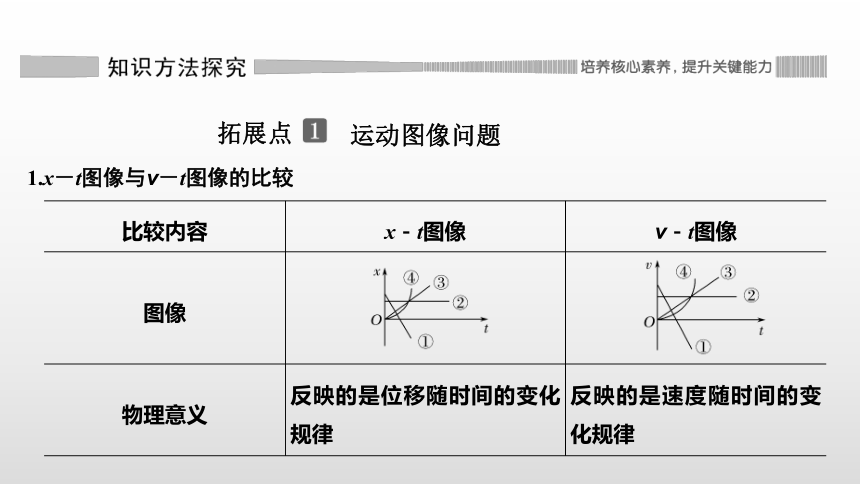
1.x-t图像与v-t图像的比较
拓展点
运动图像问题
比较内容
x-t图像
v-t图像
图像
物理意义
反映的是位移随时间的变化规律
反映的是速度随时间的变化规律
物体的运动性质
①
表示物体从位移为正处开始一直做反向匀速直线运动并过零位移处
表示物体先做正向匀减速直线运动,再做负向匀加速直线运动
②
表示物体静止不动
表示物体做正向匀速直线运动
③
表示物体从位移为零处开始做正向匀速运动
表示物体从静止开始做正向匀加速直线运动
④
表示物体做加速直线运动
表示物体做加速度逐渐增大的加速运动
图像与坐标轴围成的“面积”的意义
无实际意义
表示相应时间内的位移
2.x-t图像的应用
(1)根据图像斜率可以求出物体的速度。
(2)由图像判断物体运动的方向。
(3)根据图像可以求出一段时间内的位移或发生一段位移所用的时间。
(4)在同一坐标系中若画出几个物体的位移图像,可比较它们运动的快慢,也可知道它们相遇(两图线的交点)的时刻。
3.v-t图像的应用
(1)由图像判断物体运动的方向。
(2)根据图像的斜率可以求出物体的加速度。
(3)根据图像可以求出某一时刻的速度或某段时间内速度的变化量。
(4)根据图线与t轴所围图形面积求物体的位移。
(5)根据图像可以判断物体的运动性质。
(6)在同一坐标系中,若画出几个物体的速度图像,可比较它们速度变化的快慢,也可知道它们速度相等(两图线的交点)的时刻。
[例1] (多选)物体甲的x-t图像和物体乙的v-t图像如图所示,则这两物体的运动情况是( )
A.甲在整个t=6 s时间内运动方向一直不变,它通过的总位移大小为4 m
B.甲在整个t=6 s时间内有往返运动,它通过的总位移为零
C.乙在整个t=6 s时间内有往返运动,它通过的总位移为零
D.乙在整个t=6 s时间内运动方向一直不变,它通过的总位移大小为4 m
解析 甲图为x-t图像,图像的斜率表示速度,甲的斜率一直为正,故甲的运动方向不变,通过的总位移大小为4 m,A正确,B错误;乙图为v-t图像,速度有正负,表示有往返运动。v-t图像中图线与时间轴所围面积表示位移的大小,在整个t=6 s时间内乙通过的总位移为零,C正确,D错误。
答案 AC
[变式训练1] (多选)质点做直线运动的v-t图像如图所示,规定向右为正方向,则该质点在前8 s 内的平均速度及质点运动的总路程为( )
A.总路程为2 m
B.平均速度为0.25 m/s,方向向左
C.总路程为8 m
D.平均速度为1 m/s,方向向左
答案 BC
1.追及相遇问题
两物体在同一直线上一前一后运动,它们之间的距离发生变化时,可能出现最大距离、最小距离或者距离为零的情况,这类问题称为追及相遇问题,讨论追及相遇问题的实质是两物体能否在同一时刻到达同一位置。
拓展点
追及相遇问题
2.分析追及相遇问题的思路和方法
(1)抓住一个条件、用好两个关系
①一个条件:速度相等。这是两物体是否追上(或相撞)、距离最大、距离最小的临界点,是解题的切入点。
②两个关系:时间关系和位移关系。通过画示意图找出两物体位移之间的数量关系,是解题的突破口。
(2)常用方法
①物理分析法:抓住“两物体能否同时到达空间某位置”这一关键,认真审题,挖掘题中的隐含条件,建立物体运动关系的图景,并画出运动情况示意图,找出位移关系。
②图像法:将两者的v-t图像画在同一坐标系中,然后利用图像求解。
③数学分析法:设从开始至相遇时间为t,根据条件列位移关系方程,得到关于t的一元二次方程,用判别式进行讨论,若Δ>0,即有两个解,说明可以相遇两次,若Δ=0,说明刚好追上或相遇;若Δ<0,说明追不上或不能相碰。
[例2] 一辆汽车以3 m/s2的加速度开始启动的瞬间,一辆以6 m/s的速度做匀速直线运动的自行车恰好从汽车的旁边通过。试求:
(1)汽车在追上自行车前运动多长时间与自行车相距最远?此时的距离是多少?
(2)汽车经多长时间追上自行车?追上自行车时汽车的瞬时速度是多大?
解析 (1)法1 基本规律法
汽车与自行车的速度相等时两车相距最远,设此时经过的时间为t1,汽车的速度为v1,两车间的距离为Δx,则有v1=at1=v自
法2 极值法或数学分析法
设汽车在追上自行车之前经过时间t1,两车间的距离为
由二次函数求极值的条件知t1=2 s时,Δx最大
代入得Δx=6 m
法3 图像法
自行车和汽车运动的v-t图像如图所示,由图可以看出,在相遇前,t1时刻两车速度相等,两车相距最远,此时的距离为阴影三角形的面积。
(2)法1 基本规律法
当两车位移相等时,汽车追上自行车,设此时经过的时间为t2,汽车的瞬时速度为v2,则有
答案 (1)2 s 6 m (2)4 s 12 m/s
法2 图像法
由图可以看出,在t1时刻前后,标有阴影的两个三角形面积相等,此时汽车与自行车的位移相等,即汽车与自行车相遇。由几何关系知t2=2t1=4 s,v2=at2=3×4 m/s=12 m/s。
[变式训练2] 平直公路上有甲、乙两辆汽车,甲以0.5 m/s2的加速度由静止开始行驶,乙在甲的前方200 m处以5 m/s 的速度做同方向的匀速运动,问:
(1)甲何时追上乙?甲追上乙时的速度为多大?此时甲离出发点多远?
(2)在追赶过程中,甲、乙之间何时有最大距离?这个距离为多少?
解析 画出示意图,如图所示,
甲追上乙时,x甲=x0+x乙,且t甲=t乙,根据匀变速直线运动、匀速直线运动的位移公式列出方程,即能解得正确的结果。
这时甲的速度v甲=a甲t=0.5×40 m/s=20 m/s。
(2)在追赶过程中当v甲=v乙时,甲、乙之间的距离达到最大值。
由a甲t′=v乙,得t′=10 s。
答案 (1)40 s 20 m/s 400 m (2)10 s末有最大距离 225 m
学习目标要求
1.知道一般直线运动和匀变速直线运动的x-t图像和v-t图像中坐标、斜率、截距、交点的含义,能根据图像分析加速度、位移等量及物体的运动。
2.掌握追及相遇问题的分析思路和方法。
1.x-t图像与v-t图像的比较
拓展点
运动图像问题
比较内容
x-t图像
v-t图像
图像
物理意义
反映的是位移随时间的变化规律
反映的是速度随时间的变化规律
物体的运动性质
①
表示物体从位移为正处开始一直做反向匀速直线运动并过零位移处
表示物体先做正向匀减速直线运动,再做负向匀加速直线运动
②
表示物体静止不动
表示物体做正向匀速直线运动
③
表示物体从位移为零处开始做正向匀速运动
表示物体从静止开始做正向匀加速直线运动
④
表示物体做加速直线运动
表示物体做加速度逐渐增大的加速运动
图像与坐标轴围成的“面积”的意义
无实际意义
表示相应时间内的位移
2.x-t图像的应用
(1)根据图像斜率可以求出物体的速度。
(2)由图像判断物体运动的方向。
(3)根据图像可以求出一段时间内的位移或发生一段位移所用的时间。
(4)在同一坐标系中若画出几个物体的位移图像,可比较它们运动的快慢,也可知道它们相遇(两图线的交点)的时刻。
3.v-t图像的应用
(1)由图像判断物体运动的方向。
(2)根据图像的斜率可以求出物体的加速度。
(3)根据图像可以求出某一时刻的速度或某段时间内速度的变化量。
(4)根据图线与t轴所围图形面积求物体的位移。
(5)根据图像可以判断物体的运动性质。
(6)在同一坐标系中,若画出几个物体的速度图像,可比较它们速度变化的快慢,也可知道它们速度相等(两图线的交点)的时刻。
[例1] (多选)物体甲的x-t图像和物体乙的v-t图像如图所示,则这两物体的运动情况是( )
A.甲在整个t=6 s时间内运动方向一直不变,它通过的总位移大小为4 m
B.甲在整个t=6 s时间内有往返运动,它通过的总位移为零
C.乙在整个t=6 s时间内有往返运动,它通过的总位移为零
D.乙在整个t=6 s时间内运动方向一直不变,它通过的总位移大小为4 m
解析 甲图为x-t图像,图像的斜率表示速度,甲的斜率一直为正,故甲的运动方向不变,通过的总位移大小为4 m,A正确,B错误;乙图为v-t图像,速度有正负,表示有往返运动。v-t图像中图线与时间轴所围面积表示位移的大小,在整个t=6 s时间内乙通过的总位移为零,C正确,D错误。
答案 AC
[变式训练1] (多选)质点做直线运动的v-t图像如图所示,规定向右为正方向,则该质点在前8 s 内的平均速度及质点运动的总路程为( )
A.总路程为2 m
B.平均速度为0.25 m/s,方向向左
C.总路程为8 m
D.平均速度为1 m/s,方向向左
答案 BC
1.追及相遇问题
两物体在同一直线上一前一后运动,它们之间的距离发生变化时,可能出现最大距离、最小距离或者距离为零的情况,这类问题称为追及相遇问题,讨论追及相遇问题的实质是两物体能否在同一时刻到达同一位置。
拓展点
追及相遇问题
2.分析追及相遇问题的思路和方法
(1)抓住一个条件、用好两个关系
①一个条件:速度相等。这是两物体是否追上(或相撞)、距离最大、距离最小的临界点,是解题的切入点。
②两个关系:时间关系和位移关系。通过画示意图找出两物体位移之间的数量关系,是解题的突破口。
(2)常用方法
①物理分析法:抓住“两物体能否同时到达空间某位置”这一关键,认真审题,挖掘题中的隐含条件,建立物体运动关系的图景,并画出运动情况示意图,找出位移关系。
②图像法:将两者的v-t图像画在同一坐标系中,然后利用图像求解。
③数学分析法:设从开始至相遇时间为t,根据条件列位移关系方程,得到关于t的一元二次方程,用判别式进行讨论,若Δ>0,即有两个解,说明可以相遇两次,若Δ=0,说明刚好追上或相遇;若Δ<0,说明追不上或不能相碰。
[例2] 一辆汽车以3 m/s2的加速度开始启动的瞬间,一辆以6 m/s的速度做匀速直线运动的自行车恰好从汽车的旁边通过。试求:
(1)汽车在追上自行车前运动多长时间与自行车相距最远?此时的距离是多少?
(2)汽车经多长时间追上自行车?追上自行车时汽车的瞬时速度是多大?
解析 (1)法1 基本规律法
汽车与自行车的速度相等时两车相距最远,设此时经过的时间为t1,汽车的速度为v1,两车间的距离为Δx,则有v1=at1=v自
法2 极值法或数学分析法
设汽车在追上自行车之前经过时间t1,两车间的距离为
由二次函数求极值的条件知t1=2 s时,Δx最大
代入得Δx=6 m
法3 图像法
自行车和汽车运动的v-t图像如图所示,由图可以看出,在相遇前,t1时刻两车速度相等,两车相距最远,此时的距离为阴影三角形的面积。
(2)法1 基本规律法
当两车位移相等时,汽车追上自行车,设此时经过的时间为t2,汽车的瞬时速度为v2,则有
答案 (1)2 s 6 m (2)4 s 12 m/s
法2 图像法
由图可以看出,在t1时刻前后,标有阴影的两个三角形面积相等,此时汽车与自行车的位移相等,即汽车与自行车相遇。由几何关系知t2=2t1=4 s,v2=at2=3×4 m/s=12 m/s。
[变式训练2] 平直公路上有甲、乙两辆汽车,甲以0.5 m/s2的加速度由静止开始行驶,乙在甲的前方200 m处以5 m/s 的速度做同方向的匀速运动,问:
(1)甲何时追上乙?甲追上乙时的速度为多大?此时甲离出发点多远?
(2)在追赶过程中,甲、乙之间何时有最大距离?这个距离为多少?
解析 画出示意图,如图所示,
甲追上乙时,x甲=x0+x乙,且t甲=t乙,根据匀变速直线运动、匀速直线运动的位移公式列出方程,即能解得正确的结果。
这时甲的速度v甲=a甲t=0.5×40 m/s=20 m/s。
(2)在追赶过程中当v甲=v乙时,甲、乙之间的距离达到最大值。
由a甲t′=v乙,得t′=10 s。
答案 (1)40 s 20 m/s 400 m (2)10 s末有最大距离 225 m
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
