教科版(2019)高中物理 必修第一册 2.3 匀变速直线运动位移与时间的关系课件
文档属性
| 名称 | 教科版(2019)高中物理 必修第一册 2.3 匀变速直线运动位移与时间的关系课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-09 19:46:45 | ||
图片预览










文档简介
第3节 匀变速直线运动位移与时间的关系
学习目标要求
核心素养和关键能力
1.知道匀速直线运动的位移与v-t图像中矩形面积的对应关系。
2.理解匀变速直线运动的位移与时间的关系式,会应用此关系式分析和计算有关匀变速直线运动问题。
3.了解利用极限思想推导位移公式的方法。
4.理解匀变速直线运动的速度与位移的关系。
5.会应用速度与位移的关系式分析有关问题。
1.科学探究
用科学研究中的极限方法分析物理问题,通过推理,获得结论。
2.关键能力
利用数学思维来研究物理问题的能力。
一、匀速直线运动的位移
1.位移公式:x=______。
2.v-t图像如图所示
3.v-t图像特点
(1)平行于________的直线。
(2)位移在数值上等于v-t图线与对应的时间轴所包围的矩形的______。
vt
时间轴
面积
[想一想]
v-t图像中,图线与时间轴所围成图形的面积与位移有何关系?
提示 v-t图像的图线在时间轴上方表明物体向正方向运动,图线与时间轴所围的矩形的面积代表物体的位移为正值;图线与时间轴所围的面积在时间轴的下方表明物体的位移是负值。
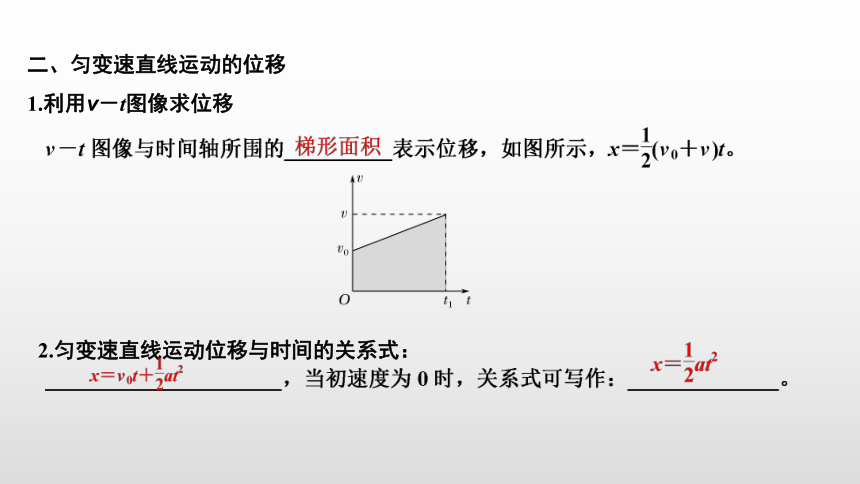
二、匀变速直线运动的位移
1.利用v-t图像求位移
2.匀变速直线运动位移与时间的关系式:
[判一判]
(1)物体运动的初速度越大,位移越大。( )
(2)物体运动的加速度越大,位移越大。( )
(3)物体做匀加速直线运动时,a取正值。( )
×
×
×
如图所示
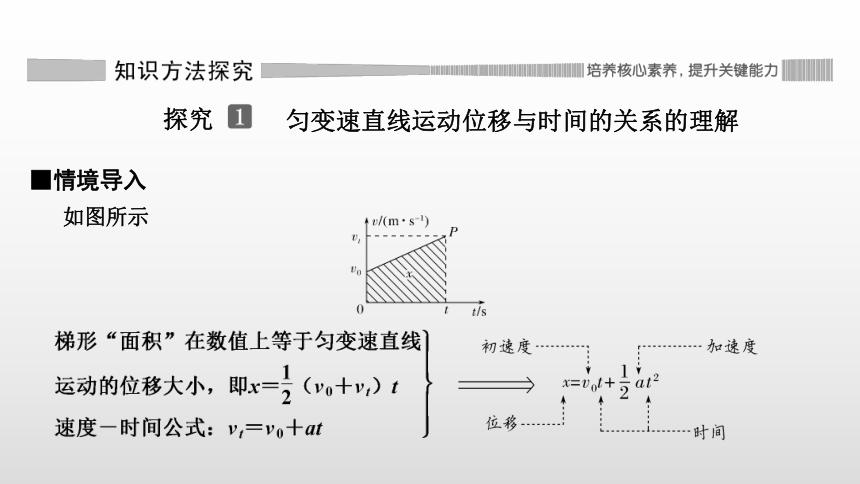
■情境导入
探究
匀变速直线运动位移与时间的关系的理解
■归纳拓展
某质点做匀变速直线运动,已知初速度为v0,在t时刻的速度为v,加速度为a。其v-t图像如图所示。
(1)把匀变速直线运动的v-t图像分成几个小段,如图所示。每段位移≈每段起始时刻速度×每段的时间=对应矩形的面积。故整个过程的位移≈各个小矩形的面积之和。
(2)把运动过程分为更多的小段,如图所示,各小矩形的面积之和可以更精确地表示物体在整个过程的位移。
(3)把整个运动过程分得非常细,很多小矩形合在一起形成了一个梯形OABC,梯形面积就代表物体在相应时间间隔内的位移。
如图所示,速度图线和时间轴所包围的梯形面积为
[例1] 一物体做匀减速直线运动,初速度大小为v0=5 m/s,加速度大小为a=0.5 m/s2,求:
(1)物体在前3 s内的位移;
(2)物体在第3 s内的位移;
(3)物体在15 s内的位移。
因此,第3 s内的位移Δx=x3-x2=12.75 m-9 m=3.75 m。
(3)物体匀减速运动到速度为零时所用时间
答案 (1)12.75 m (2)3.75 m (3)25 m
[针对训练1] 2019年12月8日,观众在“冰立方”观看中国青少年冰壶公开赛女子冰壶决赛,如图甲所示。比赛为期6天,男女各10支青少年队伍在“奥运标准”的全新冰面上展开激烈角逐,最终日本札幌队获得男子组第一名,吉林省队获得女子组第一名。如图乙所示,冰壶以速度v垂直进入四个矩形区域沿虚线做匀减速直线运动,且刚要离开第四个矩形区域边缘的E点时,速度恰好为零。冰壶通过前三个矩形的时间为t,试通过所学知识计算冰壶通过四个矩形区域所需的时间。
甲 乙
解析 从A到E的时间为t1,设每个矩形区域的长为l。
答案 2t
探究
匀变速直线运动推论——平均速度
[例2] 一滑雪运动员从85 m长的山坡上匀加速滑下,初速度是1.8 m/s,末速度是5.0 m/s。
求:(1)滑雪运动员通过这段斜坡需要多长时间?
(2)滑雪运动员通过斜坡中间时刻的瞬时速度是多少?
解析 (1)法一 利用速度公式和位移公式求解。
可得a=0.128 m/s2
t=25 s。
法二 利用平均速度公式求解。
答案 (1)25 s (2)3.4 m/s
[针对训练2] 一辆汽车4 s内做匀加速直线运动,初速度为2 m/s,末速度为10 m/s,在这段时间内,下列说法正确的是( )
A.汽车的加速度为4 m/s2
B.汽车的加速度为3 m/s2
C.汽车的位移为24 m
D.汽车的平均速度为3 m/s
答案 C
探究
匀变速直线运动推论——逐差相等
3.应用
[例3] 从斜面上某一位置每隔0.1 s释放一个相同的小球,释放后小球做匀加速直线运动,在连续释放几个后,对在斜面上滚动的小球拍下如图所示的照片,测得xAB=15 cm,xBC=20 cm。试求:
(1)小球的加速度是多少?
(2)拍摄时小球B的速度是多少?
(3)拍摄时xCD是多少?
解析 小球释放后做匀加速直线运动,且每相邻的两个小球的时间间隔相等,均为0.1 s,可以认为A、B、C、D各点是一个小球在不同时刻的位置。
即xCD=2xBC-xAB=2×20×10-2 m-15×10-2 m=25×10-2 m=0.25 m。
答案 (1)5 m/s2 (2)1.75 m/s (3)0.25 m
[针对训练3] 一个向正东方向做匀变速直线运动的物体,在第3 s内发生的位移为8 m,在第5 s内发生的位移为5 m,则关于物体运动加速度的描述正确的是 ( )
A.大小为3 m/s2,方向为正东方向
B.大小为3 m/s2,方向为正西方向
C.大小为1.5 m/s2,方向为正东方向
D.大小为1.5 m/s2,方向为正西方向
解析 设第3 s内、第5 s内位移分别为x3、x5,则x5-x3=x5-x4+x4-x3=2aT2,得a=-1.5 m/s2,负号表示方向沿正西。故选项D正确。
答案 D
探究
根据v-t图像求物体的位移
[例4] 某一做直线运动的物体的图像如图所示,根据图像求:
(1)物体距出发点的最远距离;
(2)前4 s内物体的位移;
(3)前4 s内物体通过的路程。
答案 (1)6 m (2)5 m (3)7 m
[针对训练4] 一质点的v-t图像如图所示,求它在前2 s内和前4 s内的位移。
解析 位移大小等于图线与时间轴t所围成的面积
所以质点在前4 s内的位移
x=x1+x2=5 m-5 m=0。
答案 5 m 0
科学思维之科学推理
【题目示例】
在匀速直线运动中,物体运动的速度不变,因此位移x=vt,这在数值上恰好等于v-t图像中阴影部分的面积,如图甲所示。证明:在初速度为v0、加速度为a的匀变速度直线运动中,如图乙,梯形的面积在数值上等于匀变速直线运动的位移大小;并推导出位移公式(用v0、a、t表示)。
【推理思维】 在匀变速直线运动中,虽然速度时刻变化,但只要时间足够小,速度的变化就非常小,在这段时间内就可以近似地应用匀速直线运动的公式来计算位移,如图甲所示;如果我们把每一小段Δt内的运动看作匀速运动,则矩形面积之和等于各段匀速直线运动的位移之和,显然小于匀变速直线运动在该时间内的位移,但所取时间段Δt越小,各匀速直线运动位移之和与匀变速直线运动位移之间的差值就越小,如图乙所示,当Δt→0时,各矩形面积之和趋近于v-t图线下面的面积,可以想象,如果把整个运动过程划分得非常细,很多小矩形的面积之和就能准确代表物体的位移了,位移的大小就等于图丙所示的梯形面积。
【推理过程】
解析 匀变速直线运动,物体的位移对应v-t图线和时间轴所包围的图像的“面积”。
答案 见解析
【题后感悟】 对于匀变速直线运动位移公式的推理,运用了“无限分割,逐步逼近”的微分思想,在今后学习重力做功与路径的关系中还会用到。此推理方法实质上是微积分思想在高中物理的体现。
学习目标要求
核心素养和关键能力
1.知道匀速直线运动的位移与v-t图像中矩形面积的对应关系。
2.理解匀变速直线运动的位移与时间的关系式,会应用此关系式分析和计算有关匀变速直线运动问题。
3.了解利用极限思想推导位移公式的方法。
4.理解匀变速直线运动的速度与位移的关系。
5.会应用速度与位移的关系式分析有关问题。
1.科学探究
用科学研究中的极限方法分析物理问题,通过推理,获得结论。
2.关键能力
利用数学思维来研究物理问题的能力。
一、匀速直线运动的位移
1.位移公式:x=______。
2.v-t图像如图所示
3.v-t图像特点
(1)平行于________的直线。
(2)位移在数值上等于v-t图线与对应的时间轴所包围的矩形的______。
vt
时间轴
面积
[想一想]
v-t图像中,图线与时间轴所围成图形的面积与位移有何关系?
提示 v-t图像的图线在时间轴上方表明物体向正方向运动,图线与时间轴所围的矩形的面积代表物体的位移为正值;图线与时间轴所围的面积在时间轴的下方表明物体的位移是负值。
二、匀变速直线运动的位移
1.利用v-t图像求位移
2.匀变速直线运动位移与时间的关系式:
[判一判]
(1)物体运动的初速度越大,位移越大。( )
(2)物体运动的加速度越大,位移越大。( )
(3)物体做匀加速直线运动时,a取正值。( )
×
×
×
如图所示
■情境导入
探究
匀变速直线运动位移与时间的关系的理解
■归纳拓展
某质点做匀变速直线运动,已知初速度为v0,在t时刻的速度为v,加速度为a。其v-t图像如图所示。
(1)把匀变速直线运动的v-t图像分成几个小段,如图所示。每段位移≈每段起始时刻速度×每段的时间=对应矩形的面积。故整个过程的位移≈各个小矩形的面积之和。
(2)把运动过程分为更多的小段,如图所示,各小矩形的面积之和可以更精确地表示物体在整个过程的位移。
(3)把整个运动过程分得非常细,很多小矩形合在一起形成了一个梯形OABC,梯形面积就代表物体在相应时间间隔内的位移。
如图所示,速度图线和时间轴所包围的梯形面积为
[例1] 一物体做匀减速直线运动,初速度大小为v0=5 m/s,加速度大小为a=0.5 m/s2,求:
(1)物体在前3 s内的位移;
(2)物体在第3 s内的位移;
(3)物体在15 s内的位移。
因此,第3 s内的位移Δx=x3-x2=12.75 m-9 m=3.75 m。
(3)物体匀减速运动到速度为零时所用时间
答案 (1)12.75 m (2)3.75 m (3)25 m
[针对训练1] 2019年12月8日,观众在“冰立方”观看中国青少年冰壶公开赛女子冰壶决赛,如图甲所示。比赛为期6天,男女各10支青少年队伍在“奥运标准”的全新冰面上展开激烈角逐,最终日本札幌队获得男子组第一名,吉林省队获得女子组第一名。如图乙所示,冰壶以速度v垂直进入四个矩形区域沿虚线做匀减速直线运动,且刚要离开第四个矩形区域边缘的E点时,速度恰好为零。冰壶通过前三个矩形的时间为t,试通过所学知识计算冰壶通过四个矩形区域所需的时间。
甲 乙
解析 从A到E的时间为t1,设每个矩形区域的长为l。
答案 2t
探究
匀变速直线运动推论——平均速度
[例2] 一滑雪运动员从85 m长的山坡上匀加速滑下,初速度是1.8 m/s,末速度是5.0 m/s。
求:(1)滑雪运动员通过这段斜坡需要多长时间?
(2)滑雪运动员通过斜坡中间时刻的瞬时速度是多少?
解析 (1)法一 利用速度公式和位移公式求解。
可得a=0.128 m/s2
t=25 s。
法二 利用平均速度公式求解。
答案 (1)25 s (2)3.4 m/s
[针对训练2] 一辆汽车4 s内做匀加速直线运动,初速度为2 m/s,末速度为10 m/s,在这段时间内,下列说法正确的是( )
A.汽车的加速度为4 m/s2
B.汽车的加速度为3 m/s2
C.汽车的位移为24 m
D.汽车的平均速度为3 m/s
答案 C
探究
匀变速直线运动推论——逐差相等
3.应用
[例3] 从斜面上某一位置每隔0.1 s释放一个相同的小球,释放后小球做匀加速直线运动,在连续释放几个后,对在斜面上滚动的小球拍下如图所示的照片,测得xAB=15 cm,xBC=20 cm。试求:
(1)小球的加速度是多少?
(2)拍摄时小球B的速度是多少?
(3)拍摄时xCD是多少?
解析 小球释放后做匀加速直线运动,且每相邻的两个小球的时间间隔相等,均为0.1 s,可以认为A、B、C、D各点是一个小球在不同时刻的位置。
即xCD=2xBC-xAB=2×20×10-2 m-15×10-2 m=25×10-2 m=0.25 m。
答案 (1)5 m/s2 (2)1.75 m/s (3)0.25 m
[针对训练3] 一个向正东方向做匀变速直线运动的物体,在第3 s内发生的位移为8 m,在第5 s内发生的位移为5 m,则关于物体运动加速度的描述正确的是 ( )
A.大小为3 m/s2,方向为正东方向
B.大小为3 m/s2,方向为正西方向
C.大小为1.5 m/s2,方向为正东方向
D.大小为1.5 m/s2,方向为正西方向
解析 设第3 s内、第5 s内位移分别为x3、x5,则x5-x3=x5-x4+x4-x3=2aT2,得a=-1.5 m/s2,负号表示方向沿正西。故选项D正确。
答案 D
探究
根据v-t图像求物体的位移
[例4] 某一做直线运动的物体的图像如图所示,根据图像求:
(1)物体距出发点的最远距离;
(2)前4 s内物体的位移;
(3)前4 s内物体通过的路程。
答案 (1)6 m (2)5 m (3)7 m
[针对训练4] 一质点的v-t图像如图所示,求它在前2 s内和前4 s内的位移。
解析 位移大小等于图线与时间轴t所围成的面积
所以质点在前4 s内的位移
x=x1+x2=5 m-5 m=0。
答案 5 m 0
科学思维之科学推理
【题目示例】
在匀速直线运动中,物体运动的速度不变,因此位移x=vt,这在数值上恰好等于v-t图像中阴影部分的面积,如图甲所示。证明:在初速度为v0、加速度为a的匀变速度直线运动中,如图乙,梯形的面积在数值上等于匀变速直线运动的位移大小;并推导出位移公式(用v0、a、t表示)。
【推理思维】 在匀变速直线运动中,虽然速度时刻变化,但只要时间足够小,速度的变化就非常小,在这段时间内就可以近似地应用匀速直线运动的公式来计算位移,如图甲所示;如果我们把每一小段Δt内的运动看作匀速运动,则矩形面积之和等于各段匀速直线运动的位移之和,显然小于匀变速直线运动在该时间内的位移,但所取时间段Δt越小,各匀速直线运动位移之和与匀变速直线运动位移之间的差值就越小,如图乙所示,当Δt→0时,各矩形面积之和趋近于v-t图线下面的面积,可以想象,如果把整个运动过程划分得非常细,很多小矩形的面积之和就能准确代表物体的位移了,位移的大小就等于图丙所示的梯形面积。
【推理过程】
解析 匀变速直线运动,物体的位移对应v-t图线和时间轴所包围的图像的“面积”。
答案 见解析
【题后感悟】 对于匀变速直线运动位移公式的推理,运用了“无限分割,逐步逼近”的微分思想,在今后学习重力做功与路径的关系中还会用到。此推理方法实质上是微积分思想在高中物理的体现。
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
