人教版数学七年级上册1.2.1有理数课件(共17张PPT)
文档属性
| 名称 | 人教版数学七年级上册1.2.1有理数课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 134.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-09 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
人教版七年级上册
第一章
有理数
1.2.1
有理数
学习目标
1.了解有理数及其相关概念,知道整数和分数所包含的内容。
2.掌握有理数的分类,通过不同角度对有理数进行分类,更加熟练透彻理解有理数。
3.通过对有理数及其相关概念的理解,以及运用不同方法进行有理数分类,培养学生的思维,养成良好的思考问题的能力。
一、知识回顾
问题1:什么是正数?什么是负数?0是正数吗,0是负数吗?
问题2:正数与负数之间具有什么意义?
问题3:你能再举出一些用正、负数表示数量的实例吗?
答案:例如+5,+2.5,0.5我们把这样带有正号的数叫做正数(正号可以省略不写).例如:-3,-2.5,-0.1我们把带有负号的数叫做负数.
0即不是正数也不是负数.
正数与负数表示是具有相反意义.
例如:存入银行1500元,记作+1500元,支出500元,记作-500元.
探究新知
知识点一:有理数及其相关概念
整数:正整数、0、负整数统称整数。
分数:正分数和负分数统称分数。
有理数:整数和分数统称有理数。
总结:有限小数或无限循环小数都可以转化为分数,因此可以把它们都看成分数。
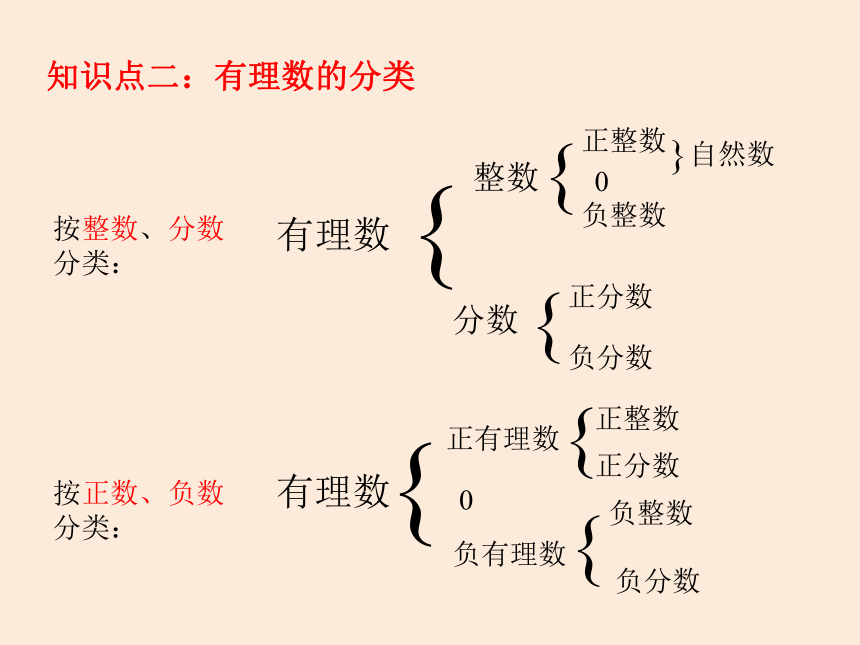
知识点二:有理数的分类
按整数、分数分类:
按正数、负数分类:
{
整数
分数
{
{
正整数
0
负整数
正分数
负分数
}
自然数
{
正有理数
0
负有理数
{
{
正整数
负整数
正分数
负分数
有理数
有理数
温馨提示
1、正数与整数的区别:正数相对于负数而言的,而整数是相对于分数而言的。
2、0既不是正数也不是负数,但它是整数,也是非正数,非负数。
3、数的集合是由所有符合条件的数组成的,它的个数是无限的,所以集合的后面应加上“…”
。如:所有的正数组成正数集合,所有的负数组成负数集合,所有的整数组成整数集合等等。
例1:把下列各数填入相应的集合内:
正数集合
整数集合
负分数集合
非负整数集合
…
…
…
…
正数集合
整数集合
负分数集合
非负整数集合
…
…
…
…
整数集合{
}
分数集合{
}
负分数集合{
}
非负数集合{
}
非正数集合{
}
有理数集合{
}
整数集合{
}
分数集合{
负分数集合{
}
非负数集合{
}
非正数集合{
}
有理数集合
{
}
}
例3:判断题:
(1)零不是整数,也不是正数。
(2)自然数一定是整数。
(3)
一个数,如果不是正数,必定就是负数;
(4)
一个数,不是整数,必定就是分数;
(5)
在有理数中,是负数而不是分数的是负整数;
(6)在有理数中,是整数而不是正数的是负整数。
?
?
?
?
?
?
1.有理数中,最大的负整数是 ;
最小的正整数是 ;
最小的非负整数是 ;
最大的非正数是 ;
最大的负偶数是 .
-1
1
0
0
-2
拓展提升
总结:没有最大的有理数,也没有最小的有理数。
2.判断题:
(1)零是正数.
(2)零是整数.
(3)零是最小的有理数.
(4)
零是非负数.
(5)
零是偶数.
?
?
?
?
?
3.图中两个圆圈分别表示正数集合和整数集合,请分别在图中的三部分中各填入3个数.你能说出这个重叠部分表示什么数的集合吗?
…
…
…
正数
整数
我们知道,有限小数和无限循环小数都属于分数,你能将下列各数转化为分数吗?
课后思考题
课后小结
1、有理数、整数、分数等相关概念
2、有理数的分类
按整数、分数进行分类
按正数、负数进行分类
3、对“0”的认识
4、数的集合以及表示
人教版七年级上册
第一章
有理数
1.2.1
有理数
学习目标
1.了解有理数及其相关概念,知道整数和分数所包含的内容。
2.掌握有理数的分类,通过不同角度对有理数进行分类,更加熟练透彻理解有理数。
3.通过对有理数及其相关概念的理解,以及运用不同方法进行有理数分类,培养学生的思维,养成良好的思考问题的能力。
一、知识回顾
问题1:什么是正数?什么是负数?0是正数吗,0是负数吗?
问题2:正数与负数之间具有什么意义?
问题3:你能再举出一些用正、负数表示数量的实例吗?
答案:例如+5,+2.5,0.5我们把这样带有正号的数叫做正数(正号可以省略不写).例如:-3,-2.5,-0.1我们把带有负号的数叫做负数.
0即不是正数也不是负数.
正数与负数表示是具有相反意义.
例如:存入银行1500元,记作+1500元,支出500元,记作-500元.
探究新知
知识点一:有理数及其相关概念
整数:正整数、0、负整数统称整数。
分数:正分数和负分数统称分数。
有理数:整数和分数统称有理数。
总结:有限小数或无限循环小数都可以转化为分数,因此可以把它们都看成分数。
知识点二:有理数的分类
按整数、分数分类:
按正数、负数分类:
{
整数
分数
{
{
正整数
0
负整数
正分数
负分数
}
自然数
{
正有理数
0
负有理数
{
{
正整数
负整数
正分数
负分数
有理数
有理数
温馨提示
1、正数与整数的区别:正数相对于负数而言的,而整数是相对于分数而言的。
2、0既不是正数也不是负数,但它是整数,也是非正数,非负数。
3、数的集合是由所有符合条件的数组成的,它的个数是无限的,所以集合的后面应加上“…”
。如:所有的正数组成正数集合,所有的负数组成负数集合,所有的整数组成整数集合等等。
例1:把下列各数填入相应的集合内:
正数集合
整数集合
负分数集合
非负整数集合
…
…
…
…
正数集合
整数集合
负分数集合
非负整数集合
…
…
…
…
整数集合{
}
分数集合{
}
负分数集合{
}
非负数集合{
}
非正数集合{
}
有理数集合{
}
整数集合{
}
分数集合{
负分数集合{
}
非负数集合{
}
非正数集合{
}
有理数集合
{
}
}
例3:判断题:
(1)零不是整数,也不是正数。
(2)自然数一定是整数。
(3)
一个数,如果不是正数,必定就是负数;
(4)
一个数,不是整数,必定就是分数;
(5)
在有理数中,是负数而不是分数的是负整数;
(6)在有理数中,是整数而不是正数的是负整数。
?
?
?
?
?
?
1.有理数中,最大的负整数是 ;
最小的正整数是 ;
最小的非负整数是 ;
最大的非正数是 ;
最大的负偶数是 .
-1
1
0
0
-2
拓展提升
总结:没有最大的有理数,也没有最小的有理数。
2.判断题:
(1)零是正数.
(2)零是整数.
(3)零是最小的有理数.
(4)
零是非负数.
(5)
零是偶数.
?
?
?
?
?
3.图中两个圆圈分别表示正数集合和整数集合,请分别在图中的三部分中各填入3个数.你能说出这个重叠部分表示什么数的集合吗?
…
…
…
正数
整数
我们知道,有限小数和无限循环小数都属于分数,你能将下列各数转化为分数吗?
课后思考题
课后小结
1、有理数、整数、分数等相关概念
2、有理数的分类
按整数、分数进行分类
按正数、负数进行分类
3、对“0”的认识
4、数的集合以及表示
